Toiminnallisuutta matematiikkaan

Matematiikassa toiminnallisuudella voidaan tarkoittaa työskentelyä aivan tavallisilla arjen materiaaleilla kuten vaikkapa tikuilla tai helmillä. Esimerkiksi hauskoja tulitikkupulmia löytyy verkosta useita. Toinen toiminnallisuuden lisääjä voivat olla matematiikan oppimisen tueksi suunnitellut toimintavälineet, joita ovat muun muassa murtokakut, geolauta, värisauvat ja multilink-kuutiot. Monia näistä löytyy myös virtuaalisina sivuilta www.didax.com ja www.toytheater.com. Niiden etuina ovat helppo saatavuus verrattuna konkreetteihin välineisiin, ajan säästö, kun opettajan ei tarvitse itse valmistaa materiaaleja, ja motivoivuus. Sitä paitsi yläkouluikäiset saattavat pitää konkreetteja välineitä hiukan lapsellisina.

Toiminnallisuuden lisäämiseksi voimme käyttää myös niin sanottuja historialliskulttuurisia toimintavälineitä kuten helmitaulua. Ja varmasti vielä jostain matematiikan varastoista löytyy laskutikkujakin.

Toiminnallisuutta ovat myös lauta- ja älypelit, erilaiset yhdistely-, lajittelu- ja järjestelykortit sekä leikkelyt, taittelut ja draaman käyttö. Esimerkiksi variaation, permutaation ja kombinaation voi esittää pantomiimina.

Toiminnallisuudella on pitkä historia. Vuonna 1837 saksalainen varhaiskasvatuksen uranuurtaja Friedrich Fröbel aloitti ensimmäisen päiväkotiohjelmansa ja kehitti erilaisia välineitä, joilla päiväkoti-ikäiset oppivat tunnistamaan säännönmukaisuuksia ja geometrisia muotoja. Emme myöskään voi unohtaa italialaista pedagogia Maria Montessoria, joka 1900-luvun alussa kehitti toimintamateriaalien käyttöä ja suunnitteli useita välineitä esikoululaisten ja alakoululaisten matematiikan oppimisen tueksi. Myös monet tutkijat kuten Jean Piaget, Jerome Bruner, Zoltan Dienes, Lev Vygotsky, Richard Skemp ja Paul Cobb esittivät, että lapset tarvitsevat konkreettisia materiaaleja ja piirroksia oppimisensa tueksi ja fyysiset kokemukset ovat myös perusta myöhemmälle abstraktille ajattelulle.

Kahdeksan hyvää syytä käyttää toimintavälineitä

1. Toimintavälineillä kartutetaan käsitteellistä tietoa. Yksittäiset faktat ja ehdot linkittyvät verkostoiksi ja opitaan esittämään arjen tilanteita matematiikan symbolein.  

2. Työskentelyn aikana ehditään ajatella enemmän, kun muistiinpanoja tarvitaan vähemmän.
3. Yhdistely- ja järjestelypelikortteja käytettäessä tarvitaan käänteistä ajattelua eli ”mistä tähän päädyttiin?”
4. Laskuharjoitteita ja toistoja tulee paljon.
5. Matematiikkapuhe lisääntyy, opitaan sanoittamaan ajattelua ja keskustelemaan matemaattisista ideoista ja käsitteistä.
6. Oppimisesta tulee tutkivaa ja kokeilevaa. Opitaan luovaa ajattelua ja eri tapoja ratkaista ongelmatehtäviä tai esittää ratkaisuja.
7. Saadaan apua eriyttämiseen. Heikot oppilaat ja oppilaat, joilla on oppimisvaikeuksia, sekä monikieliset oppilaat saavat lisää tukea oppimiseensa.
8. Opitaan työskentelemään yhdessä. Saadaan omistajuuden kokemuksia ja itseluottamusta omaan matemaattiseen työskentelyyn. Näin myönteiset asenteet lisääntyvät, luokan ilmapiiri paranee, matematiikka-ahdistus vähenee ja oppimisesta tulee hauskempaa.

Toimintamateriaaleilla on monta käyttömahdollisuutta

Toimintamateriaalit tukevat ongelmanratkaisua, päättelyä ja esimerkiksi matemaattista todistamista. Niiden avulla löydetään helpommin säännönmukaisuuksia tai sääntöjä ja rakennetaan yhteyksiä matematiikan eri osa-alueiden välille. Varsinkin avaruudellisen hahmottamisen tueksi ja spatiaalisen muistin kehittämiseen ja hyödyntämiseen ne sopivat mitä mainioimmin. Eikä pidä väheksyä sitäkään, että ne rikastuttavat tai rytmittävät opetusta ja tuovat oppitunneille vaihtelua ja virkistystä.

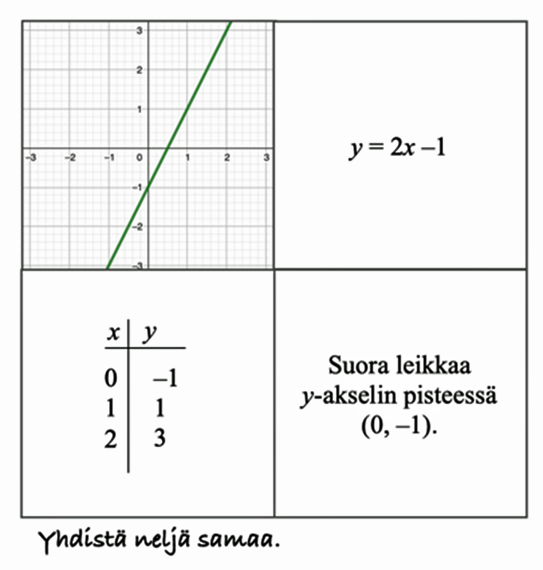
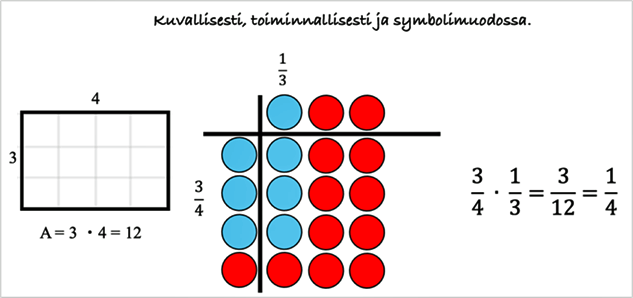
Toiminnallinen, kuvallinen/sanallinen ja abstrakti/symbolinen

Lähestytäänpä sitten murtolukuja, prosentteja, suhteita, todennäköisyyslaskentaa, tilastoja, symmetriaa ja transformaatioita tai geometrisia muotoja, niin usein kannattaa aloittaa toiminnallisin aktiviteetein. Jos oppilaat eivät itse voi käyttää toimintamateriaaleja, on hyvä, että edes opettaja havainnollistaa niiden avulla uutta opittavaa asiaa. Yleensä toiminnallista esitystä kannattaa tukea sanallisin tai kuvallisin esitysmuodoin ja yhdistää mahdollisuuksien mukaan rinnalle symbolinen esitysmuoto.

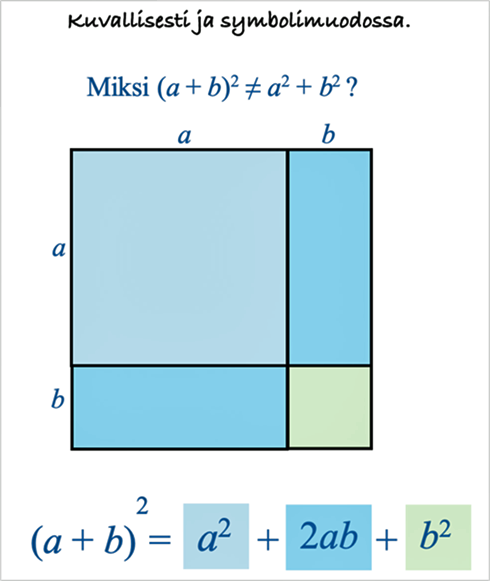
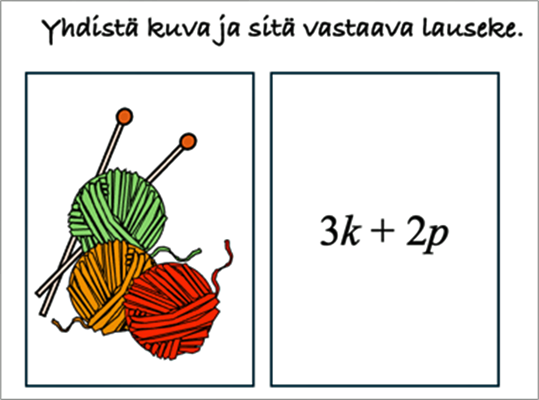
Seuraavissa esimerkeissä on havainnollistettu murtolukujen kertolaskua, lausekkeiden muodostamista, lausekkeen sieventämistä ja yhtälönratkaisua.

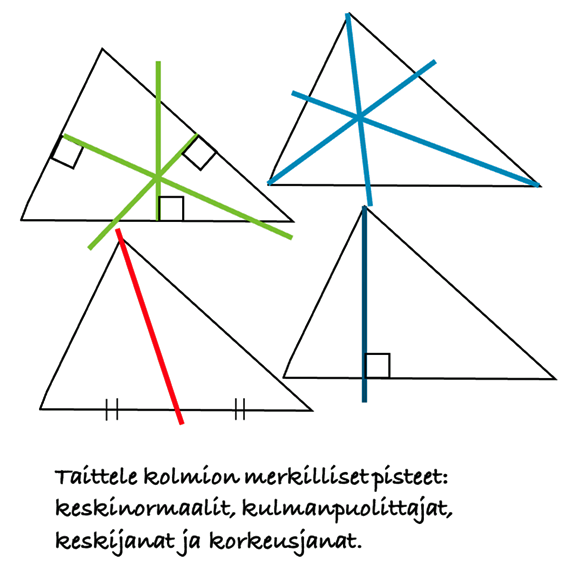
Toiminnallisuuden esteet ovat raivattavissa

Joskus kuulee sanottavan, että opetuksen tavoite on sellainen, ettei toiminnallisuudelle ole tarvetta. Tämän esteen raivaaminen käy helposti.

Jos tavoitellaan menetelmällisiä taitoja ja halutaan lisätä mekaanista harjoittelua, niin toiminnalliset menetelmät ovat siinä parhaimmillaan. Niissä joutuu tekemään useita toistoja. Jos taas pitäisi kiirehtiä opetuksessa eteenpäin ja tavoitteina ovat tiedon ja ymmärryksen lisääminen, niin toiminnallisesti päästään nopeammin ymmärrykseen kuin esittävällä opetuksella. Jos taas halutaan vaikuttaa asenteisiin ja myönteisiin kokemuksiin, niin toiminnallisuudella niihin päästään varmasti.

Toinen hyvin tavallinen este ovat tila, materiaalit ja välineet. Tähän auttaa, jos sijoittelee pulpetit hiukan uudella tavalla, vähentää pikkuisen opettajalle kuuluvaa työtilaa ja uudistaa materiaaleja vähitellen. Pelikortteja voi valmistaa pikkuhiljaa, ja välineitä kuten käyttämättömäksi jääneitä legoja, saattaa löytyä vaikkapa kollegoilta. Oppilaiden sijoittumista tilaan voi myös hiukan pohtia uudelleen.

Kolmas este ovat oppilaat. On totta, että he ovat usein konservatiivisempia kuin opettaja. Toiminnallisuuteen täytyy siis hiukan totutella. Oppilaiden kehitystaso, aikaisemmat tiedot, taidot ja kokemukset vaikuttavat siihen, millaisia valmiuksia heillä on työskennellä toiminnallisesti ja ylipäätään yhdessä. Nämä taidot ovat kuitenkin sellaisia arjen taitoja, ettei niiden harjoitteleminen ole turhaa.

Neljäs usein esille tuleva este on ryhmän koko. Jos pienryhmien tuloksista halutaan keskustella, pienryhmiä ei voi olla kovin monta. Toisaalta pienryhmät eivät voi olla 3-4 oppilasta suurempia. Koonti kannattaakin miettiä tarkkaan ja panostaa erityisesti niihin matemaattisiin oivalluksiin, joita tehtävällä tavoiteltiin.

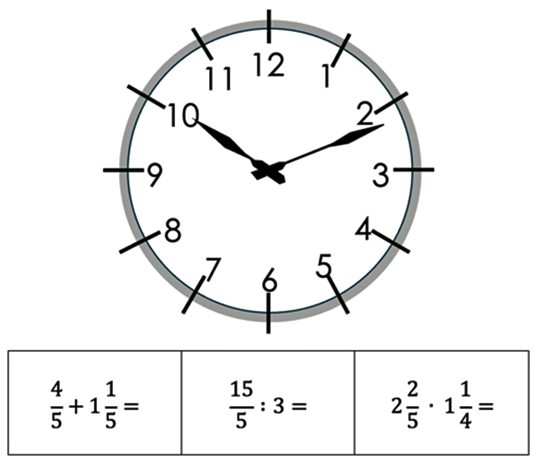
Viidenneksi jätin kaikkein useimmin esille tulevan esteen. Se on aika. Monesti kuulee sanottavan, ettei toiminnallisuuteen ole aikaa. Mutta verrataanpa kahta erilaista oppituntia. Toisella tehdään 30 minuuttia harjoituksia oppikirjasta ja toisella tehdään 15 minuuttia toiminnallisesti ennen harjoittelua, niin luulenpa, että useampia toistoja tehtiin tällä jälkimmäisellä oppitunnilla. Esimerkiksi kellotehtävän avulla tulee tehtyä jo 12 pientä tehtävää.

Lopuksi

Elämyksellisten ja toiminnallisten työtapojen käyttö edellyttää, että opettaja on itse saanut niistä myönteisiä kokemuksia joko ryhmän jäsenenä tai ohjaajana. Lisäksi monet työtavat edellyttävät hyvää aineenhallintaa ja uuden työtavan harjoittelu vaatii sitkeyttä ja pitkäjännitteisyyttä. Ryhmätyöskentelyn ohjaaminen on myös vaativa työtapa. Joku väsyy hälinään, toinen työskentelyn hitauteen ja kolmas heikkoihin tai vain erilaisiin tuloksiin. Silti kannustan kaikkia kokeilemaan. Toiminnalliselta oppitunnilta lähtevät hymyillen pois sekä oppilaat että opettajakin.