Virhekäsityksistä Kenguru-matematiikkakilpailussa

Kenguru-matematiikkakilpailu on yksi maailman suurimmista kansainvälisistä matematiikkakilpailuista. Suomessa kilpailuun osallistuu noin 15000 oppilasta vuosittain aina kakkosluokkalaisista lukiolaisiin asti. Yhdessä Anne-Maria Ernvall-Hytösen ja Mika Koskenojan kanssa tutkimme Kenguru-matematiikkakilpailussa esiintyviä virhekäsityksiä.

Tässä tekstissä virhekäsityksellä viitataan väärinymmärrykseen siitä, miten käsitteet ja ongelmat linkittyvät toisiinsa, eli väärinymmärrykseen käsitteellisen tiedon osalta (ks. esim. Durkin & Rittle-Johnson, 2015; Van Dooren et al., 2015). Virhekäsitysten tutkiminen on tärkeää, sillä niitä tarkastelemalla voi löytää eri tekijöitä, jotka vaikuttavat matemaattisen ajattelun kehittymiseen (Bransford et al., 2000).

Yhdessä Mika Koskenojan ja Anne-Maria Ernvall-Hytösen kanssa tutkimme Suomen Kenguru-matematiikkakilpailussa esiintyviä virhekäsityksiä (ks. Palojärvi et al., 2023). Kenguru-kilpailu on yksi maailman suurimmista kansainvälisistä matematiikkakilpailuista, ja siihen ottaakin Suomessa osaa noin 15000 oppilasta vuosittain kakkosluokkalaisista lukiolaisiin asti. Kilpailu on ilmainen ja avoinna kaikille kouluille, mutta vaatii rekisteröitymisen. Kukin maa kokoaa oman tehtäväsarjansa, joten tehtävät voi valita koulujärjestelmään sopiviksi.

Kenguru-kilpailun tehtävät vaativat sekä matemaattista lukutaitoa, tietämystä että oivaltamista. Esimerkiksi vuoden 2019 6.-7.-luokkalaisten sarjassa oli seuraava kysymys:

”Jere ja hänen kahdeksan serkkuaan ottivat selfieitä. Jokainen näistä serkuista esiintyy kahdessa tai kolmessa valokuvassa. Jokaisessa kuvassa on täsmälleen 5 hänen serkkuaan. Kuinka monta selfietä Jere otti?”

a) 7  b) 6  c) 5  d) 4  e) 5

Yksi mahdollinen tapa ratkaista tehtävä on, että ensin havaitsee serkkujen lukumäärän kuvissa olevan jaollinen viidellä, kun siis lasketaan mukaan kunkin serkun kaikki esiintymiset. Kun sitten tutkitaan erilaisia mahdollisuuksia sille, kuinka moni serkuista saattoi esiintyä kahdessa ja kuinka moni kolmessa kuvassa, jotta tulokseksi tulisi viidellä jaollinen määrä serkkuja yhteensä kuvissa, päädytään, että oikea vastaus on neljä selfietä. Näin ollen tällä ratkaisutavalla tehtävän ratkaiseminen vaatii matemaattista lukutaitoa, sillä tosielämään liittyvä tilanne on laitettava matemaattiseen kontekstiin. Ratkaisija myös hyötyy jaollisuuden ymmärtämisestä, mutta pelkkä määritelmän muistaminen ei riitä tehtävän ratkaisemiseksi.

Esimerkkitehtävän tavoin kaikki tehtävät ovat monivalintaa.

Tutkimuskysymys, data ja tutkimusmenetelmät

Tutkimme kolmea eri kysymystä liittyen oppilaiden mahdollisiin virhekäsityksiin, virheellisiin vastausstrategioihin ja oppilaiden muodostamiin homogeenisiin ryhmiin. Tässä tekstissä keskityn kuitenkin kuvailemaan vain virhekäsityksiin liittyvää tutkimusta, sillä siihen liittyvät tulokset lienevät kaikkein mielenkiintoisimpia.

Tutkimuskysymys kuului seuraavasti: Tarkastellaan sellaisia vastausvaihtoehtoja, jotka ovat tyypillisempiä kuin oikea vastaus. Esiintyykö tällaisessa vastausvaihtoehdossa virhekäsitys ja jos esiintyy, niin mikä?

Virhekäsityksien luokittelua tutkittiin pyrkimällä ratkaisemaan ne tehtävät väärin, joissa jokin muu vastausvaihtoehto kuin oikea oli oikeaa tyypillisempi. Näin pyrittiin rajautumaan vain niihin virhekäsityksiin, joita voidaan sanoa esiintyvän jollain tasolla merkittävissä määrin. Mikäli vähintään kaksi kolmesta tutkijasta oli sitä mieltä, että vastausvaihtoehdossa esiintyy virhekäsitys sekä jakoi saman näkemyksen, mikä virhekäsitys oli, vastausvaihtoehdossa luokiteltiin olevan virhekäsitys. Esimerkiksi vuoden 2015 4.-5.-luokkalaisten sarjan tehtävässä 18 (ks. kuva 1) kysyttiin, kuinka monta neliötä voidaan muodostaa pisteiden välille. Kaikkia muita vastausvaihtoehtoja valittiin useammin kuin oikeaa vastausvaihtoehtoa D, jonka valitsi 10 prosenttia oppilaista. Kaikkein suosituin vaihtoehto oli B; 31 prosenttia oppilaista valitsi sen. Koska vastaukseksi voi saada luvun kolme, jos laskee vain neliöt, joiden sivut ovat yhdensuuntaisia alkuperäisen neliön sivujen kanssa, todettiin tehtävässä olevan mahdollinen virhekäsitys, etteivät neliöt voi olla kuvan tilanteessa vinottain.

Tutkimuksessa käsiteltiin 4-5.-, 6.-7.- ja 8.-9.-luokkien sarjoja, sillä ne olivat osallistujamääriltään suurimpia. Osallistujamäärät vaihtelivat näissä sarjoissa noin 3000 ja 6400 oppilaan välillä. Tarkastelun kohteena olivat vuodet 2011, 2015 ja 2019, sillä ne sisälsivät kaikkien edellä mainittujen sarjojen datan sekä kyseisinä ajankohtina kaikki kilpailijat tekivät kokeen paperisina, jolloin heidän oli mahdollista valita useampi eri vaihtoehto kysymyksiin vastatessaan. Jälkimmäinen ominaisuus oli oleellinen homogeenisiin ryhmiin jakamisen osalta – ei niinkään virhekäsitysten tutkimisen.

Mahdollisia virhekäsityksiä esiintyi eniten geometriassa

Tutkimuksessa löydettiin 24 erilaista mahdollista virhekäsitystä. Näistä puolet liittyi geometriaan, ja monet niistä kuvioiden hahmottamiseen. Esimerkiksi vuonna 2015 4.-5.-luokkalaisten sarjassa esiintyi mahdollinen virhekäsitys, että jos suorakulmaisen, tasakylkisen kolmion hypotenuusan pituus on kaksi, myös kummankin kannan pituus on kaksi. Virhekäsitykset olivat yleisempiä kahdessa nuoremmassa ikäryhmässä kuin vanhimmassa.

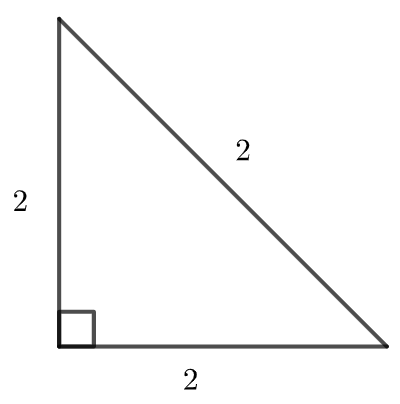
Kuten edellisestä esimerkistä nähdään, virhekäsitysten esiintyminen enemmän nuoremmissa ikäluokissa saattaa osittain selittyä sillä, että myöhemmillä luokka-asteilla opiskeltava teoria voi helpottaa asian ymmärtämisessä. Kun Pythagoraan lauseeseen laittaa kantojen pituuksiksi luvut kaksi, ei hypotenuusan pituudeksi tule kaksi. Tämä ei silti selitä kaikkia virhekäsityksiä tai täysin virhekäsitysten vähenemistä vanhemmissa ikäryhmissä, sillä myös 8.-9.-luokkalaisten sarjassa esiintyi virhekäsityksiä, jotka ovat vastoin heidän näkemäänsä teoriaa. Esimerkiksi vuoden 2011 kilpailussa esiintyi virhekäsitys, että neliön pinta-ala on neljä kertaa sen sivun pituus.

Useimmat virhekäsitykset liittyivät Özeremin (2012) kyproslaistutkimuksen tavoin kuvioiden ja kappaleiden hahmottamiseen. Özeremin tutkimuksessa annetaan suosituksena käyttää enemmän visuaalisia objekteja opetuksessa sekä alleviivata vielä enemmän erilaisten kuvioiden ja kappaleiden yhtäläisyyksiä ja eroavaisuuksia.

Loppusanat

Tutkimuksessa tutkittiin 4.-9.-luokkalaisten virhekäsityksiä Kenguru-kilpailussa. Suurin osa löytyneistä virhekäsityksistä liittyi kuvioiden ja kappaleiden hahmottamiseen. Koska kilpailun tehtävät olivat monivalintaa, ei ole täysin mahdollista nähdä oppilaiden ajattelua ratkaisujen takana, eikä näin ollen varmasti tietää, johtuiko väärä vastaus virhekäsityksestä vai jostain muusta tekijästä. Joissain tutkimuksissa on kuitenkin huomattu, etteivät etenkään nuorimmat suomalaiset oppilaat välttämättä perustele tai selitä omaa vastaustaan edes pyydettäessä, joten on mahdollista, ettei monivalintatehtäviä tarkasteltaessa menetetty merkittävästi tietoa oppilaiden ajattelusta. Monet vastausvaihtoehdot vaikuttivat myös siltä, että ne oli valittu vastaamaan jotain oletettua virheajattelua tai kompastelua ja näin ollen virhekäsitystä. Monivalintakokeiden tutkiminen myös mahdollisti suuren osallistujamäärän tutkimisen.

On myös huomattava, että myös oikean vastauksen takana saattaa olla virhekäsitys (Lobato et al., 2010), joten on mahdollista, että osa virhekäsityksistä jäi löytymättä. Lisää tutkimusta aihepiiristä siis tarvitaan.

Viitteet

Bransford, J. D., Brown, A. L., & Cocking, R. R. (2000). How people learn: Brain, mind, experience, and school. National Academy Press.

Durkin, K., & Rittle-Johnson, B. (2015). Diagnosing misconceptions: Revealing changing decimal fraction knowledge. Learning & Instruction, 37, 21–29.

Lobato, J., Ellis, A. B., Charles, R. I., & Zbiek, R. (2010). Developing essential understanding of ratios, proportions, and proportional reasoning for teaching mathematics: Grades 6–8. National Council of Teachers of Mathematics.

Palojärvi, N., Koskenoja, M., & Ernvall-Hytönen, A. M. (2023). On the Math Kangaroo Finland: Homogeneous subgroups, misconceptions and answering choices. Cogent Education, 10(2).

Van Dooren, W., Lehtinen, E., & Verschaffel, L. (2015). Unraveling the gap between natural and rational numbers. Learning & Instruction, 37, 1–4.

Özerem, A. (2012). Misconceptions in geometry and suggested solutions for seventh grade students. Procedia – Social & Behavioral Sciences, 55(5), 720–729.