Gödelin epätäydellisyysteoreema tekee kvanttikaksoisrakokokeesta epäjohdonmukaisen

Kurt Gödelin epätäydellisyysteoreeman mukaan deterministisesti johdonmukaisen aksiomaattisen järjestelmän sisällä voidaan muotoilla väitteitä, joita ei voida todistaa järjestelmän sisällä. Johdonmukainen järjestelmä on siis epätäydellinen ja vastaavasti täydellinen järjestelmä on epäjohdonmukainen, toisin sanoen, matemaattisen systeemin on aina oltava joko epätäydellinen tai epäjohdonmukainen. 

Gödelin teoreemaa on sovellettu laajasti filosofisen logiikan, tietojenkäsittelytieteen ja fysiikan viitekehyksissä. Alan Turing sovelsi sitä ensimmäisenä laskennan teoriaan. Hän muotoili uudelleen Gödelin teoreeman todistuksen algoritmeilla, jotka suoritetaan hypoteettisella tietokoneella, joka pystyy lukemaan tai kirjoittamaan bitin kerrallaan. Keskeinen havainto oli, että on mahdotonta sanoa, pystyisikö kone suorittamaan laskelmat rajallisessa ajassa. Turing osoitti myös, ettei ole olemassa menetelmää sen osoittamiseksi, päättyykö riittävän monimutkaisen algoritmin suoritus. Nämä rajoitukset koskevat oikeita tietokoneita, koska kaikki tällaiset laitteet vastaavat matemaattisesti Turingin konetta.

David Deutch esitti yhden varhaisimmista kvanttitietokoneen teoreettisista malleista vuonna 1985, kvantti-Turingin koneen, joka on analoginen klassisen Turingin koneen kanssa [1]. Samaan aikaan tutkijat ympäri maailmaa yrittivät soveltaa laskettavuuden teoriaa kvanttifysiikan ilmiöihin. Cubitt työryhmineen käytti kvanttilaskentaa, eli kvantti-Turingin konetta simuloimaan monen kappaleen Hamiltonin laskentaa, saadakseen selville, voidaanko energia-aukon olemassaolo ennustaa [2]. Cubitt kumppaneineen oletti, että ”jos universaali Turingin kone pysähtyy syötteellä n, H(n) on aukollinen, ja jos universaali Turingin kone ei pysähdy syötteellä n, H(n) on aukoton” (eli materiaalilla on jatkuva energiaspektri). 

Tässä työssä pyrimme vastaamaan kysymykseen ”Miten Gödelin epätäydellisyysteoreema liittyy kvanttimekaniikan ristiriitaiseen olemukseen?” Lähestymme kysymystä soveltamalla Turingin koneen pysähtymisongelman todistusta kvanttikaksoisrakokokeen tapauksessa. Kvanttikaksoisrakokoe tarjoaa erinomaisen viitekehyksen työllemme, koska sen löydökset ilmentävät kvanttimekaniikan keskeisiä paradokseja.

Menetelmät ja tulokset

Gödelin ensimmäinen epätäydellisyyslause on analoginen Turingin koneen pysähtymisongelman kanssa. Sen kompakti todistus löytyy Wikipedia-artikkelista. Käytämme todistuksessa funktioita A, A’ ja B sen tutkimiseen, kulkeeko elektroni raon b läpi kvanttikaksoisrakokokeessa. Eisertin ym. mukaan algoritmin päättymättömyys on riippumaton sen fyysisestä toteutuksesta (tai fysikaalisesta teoriasta), toisin sanoen, jos sama algoritmi on päättymätön Turingin koneella, niin se on päättymätön myös kvantti-Turingin koneella ja päinvastoin, koska ne voivat simuloida toisiaan [3]. Toisaalta Deutsch huomautti, että klassisen ja kvanttilaskennan välillä on perustavanlaatuisia eroja, koska kvanttilaskenta hyödyntää kvanttimekaniikan monimaailmatulkintaa siinä missä klassinen laskenta ei sitä hyödynnä [1].

Todistus

Ei ole olemassa sellaista ohjelmaa A, joka pystyisi varmistamaan toisen ohjelman B päättymisen (B:tä käytetään tarkkailemaan, kulkeeko elektroni raon b läpi). Syynä tähän on se, että jos olisi ohjelma A, joka testaa, päättyykö ohjelma B siten, että A(B)=1 (elektroni kulkee raon b läpi) ja A(B)=0, muuten (elektroni kulkee raon a läpi), niin olisi mahdollista kehittää toinen ohjelma A’, joka ei pääty, jos A(B)=1 ja päättyy jos A(B)=0. Nyt kuitenkin A'(A’) päättyy, jos A’ ei pääty (elektroni kulkee raon a läpi) ja ei pääty, jos A’ päättyy (elektroni kulkee raon b läpi).

Todistus osoittaa, että kvantti-ilmiö on klassisesti simuloitumaton; päädytään ristiriitaan. Em. todistuksessa tarkkaillaan vain rakoa b ja gödelinen itseviittaus syntyy siitä, että A’ voidaan ajaa kahteen kertaan A'(A’), jolloin päädytään ristiriitaan (kaksikäsitteinen output). Kaksoisrakokokeelle todistus voitaisiin kirjoittaa myös niin, että funktio A laskisi arvoja B (eli meneekö raosta b) ja funktio A’ laskisi arvoja B’ (eli meneekö raosta a). Tässäkin ajaudutaan ristiriitaan, jos yksi ja sama hiukkanen laukaisee sekä B:n että B’:n, jolloin A ja A’ olisivat samanaikaisesti totta. Tämä on ristiriidassa sen kanssa, että alussa oletetaan, että A ja A’ eivät voi olla samanaikaisesti totta. 

Laskennan vaativuusteoria

Havaintomme voidaan kuuluisan P=NP?-ongelman tavoin yhdistää Eulerin diagrammiksi (Kuva 1). Näin toimimalla saamme kaksi uutta analogiaa. Ensinnäkin kvanttilaskenta ei ratkaise välittömästi P=NP?-ongelmaa (kuvan 1 kaksi puolta voivat olla totta samaan aikaan). Lisäksi yleisesti oletetaan, että P ≠ PSPACE, eli Turingin koneet (TM) ja kvantti-Turingin koneet (QTM) voivat suorittaa PSPACE-luokan tehtäviä polynomisessa tilassa mutta eksponentiaalisessa ajassa (inputin lukuaikaan verrattuna).

Ensimmäinen analogia TM = QTM? on yksinkertaistettu versio kysymyksestä BPP = BQP?, jossa BPP tarkoittaa (sidotun virhetason probabilistista) Turingin konetta. On osoitettu, että BPP sisältyy BQP:hen [4]. 

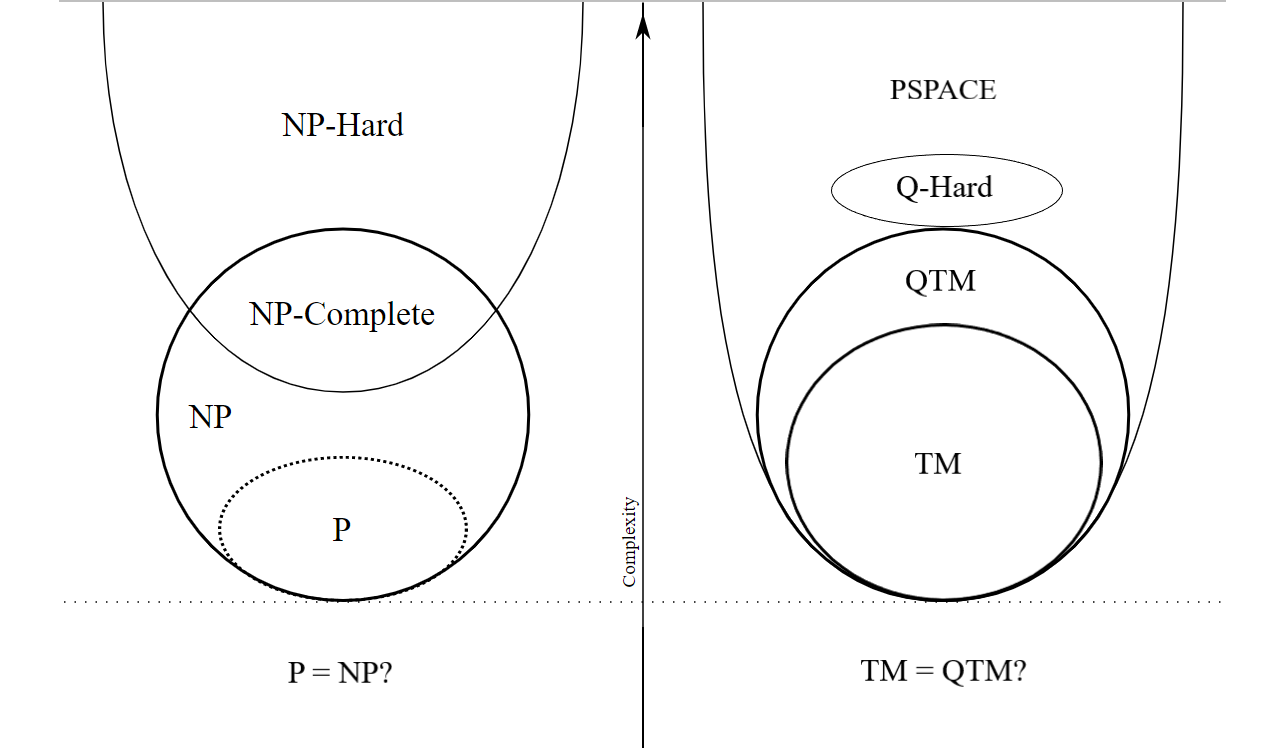
Toiseksi kvanttikaksoisrakokokeen havaittiin muodostavan vaikean tehtävän sekä TM:lle että QTM:lle, ja sijoitimme sen luokkaan ”quantum hard” luokassa PSPACE leikkaamatta TM:ää tai QTM:ää. Deutsch oletti päinvastaista (hän nimesi oletuksensa Church -Turing periaatteen fysikaaliseksi versioksi, jota voidaan kutsua myös CTD-oletukseksi): ”Jokainen äärellinen toteutettavissa oleva fyysinen järjestelmä voidaan täydellisesti simuloida universaalilla tietokoneella äärellisillä keinoilla.” Lisäksi on huomattava, että jos Aharonovin ym. ehdottama DSO-malli (deterministic subset of operators) [5] olisi totta, silloin TM olisi sama kuin QTM. Mielenkiintoisesti myös Stephen Wolfram viittasi tähän suuntaan – hänen versionsa CTD-oletuksesta perustuu klassisesti simuloitavaan kvanttimaailmaan: ”monimutkaiset ilmiöt, joita ei voida pelkistää fysikaalisiin teorioihin, voivat silti olla simuloitavissa” (käyttäen universaaleja soluautomaatteja eli lineaarisia bittikohtaisia operaatioita) [6].

Pohdinta

Turingin koneen käsitettä on käytetty laajasti algoritmisessa informaatioteoriassa, algoritmien monimutkaisuustutkimuksissa, ohjelmistotestauksessa, korkean suorituskyvyn laskennassa, koneoppimisessa, ohjelmistosuunnittelussa, tietoverkoissa ja evoluutiolaskelmissa. Analogiaa Turingin koneen pysähtymisongelman ja kvanttisuperposition välillä ei kuitenkaan ole tehty aiemmin.

Kvanttifysiikan standarditulkinnassa kvanttikaksoisrakokoe yksittäisillä elektroneilla selitetään elektronin paikan epävarmuudella, joka näyttää olevan x-suunnassa, kun taas elektronin liikemäärän (ja nopeuden) epävarmuus on y-suunnassa. Niels Bohr kehitti Kööpenhamina-tulkinnassaan aaltohiukkasdualismista ”komplementaarisuuden”, jossa elektronit voivat olla joko aaltoja tai hiukkasia, mutta eivät samanaikaisesti molempia. Tällöin ei ole järkevää kysyä ”kummasta raosta elektroni kulkee”, koska, kuten tuloksista näemme, se saapuu aaltona rakosysteemiin. Kvanttikenttäteoriassa elektroneja ei pidetä erillisinä hiukkasina, vaan kvanttikenttien yhdistelminä, jotka ovat vuorovaikutuksessa kiinteän rakojärjestelmän synnyttämien kvanttikenttien kanssa tyhjiössä, jolla on myös omat kvanttikenttänsä.

Lisäämme näihin näkemyksiin sen, että kvanttisuperpositio on yksittäisen kvanttimekaanisen hiukkasen perusominaisuus, ja sitä voidaan pitää ”komputaationa”, joka on luonteeltaan ratkaisematon. Sanalla ”komputaatio” tarkoitamme tässä superpositioon liittyvää fysikaalista prosessia, kun taas ”laskennalla” tavanomaista merkitystä, jossa suoritetaan tiettyjä algoritmisia tehtäviä. Tilojen superpositio voi tarkoittaa erilaisia kaksin- tai kolminkertaisia tai moninkertaisia tiloja, kun taas termiä superpositio voidaan käyttää myös makroskooppisesti ”kietoutuneista” tiloista, esimerkiksi tiloista, jotka johtuvat rakojen A ja B lomittumisesta kvanttikaksoisrakokokeessa.

Kvanttimittauksen tulos on tunnetusti ennustamaton. Yhdellä kubitilla voidaan tuottaa satunnaisia binäärisekvenssejä lukemalla sitä toistamiseen. David DiVincenzo listasi seitsemän vaatimusta kvanttilaskennalle ja kvanttiviestinnälle implisiittisellä oletuksella N > 1 [7], mikä tarjoaa meille mahdollisuuden ekstrapoloida kvanttilaskennan käsite yksittäiseen kvanttimekaaniseen hiukkaseen esimerkiksi elektroniin, jonka aaltofunktio on kietoutunut kvanttikaksoisrakokokeen binääriseen (A ja B) rakojärjestelmään. Oletetaan, että mikä tahansa nollasta poikkeava kubittien lukumäärä N ≥ 1 mahdollistaa ”komputaation”. Tällä oletuksella kvanttikaksoisrakokokeen laskennallinen analogia on pelkistettävissä yksittäisen hiukkasen tasolle, kun taas lopullinen simulaatio olisi lineaarinen yhdistelmä matriisioperaatioita yksittäisiin kubitteihin. Yksittäinen kvantti voi olla kahdessa tilassa riippumatta sen bosonisesta tai fermionisesta luonteesta. Tämä on ”komputaation” ainoa vaatimus. Yhden kubitin tapauksessa tämä on implikaatio Wolfgang Paulin kieltosäännöstä (yhtä kubittia voidaan ajatella fermioniparina). Satunnaisuus johtuu ”komputaatiosta”, jossa kubitti on kahta eri energiaa vastaavien tilojen A ja B superpositiossa.

Näkemyksemme kvanttilaskennan käsitteen laajentamisesta tapaukseen N ≥ 1 on sopusoinnussa Cubittin ja kumppaneiden löydösten kanssa; Yksittäinen kvanttimekaaninen hiukkanen on aina ”gapped”. Oma hypoteettinen kvanttilaskennallinen mallimme eroaa Cubittin ja kumppaneiden ”gapped” tapauksesta siinä, että simuloitava suure ei olisi energia vaan olisi intensiteetin paikkajakauma yksidimensionaalisessa rivi-ilmaisimessa.

Willard van Orman Quine esitti esseessään On what there is vuonna 1948 analogian, että Heisenbergin epätarkkuusperiaate fysiikassa vastaa Gödelin epätäydellisyyslausetta matematiikassa. Nykyään, kun kvanttilaskenta on tulossa osaksi teollista tieto- ja viestintäteknologiaa, Heisenbergin epävarmuus ei ole enää ainoa metafora, joka on verrattavissa Gödelin epätäydellisyyteen. Ehdotamme, että termi ”kvantti” sisältää implisiittisesti termin ”laskenta”. Laskennan teoriassa Turingin koneen käsite on laajennettava kvantti-Turingin koneeksi.

Esitämme, että matemaattisen järjestelmän lisäksi myös mikroskooppisen fyysisen järjestelmän eli kvanttisysteemin täytyy olla joko epätäydellinen tai epäjohdonmukainen. Osoitamme, että kaksoisrakokokeen lopputulos on Gödelin teoreeman mukaisesti matemaattisesti ja loogisesti epäjohdonmukainen. Klassinen näkemys hiukkasen liikeradasta näyttää “kiertävän esteen”. Toisaalta interferenssikuvio on täydellinen siinä mielessä, että se on seurausta kokeesta, joka on eristetty tarkkailijasta, eikä järjestelmään tarvitse lisätä mitään (aksioomia Gödelin termein). Tilanne kääntyy päinvastaiseksi, kun rakoja havainnoidaan. Tällöin elektronin havaitaan kulkevan vain yhdestä raosta. Koejärjestelmä on nyt johdonmukainen, muttei täydellinen. Järjestelmä on johdonmukainen, koska havainnot ovat loogisia (elektroni kulkee vain yhdestä raosta). Epätäydellisyys ilmenee interferenssikuvion puuttumisena; superposition toista osapuolta eli elektronia, joka kulkee toisesta raosta, ei ole, jolloin johdonmukainen järjestelmä on alkuperäisen täydellisen järjestelmän puolikas.

Vain harvat tieteelliset tutkimusartikkelit ovat pyrkineet luomaan klassisia tai kvanttilaskennallisia simulaatioita kvanttikaksoisrakokokeesta. Aharonov ja kumppanit väittävät, että Heisenberg-kuvalla on laskennallinen etu Schrödinger-kuvaan verrattuna [5]. Gard työryhmineen puolestaan arvelee, että kvanttiteorian Schrödingerin ja Heisenbergin kuvat, vaikka ovatkin matemaattisesti ekvivalentteja, eivät ole laskennallisesti samanarvoisia [8]. Gard kumppaneineen vertasi bosonisia ja fermionisia tapauksia kvantti-Pachinko-konemallissaan, kun taas Aharonovin ja kumppaneiden DSO-mallissa tarkasteltiin vain fermioneja Heisenberg-kuvassa.

Kvanttilaskennan näkökulmasta ehdotettu ”laskentaetu” Heisenbergin kuvaa käyttämällä jää edellä mainitussa tutkimuksessa näyttämättä. Lisäksi nykyiset universaalit kvanttialgoritmit käyttävät Schrödingerin kuvaa, mikä ei tue käsitystä, jonka mukaan Heisenbergin kuva tarjoaisi edellä mainittua etua. Gardin ja kumppaneiden kvantti-Pachinko-konemalli tarjoaa toistaiseksi parhaan toteutuksen kvanttikaksoisrakokokeen laskennalliselle analogialle. Sekä Aharonov että Gard työryhmineen rakensivat kvanttisimulaatioitaan klassisen Turingin koneen kontekstissa. Aharonov ja kumppanit väittää tekevänsä kaksoisrakokokeesta ”vihdoin järkevän””, kun taas Gard työryhmineen tekee varovaisempia johtopäätöksiä; ”Ei ole tiedossa (mutta on epätodennäköistä), ovatko tällaiset bosoniset interferometrit universaaleja kvanttitietokoneita.”

Laskennan vaativuusteoria

Tässä artikkelissa olemme muotoilleet kaksi uutta analogiaa suhteessa Clay Instituten ”miljoonan dollarin ongelmaan” P = NP? Tämän ongelman kvanttivastine voidaan muotoilla seuraavasti: TM = QTM? kun taas toinen analogia tulee siitä tosiasiasta, että realistiset kvanttisimulaatiot näyttävät olevan vaikeita laskennallisia tehtäviä (analogisesti NP-täydellisten tehtävien kanssa). Kvanttilaskennan puitteissa olemme ottaneet käyttöön luokan ”quantum hard” luokassa PSPACE siinä mielessä, että tulevat kvanttitietokoneet ja algoritmit voivat suorittaa tällaisia tehtäviä, vaikka ne olisivat klassisesti simuloitumattomia (Kuva 1b). Lisäksi Deutsch väittää, että TM ⊂ QTM, mistä seuraisi, että P ≠ NP, koska mikään algoritmi ei lyhennä NP-tehtävän eksponentiaalista laskenta-aikaa enemmän kuin Groverin algoritmi [9]. Tämä algoritmi vähentää sen neliöjuureen eikä logaritmiin, joka tarvittaisiin polynomiajan saavuttamiseksi.

Johtopäätökset

Teoreettisessa fysiikassa matemaattiset totuudet ennustavat fyysistä todellisuutta. Sanomme esimerkiksi, että spiniksi kutsutun elektronin binäärinen kvanttiluku tulee Paulin kieltosäännöstä, jonka mukaan kahden identtisen fermionin kaikki neljä kvanttilukua eivät voi olla samat.

Mutta kertooko Gödelin epätäydellisyysteoreema jotain teoreettisen fysiikan rajoituksista? Tulostemme valossa tämän kysymyksen muotoilua on harkittava uudelleen. Muuttaako kvanttilaskennan ja kvanttifysiikan välinen analogia teoreettisen fysiikan roolin ”digitaalisen fysiikan” algoritmisen monimutkaisuuden tutkimukseksi? Tämä kysymys saattaa olla relevantti laskennallisen fysiikan kontekstissa, mutta se voi jäädä vaille vastausta laajemmassa kontekstissa. Kuten Stephen Hawking [10] huomautti; ”Emme ole enkeleitä, jotka näkevät maailmankaikkeuden ulkopuolelta. Sen sijaan me ja mallimme olemme molemmat osa kuvaamaamme maailmankaikkeutta. Näin ollen fysikaalinen teoria viittaa itseensä, kuten Gödelin lauseessa. Sen vuoksi voisi odottaa sen olevan joko epäjohdonmukainen tai epätäydellinen.” Mielenkiintoisen näkemyksen esitti myös Stephen Wolfram [6], joka oletti, että monet fysikaaliset systeemit ovat laskennallisesti redusoitumattomia, joten niiden oma evoluutio on itse asiassa tehokkain menettely niiden tulevaisuuden määrittämisessä. ”Näin ollen moniin näitä järjestelmiä koskeviin kysymyksiin voidaan vastata vain hyvin pitkillä tai mahdollisesti äärettömillä laskelmilla. Mutta joitain kysymyksiä, joihin voidaan vastata yksinkertaisemmilla laskelmilla, voidaan silti muotoilla.”

Väitämme, että kvanttikaksoisrakokokeen tavoin myös muut kvanttifysikaaliset ilmiöt ilmentävät Turingin koneen pysähtymisongelmaa ja Gödelin epätäydellisyyslausetta. Richard Feynman [11] kutsui kaksoisrakokoetta ”ilmiöksi, jota on mahdoton selittää millään klassisella tavalla ja jossa on kvanttimekaniikan sydän” (eli kvanttisuperpositio). ”Todellisuudessa se sisältää kvanttimekaniikan ainoan mysteerin”. Tämä on sopusoinnussa kvanttikaksoisrakokokeen laskennallisen analogian kanssa, jossa kvanttisuperpositio on yläkäsite ja kvanttilomittuminen on alakäsite.

Tähän asti ei ole ollut selvää yksimielisyyttä siitä, mitä tekemistä Gödelin teoreeman mukaisella itseviittaavuudella on fyysisen todellisuuden tai fysikaalisten teorioiden kanssa. Yksi keskeinen kysymys on, onko kvanttimekaniikassa paradokseja? Se että yksi hiukkanen on kahdessa paikassa samanaikaisesti vaikuttaa paradoksaaliselta, vaikka jotkut tutkijat väittävät, että se johtuu vain siitä, että itsepintaisesti haluamme käsittää hiukkaset erillisinä partikkeleina emmekä aaltoina.

Monet teoreetikot, mukaan lukien Albert Einstein ja David Bohm, uskoivat, että kvanttimekaniikan paradoksit katoavat ajan myötä. Heillä oli visio klassisesti deterministisesta maailmasta, ja he toivoivat, että täydellisempi teoria tekisi myös kvanttimekaanisesta maailmasta deterministisen. Jaamme Hawkingin indeterministisemmän näkemyksen, jonka mukaan ”olemme määrittäneet determinismin uudelleen, ja se on vain puolet siitä, mitä Laplace ajatteli sen olevan.” Gödelin epätäydellisyyslause luo paradoksin matematiikan ytimeen. Turingin koneen pysähtymisongelman todistuksen avulla löysimme analogian Gödelin teoreeman ja kvanttikaksoisrakokokeen välillä. Siten olemme yhdistäneet sen fysikaaliseen todellisuuteen.

Viitteet:

[1] DEUTSCH D., Proc R Soc Lond A Math Phys Sci., 400 (1985) 97-117. https://doi.org/10.1098/rspa.1985.0070

[2] CUBITT T. S. et al., Nature., 528 (2015), 207-211. https://doi.org/10.1038/nature16059

[3] EISERT J. et al., Physical review letters., 108 (2012) 260501. https://doi.org/10.1103/PhysRevLett.108.260501

[4] BERNSTEIN E. and VAZIRANI U., Quantum complexity theory. Society for Industrial and Applied Mathematics Journal of Computation. 26 (1997) 1411-1473.

[5] AHARONOV Y. et al., Proc of the Nat AS., 114 (2017), 6480-6485. https://doi.org/10.1073/pnas.170464911

[6] WOLFRAM S., Physical Review Letters., 54 (1985) 735-738.

[7] DIVINCENZO D. P., Fortschritte der Physik: Progress of Physics, 48 (2000), 771-783. https://doi.org/10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E

[8] GARD B. T. et al., Physical Review A., 89 (2014), 022328. https://doi.org/10.1103/PhysRevA.89.022328

[9] GROVER L., A fast quantum mechanical algorithm for database search, in Proc. 28th Annual ACM Symposium on Theory of Computing (ACM, New York) 1996, pp. 212-219.

[10] HAWKING S., Gödel and the End of Physics. See http://www. hawking. org. uk/index. Php/lectures/91.

[11] FEYNMAN R. P. et al., American Journal of Physics., 33 (1965) 750-752. https://doi.org/10.1119/1.1972241