Matematiikkaa senioreille

Matematiikka ei ole vain kouluaine ja monen toimialan työväline. Se kelpaa aivoja virkistäväksi harrastukseksi seniori-ikäisillekin. Koulumatematiikka ei ole tähän aikanaan valmistanut eikä kannustanut, joten tarvitaan innostava ohjaaja. Hannele Ikäheimo ryhtyi toimeen ja perusti toiminnallisen matematiikan työtapoihin nojautuvan aivojumppakerhon. 

Hannele Ikäheimo on pitkän linjan matematiikan opettaja, kouluttaja ja tietokirjailija. Dimension lukijoille hän ja hänen tekemisensä ovat tuttuja muutamista artikkeleista ja kirjaesittelyistä, esimerkiksi Kolme oppilastapausta 3.2.2022, Matematiikan osaaminen vahvaksi 27.2.2021, Allvar-palkinto matematiikan opettajalle (Dimensio 4/2017), Kymmenjärjestelmä – matematiikan osaamisen kulmakivi (2/2013), Oppimisen iloa – Nean matikka (1/2013), Matikkamaa – Mattelandet (1/2003). 

Hannele muutti Munkkiniemen Saga-palvelutaloon kahdeksankymppisenä tammikuussa 2024 lapsuutensa ja vanhuutensa maisemiin. Talossa asuu kolmisensataa seniori-ikäistä. Lisäperusteena asuinpaikan valinnalle oli, että talon johto suhtautui hyvin myönteisesti hänen ideaansa matematiikkakerhon pitämisestä. 

Keskustellessaan ajatuksestaan etukäteen joidenkin asukkaiden kanssa Hannele sai kuulla, että kukaan ei varmaankaan tule suureen saliin kuuntelemaan ”esitelmää” matematiikasta. Lisäksi jo pelkkä sana ”matematiikka” saattaa säikyttää monia ja estää osallistumisen. Ei siis perustettu matematiikkakerhoa, vaan harrastusta mainostettiin aivojen virkistämisenä, aivojumppana. Eikä kyse ole pelkästään tilapäisestä virkistyksestä, vaan aivoterveyden ylläpitämisestä, sillä aivot toimivat kuten lihakset: jos niitä ei käytä, ne alkavat surkastua.

Kesällä 2024 kerrottiin ideasta talon asukkaille viikkotiedotteessa näin: ”Aivojumppaa Sagan asukkaille. Tule kokeilemaan, miten loogista ajattelua voidaan kehittää värikkäiden muovinpalojen avulla. Yhdessä asukkaamme Hannele Ikäheimon kanssa saadaan yllättäviä ja iloisia kokemuksia.”

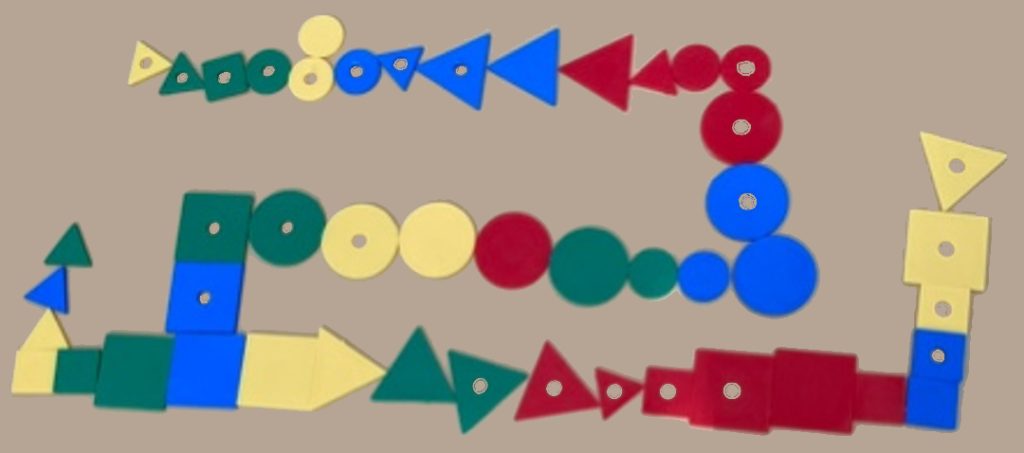
Ensimmäiselle tapaamiskerralle elokuun alkupuolella 2024 tuli seitsemän uteliasta. Aloitettiin tekemällä ja selostamalla tekemistä ääneen. Välineenä olivat loogiset palat, joiden ominaisuuksia ovat koko, muoto, väri ja reikäisyys. Ensiksi tarkasteltiin paloja yksittäin. Minkä värinen se on? Onko se iso vai pieni? Mitä muotoja on? Kuinka monta vaihtoehtoa on kussakin ominaisuudessa? 

Yksinkertainen perusharjoitus on koota ketju, jossa vain yksi ominaisuus vaihtuu palasta toiseen. Osallistujien taidot olivat hyvin erilaiset, mutta monet totesivat, että tämä on mielekästä ja ajattelua kehittävää työskentelyä. Ja luovuuttakin sai käyttää. Jos ei löytynyt sopivaa palaa ketjun päähän, niin sai lisätä haaroja.

Toisella kerralla mukana oli jo kymmenen osallistujaa. Nyt tutustuttiin murtokakkuihin, ympyrälevyihin, jotka on jaettu tasaosiin: yksi kokonainen, kaksi puolikasta, kolme kolmasosaa, neljä neljäsosaa jne.

Ensimmäisenä tehtävänä oli yksinkertainen vertailu. Fläppitaululla merkinnät 1/6 ja 1/3. Kumpi on suurempi? Konkreettisesti toiseen käteen kuudesosa ja toiseen kolmasosa. 

Tunnelma oli iloinen ja ihmettelevä. Voiko matematiikka olla tällaistakin. ”Tämän voi nähdä! Tämän voi jopa tuntea!” Käsitys matematiikasta alkoi muuttua. ”Tämä on niin erilaista kuin koulussa minun aikanani! Tätä konkretiaa olisin tarvinnut, kun en ymmärtänyt, vaan opettelin aina ulkoa säännön.”

Yritettiin tutustua myös SUMU-peliin (suurin murtoluku), mutta se ei ottanut tulta. Pelaaminen lukukorteilla oli liian sekavaa eivätkä luvutkaan tuntuneet niin konkreettisilta kuin murtokakut, vaikka peli toimiikin alakoululaisten kanssa. Tekemisen välissä syntyi kuitenkin monenlaista keskustelua matematiikkamuistoista. Moni kertoi matematiikka-ahdistuksestaan. 

Kolmannella kerralla vertailtiin monimutkaisempia murtolukuja murtokakkujen avulla, esimerkiksi 2/3, 3/2 ja 1 1/2. Suurta ihmetystä! Työskentely SUMU-pelikorteillakin toimi paremmin, kun osallistujat toimivat pareittain. Koko tunti samaa aihetta alkoi kuitenkin tuntua raskaalta. Toivottiin vaihtelua. Ehkä kaksi eri aihetta ensi kerralla, kumpaakin puolet ajasta.

Neljännellä kerralla olikin sitten käytössä sekä murtokakkuja että linkkikuutioita. Fläppitaululla tarjottiin virheellisiä laskusuorituksia. Tehtävänä oli esittää laskut murtokakuilla ja etsiä oikeat tulokset. 

1/3+1/3= 2/6

2∙1/5=2/10    

3/6:3= 1/2    

Ymmärrystä haettiin myös sanoittamalla tehtäviä, esimerkiksi viimeinen edellä mainituista näin: ”Kolme kuudesosaa jaetaan kolmelle henkilölle tasan! Kuinka paljon kukin saa?” Menetelmän toimivuutta osoittaa osallistujan palaute: ”Jos minulla olisi ollut koulussa tai nyt pelkkä lasku, en olisi osannut laskea. Nyt, kun on nuo murtokakut ja kun lasku myös sanoitettiin, niin ymmärsin!” Toinen kommentti: ” Me ollaan hyviä!” Sitten tehtiin omia laskuja murtokakuilla. Ne sanoitettiin ja kirjattiin näkyviin luvuilla.  

Linkkikuutiot ovat toisiinsa liitettäviä, värillisiä muovikuutioita; paljon käytetty toiminnallisen matematiikan opetusväline, sopii monenlaisiin tarkoituksiin. Niillä opeteltiin ohjeiden antamista ja toimimista ohjeiden mukaan. Parin kummallekin jäsenellä on viisi eri väristä kuutiota, kummallakin samat värit. Niitä liitettiin toisiinsa ohjeen mukaan. Toinen tekee ja antaa ohjeita toiselle. 

Ensin istuttiin vierekkäin niin, että ohjeiden vastaanottaja näki, mitä ohjeiden antaja teki antaessaan ohjetta. Tämä vaihe tuntuu ehkä liiankin helpolta, mutta ohjeen antamista oli tarpeen harjoitella, sillä ”matikassa ei yleensä puhuta”, sanoo Hannele. Kun kumpikin oli harjoitellut, käännyttiin selät vastakkain ja jatkettiin samoin. Ohje saattoi alkaa näin: ”Ota keltainen kuutio, laita punainen sen oikealle puolelle.” Lopuksi verrattiin rakennelmia toisiinsa. Tuliko samanlainen?

Viidennellä kerralla jatkettiin linkkikuutioilla. Tehtiin monimutkaisempia rakennelmia kuin edellisellä kerralla. Lopputunnista otettiin mukaan ruutupapereita ja värikyniä. Piirrettiin rakennelmista perspektiivikuvia eri suunnista katsottuna.

Kuudennen kerran aiheena olivat mittaaminen ja mittayksiköt. Aloitettiin perushahmotuksesta eikä ulkoa opeteltavista yksiköiden luetteloista ja etuliitteistä, esimerkkinä pituuden mittaamisen konkreettiset tukipisteet. Niitä esitettiin omien käsien ja sormien avulla kuvamallin mukaan ensin suurimmasta pienimpään ja sitten päinvastoin. Lopuksi silmät kiinni tehtynä tämä sekä nauratti että ihmetytti.

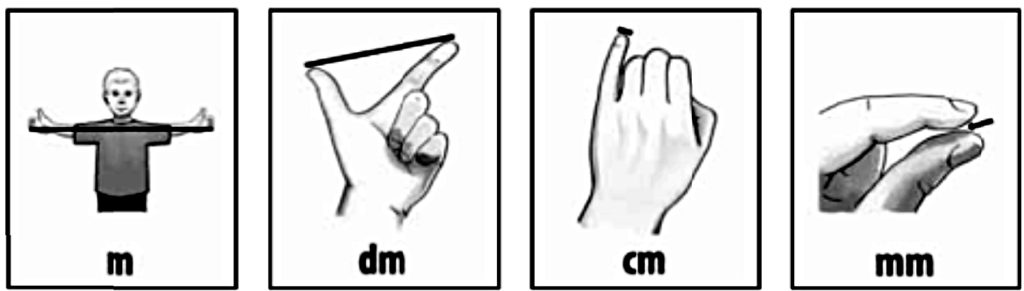
Yksiköihin tutustuttiin tarkemmin mittayksikkökorttien avulla. Niitä on kaikkiaan 181: pituus, massa, litratilavuus, pinta-ala ja kuutiotilavuus. Koska korttien käyttö oli osallistujille uutta, käytettiin niiden pohjana monistetta, jolle kortit asetettiin. Tämä helpotti työskentelyä ja kaikki innostuivat tästä työskentelystä. ”En ole tätä ennen ymmärtänyt!” ”Tämä pitää minun opettaa lapsenlapsilleni!” 

Hannele oli hämmästynyt, että tunnin aikana saatiin kaikki kortit järjestykseen 3–4 hengen ryhmissä. Tähän aiheeseen kannattaa palata myöhemmin! Kirjassa Matematiikan osaaminen vahvaksi Hannele on tarkkaan kuvannut mittayksikkökorttien käyttöä. Niistä on myös selittäviä Youtube-videoita, esimerkiksi https://urly.fi/3SNA. Sivulla on linkkejä muihinkin videoihin. 

Seitsemännellä kerralla tehtiin myös fyysistä aivojumppaa VIRE-ohjelmaa mukaillen https://peda.net/haapavesi/se/tunnekasvatus/menetelmi%C3%A4/aivojumppa. Siinä on yksinkertaisia liikkeitä, joiden on havaittu lievittävän stressiä, rentouttavan ja rauhoittavan. Yksityiskohtaisempia ohjeita on Suomen kinesiologiayhdistys ry:n vuonna 2005 kustantamassa Aivojumppa-oppaassa.

Jatkettiin loogisilla paloilla. Tehtiin jonoja, joissa palasta toiseen vaihtuu tasan kaksi ominaisuutta. Vaikeampana tehtävänä oli rakentaa kaksiulotteinen asetelma, jossa oikealle edettäessä (kullakin rivillä) vaihtuu palasta toiseen tasan yksi ominaisuus ja alas edettäessä (sarakkeessa) vaihtuukin kaksi ominaisuutta.

Vertailtiin tilavuuden yksiköitä. Kuutiometri vie ison tilan pöydälle asetettuna. Sen sisään mahtuisi jopa istumaan. Sen sijaan kuutiosenttimetri on tuskin havaittavissa samassa kuvassa. Kuutiodesimetrejä ja -senttimetrejä voisi käyttää myös rakennuspalikoina. Niitä vain tarvittaisiin valtavan paljon, jos haluttaisiin rakentaa kuutiodesimetri kuutiosenttimetreistä, puhumattakaan kuutiometrin kokoamisesta.  

Oli aloitettu elokuussa. Nyt oltiin jo joulun alla. Kaikki halusivat jatkaa uuden vuoden puolella. 

Kahdeksas tapaamiskerta oli heti tammikuun alussa 2025. Aiheena oli mayaintiaanien lukujärjestelmä. Se on 20-kantainen paikkajärjestelmä. Numeromerkkejä on lukumäärille ’yksi’, ’viisi’ ja ’nolla’. Niitä edustamaan käytettiin papuja, tikkuja ja simpukoita. Aihetta ei lähestytty paikkajärjestelmän suunnasta, vaan tarinoiden ja esimerkkien avulla, esimerkiksi niin, että kirjattiin pellolta haettujen maissintähkien lukumääriä. Opeteltiin merkitsemään lukuja lukualueella 0–20 ja tehtiin helppoja yhteen- ja vähennyslaskuja.  Kuvan luvut ovat 4, 7, 11 ja 20. Osallistujat kommentoivat aihetta näin: ”Kovaa aivojumppaa… ei liian vaikeaa, mutta kuitenkin vaativaa.”

Yhdeksännellä kerralla oli useita aiheita. Kerrattiin pienten lukujen esittäminen mayojen lukujärjestelmässä ja tehtiin muutamia yhteen- ja vähennyslaskuja pienillä luvuilla. Sitten rakennettiin suurempia lukuja kymmenjärjestelmän luvuista 20, 40, 60, 80, 100, 200, 201, 202, 400. ”Nyt on aivoissa paljon liikettä, todellista aivojumppaa!” Ei ollut liian vaikeaa. Joillekin paikkajärjestelmän idea meni vielä yli ymmärryksen, toisille se oli ihan ymmärrettävää.

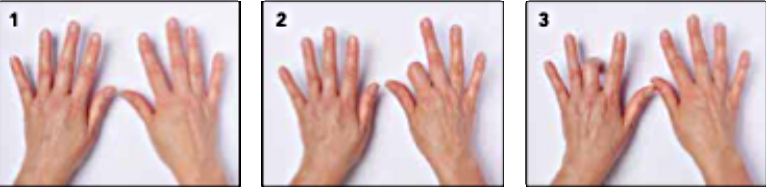
Yhdeksän kertotaulua opeteltiin sormia käyttäen, kuvassa 7 ⋅ 9 (osakuva 2) ja 3 ⋅ 9 (osakuva 3). Tuloksen kymmennumero näkyy taivutetun sormen vasemmalle puolelle ja ykkösnumero oikealle puolelle jäävien sormien määrästä. Ällistystä: ”Miten tämä on mahdollista?” Vastaus ”meillä on kymmenjärjestelmä” ei kertonut osallistujille mitään, vaan aiheutti jatkokysymyksen: ”Mikä se on?” Lisää esimerkkejä ja keskusteluohjeita on kirjassa Matematiikan osaaminen vahvaksi s. 276–279.

Kymmenjärjestelmään tutustuttiin opetusrahojen ja TSKY-paikka-alustan (tuhannet–sadat–kymmenet–ykköset) avulla (emt. s. 145–146). Kuinka monta yhden euron kolikkoa tarvitaan, että saadaan 10 euron seteli? Kuinka monta 100 euron seteliä tarvitaan 1000 euron seteliin? Mitkä rahasummat ovat kuvissa?

Kymmenjärjestelmää voidaan havainnollistaa myös eripituisilla helminauhoilla, esimerkiksi kymmenjakoinen satanauha tai tuhatnauha, joiden idea on alun perin peräisin Montessori-pedagogiikasta. Helminauha saattaa tuntua kovin yksinkertaiselta välineeltä matematiikan oppimiseen ja harrastamiseen, mutta elämys voi olla vahva, mitä kuvaa alakouluikäisen tytön toteamus: ”Ei pelota tuhat enää”. Tarina sisältyy edellä mainitun teoksen esittelyyn (Dimensio 27.7.2021).

Kymmenennen kerran aluksi syvennettiin ymmärrystä kymmenjärjestelmästä opetusrahojen avulla. Fläppitaululla oli lukuja, joita rakennettiin TSKY-alustalle. Lukuja laskettiin yhteen, vähennettiin, kerrottiin kahdella ja jaettiin sekä ositus- että sisältöjakona. Ihmeellisin oli lasku 6000 – 123 rahoilla. Rahojen käyttö ja laskujen sanoittaminen tarinoiksi konkretisoivat ositus- ja sisältöjaon eroa: 20 € : 2 = 10 €, mutta 20 € : 2 € = 10. 

Tilanteen innostavuutta kuvaa seuraava keskustelu:

Marjukka: ”Minä olen pitänyt itseäni hyvänä matematiikassa, mutta nyt päästä tulee savua!”
Hannele: ”Sattuuko?”  
Marjukka: ”Ei, mutta tämä on niin erilaista ja mielenkiintoista!”

Lopuksi tutustuttiin geometrisiin paloihin. ”Mitä me tehdään näillä?” ”Saatte keksiä ihan itse!” ”Sitten tehdään murtolukuja.”

Yhdennellätoista kerralla tutkittiin, miten geometrisillä paloilla voidaan havainnollistaa murtolukuja. Tämä oli vaikeampaa kuin ympyränmuotoisilla murtokakuilla. Ohjaajaakin ihmetytti, miten innokkaasti kaikki ryhtyvät työskentelemään alkuohjeiden jälkeen pienissä ryhmissä. Lopuksi ratkottiin sheikin aarrearkkujen perinnönjakotehtävää (kirjasta Murtolukuja välineillä luokille 3–9 s. 49) murtokakuilla, värinapeilla ja laskemalla yhtälön avulla. Tämän ratkominen kiehtoi, koska se vaikutti aluksi hyvin vaikealta, mutta pian huomattiin murtokakkujen vahvuus ymmärtämisessä.

Kahdennellatoista kerralla tehtiin kuvioita 11×11-piikkiselle geolaudalle ja pohdittiin kuvioiden nimityksiä nelikulmio, neliö, neljäkäs, suunnikas, monikulmio jne. sekä niiden suhteita. Tekeminen oli hauskaa. Muutamat hihkuivat: ”Tämä sopii minulle!” Geolaudalle tehtyjen kuvioiden piirtäminen paperille on kokemuksen mukaan sekä kiehtovaa että haastavaa ja hahmottamisen kannalta tärkeä vaihe.

Kolmannellatoista kerralla jatkettiin työskentelyä sekä 5×5- että 11×11-geolaudalla ohjemonisteen mukaan. Pareittainkaan tekeminen ei kaikilta onnistunut niin hyvin kuin Hannele oli odottanut.

Kivaa oli kuitenkin.

Neljännellätoista kerralla palattiin kertotauluihin. Tutustuttiin noppien avulla siihen, mitä kertolasku tarkoittaa.  Ihmetystä herätti, kun nopilla tehtiin laskut 2 · 5 = 10 ja 5 · 2 = 10 (kuva). ”Tulos on sama, mutta ne näyttävät ihan erilaisilta! En ole tätä ennen nähnyt!” Monia muitakin kertolaskuja esitettiin nopilla. 

Kertotauluja ei ole välttämätöntä opetella vanhaan tapaan kokonaisina, vaan riittää osata muutamat tukipisteet: kertomiset yhdellä, kahdella, viidellä ja kymmenellä. Muut tulokset saadaan yhteen- tai vähennyslaskulla, esimerkiksi 6 ⋅ 5 saadaan lisäämällä yksi viitonen tukipisteeseen 5 ⋅ 5 = 25 ja vastaavasti 9 ⋅ 5 vähentämällä 5 tukipisteestä 10 ⋅ 5 = 50. Tätä harjoiteltiin pienissä ryhmissä suullisesti. Tarkemmin tukipisteistä koostuvien lyhyiden kertotaulujen opettelusta on kerrottu Matematiikan osaaminen vahvaksi -kirjassa (s. 271–275).

Viidennellätoista kerralla palattiin loogisiin paloihin. Arvuuteltiin, mikä pala on piilossa, tekemällä kysymyksiä, joihin voi vasta vain kyllä tai ei. Ensin muutama kerta kaikkien kanssa yhdessä, sitten pienissä ryhmissä.  Hyvin meni! Sitten tehtiin pitkiä ketjuja, joissa vaihtui yksi ominaisuus palasta toiseen, vaikeammassa muunnelmassa tasan kaksi ominaisuutta. Ketjuista tuli pitkiä: 40 palaa ja ylikin. Vielä vaikeampi harjoitus oli tehdä kaksiulotteista kuviota, jossa oikealla edettäessä vaihtui yksi ominaisuus ja alaspäin edettäessä kaksi ominaisuutta. ”Vaikeaa. Halutaan tehdä vielä ensi kerralla!”

Loogiset palat olivat esillä vielä kuudennellatoistakin kerralla. Tehtiin vielä ketjuja ja kaksiulotteisia rakennelmia samoilla säännöillä kuin edelliselläkin kerralla. Kolmen ominaisuuden vaihtumisen kohdalla huomattiin, että on helpompaa ajatella, että vain yksi pysyy samana. Lopuksi muisteltiin aivojumpasta saatuja kokemuksia ja verrattiin omiin kouluaikaisiin kokemuksiin. ”Tämä on erilaista matematiikkaa kuin aikanaan koulussa.”  ”Erilainen näkökulma matematiikan oppimiseen!” ”Tämä on kivaa!” ”Jotain muutosta tuntuu tapahtuneen aivoissa, vaikka on vaikea sanoa, mitä.”

Loppupohdiskelua

Oli uskomaton kokemus, miten kahdeksankymppiset seniorit voivat kiinnostua ja jopa innostua matematiikasta! Osallistujilla oli hyvin erilaiset taustat. Osalla oli huonoja kokemuksia kouluajan matematiikan opiskelusta, mikä on heijastunut aina tähän päivään asti. ”Inhoan matikkaa! En ole tarvinnut sitä koulun jälkeen!” Useimpien kokemukset olivat neutraaleja: ”En muista mitään, en ole tarvinnut sitä koulun jälkeen!” Muutamilla on ns. matemaattinen tausta: matematiikan opiskelu oli helppoa koulussa ja he valitsivat matematiikan tai siihen liittyviä opintoja yliopistossa. Myös työelämässä he ovat tarvinneet paljon matematiikkaa.

Kaikkien työskentely kerhossa oli kuitenkin aktiivista taustasta riippumatta. Tunnelma oli mukava. Keskustelut työskentelyn lomassa ja sen jälkeen avasivat osallistujien kokemuksia ennen ja nyt. Taustat eivät vaikuttaneet tapaan tehdä tehtäviä. Kukaan ei ylpeillyt osaamisesta, vaan kaikki auttoivat ”vaivihkaa” toisiaan. Monet totesivat ääneen: ”Olen tyhmä! En osaa tehdä tällaista!” Yleensä tästä päästiin yli pienen kannustuksen ja kokeilun avulla: ”Minähän osaankin! Minä olen hyvä!” 

Ryhmissä keskusteltiin vilkkaasti, mutta muutama halusi pohtia ja tehdä rauhassa itsekseen ja sekin oli tietysti mahdollista. Myönteinen suhtautuminen ohjaaja Hanneleen oli jopa liikuttavaa: ”On ihanaa, kun ope ei huuda!” ”Täällä saa tehdä virheitä eikä kukaan hauku tyhmäksi!” ”Tänne on aina niin kiva tulla!” Saga-matikka antoi myös ohjaajalle enemmän kuin etukäteen oli kuviteltavissa: mielekästä sisältöä eläkeläisen arkeen!

Hannele haastatteli seitsemää kaikilla kokoontumiskerroilla mukana ollutta osallistujaa. Tällöin oli myös mahdollisuus keskustella heidän kirjoittamistaan muisteloista omalta kouluajalta. Kaikki olivat sitä mieltä, että tällaista matemaattista aivojumppaa pitäisi olla tarjolla myös muualla. Tämä toive toteutuu, sillä seniorikerhon kokemuksiin perustuva toimintaohjevihkonen on tulossa. Se tulee vapaasti saatavaksi ELLIn verkkokaupan sivuille nimellä Matemaattista aivojumppaa senioreille. Vihkonen sisältää tarkempien ohjeiden lisäksi osallistujille jaetut kirjalliset tehtävä- ja työskentelypohjat.

Kerhoa pidettiin harvakseen, vain yksi tunti joka toinen viikko, joten oli aikaa suunnitella sisältöjä. Alussa Hannele kertoo olleensa kovin epävarma siitä, miten osallistujat suhtautuisivat. Onko liian helppoa, liian lapsellista, liian vaikeaa? Kun oli tavattu muutaman kerran, hän sai heiltä sellaista palautetta, että alkoi luottaa omiin kokemuksiinsa. ”Olet niin innostunut matikasta, että se tarttuu meihinkin.” ”Nämä tehtävät ovat juuri sopivia meille. On hyvä, että aina kannustat meitä yrittämään, vaikka alku olisikin vierasta meille. Me luotamme sinuun, että osaat valita uudetkin sopivat tehtävät.”

”Monipuolinen kokemus matematiikan opettamisesta kaikilla luokilla 1–9 ja yksityisopettajana on opettanut ottamaan huomioon osallistujien tason ja kiinnostuksen. En siis joutunut tekemään sen kummempia muutoksia senioreiden kanssa”, sanoo Hannele. Onnistumista todistaa sekin, että kaikki haluavat jatkaa syksyllä, niin kuin ohjaaja itsekin. Uusia pelejä on jo tilattu entisten lisäksi. Tarkoituksena on muuttaa vähän työskentelyä. Nyt oli tehty ohjeiden mukaan samoja tehtäviä eri ryhmissä ja myös eriyttäen tarpeen mukaan. Syksyllä tehdään niin, että ryhmissä pelataan loogista ajattelua kehittäviä ja kymmenjärjestelmän ideaa avaavia pelejä. Mutta se onkin sitten aivan uusi tarina.