Hyperavaruutta esineellistämässä
Niin matematiikan kuin taiteenkin alalla on täysin luvallista tutkia sellaisia asioita, joita ei ole lainkaan olemassa luonnollisessa todellisuudessamme. Vaikka arkihavaintomme jäsentää ympäristömme geometrisen tilallisuuden ainoastaan kolmeksi toisiinsa nähden kohtisuoraksi suunnaksi – korkeudeksi, leveydeksi ja syvyydeksi, on kuitenkin käsitteellisesti mahdollista kuvitella uusi tilaulottuvuus suorassa kulmassa jo olemassa oleviin ulottuvuuksiin. Ajatusleikillä tällaisesta korkeampiulotteisesta tilasta on ollut syvällinen ja kauaskantoinen vaikutus filosofian, mystiikan, matematiikan, ja teoreettisen fysiikan lisäksi myös esimerkiksi kaunokirjallisuuteen ja kuvataiteeseen.
Eriulotteisten avaruuksien mahdollistamia geometrisia muotoja tarkastellessa erityistä huomiota ansaitsevat niin sanotut säännölliset rakenteet, joissa kaikki kärkipisteet, särmät ja tahkot ovat keskenään samanlaisia. Kaksiulotteisen tason tapauksessa on helppo huomata, että itse asiassa kaikki säännölliset monikulmiot toteuttavat tämän vaatimuksen. Kolmiulotteisessa tilassa tilanne on mielenkiintoisempi, sillä määritelmänmukaisia kappaleita on vain viisi: tetraedri, kuutio, oktaedri, dodekaedri ja ikosaedri. Nämä niin kutsutut Platonin kappaleet rakentuvat siis säännöllisistä monikulmioista, jotka liittyvät toisiinsa vinosti särmistään sulkeutuen lopulta itseensä käpertyen yhtyväksi pinnaksi.

Seuraten samanlaista päättelyä, jolla monitahokkaat rakentuvat kaksiulotteisista monikulmioista, voimme kuvitella kokoavamme neliulotteisia kappaleita liittämällä monitahokkaita toisiinsa tahkoistaan. Kun tämä liittäminen tehdään vinosti – mikä on mahdollista vain neliulotteisessa tilassa, saadaan tuloksena suljettuja, itseensä käpertyen yhtyviä rakenteita, joita voimme hyvällä syyllä pitää monitahokkaiden neliulotteisina vastineina. Jos vielä vaadimme, että rakenteen kärkipisteet, särmät, tahkot, ja solut ovat keskenään samanlaisia, rajoittuu mahdollisten muotojen määrä kuuteen.
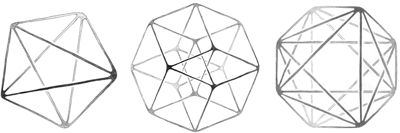
Koska tällaisten, vain matemaattisesti kuvailtujen hypermuotojen visuaalinen hahmottaminen tuntuu aluksi vaikealta, on hyödyllistä vertailla matalampien ja korkeampien tilaulottuvuuksien vuorovaikutusta niiden hierarkkisessa järjestyksessä. Ulottuvuuksien välisen vastaavuussuhteen kautta ajateltuna ne haasteet, joita me kohtaamme yrittäessämme kuvitella ja käsittää neliulotteisia kappaleita, ovat luonteeltaan samanlaisia kuin mitä yhtä lailla kuvitteellisen kaksiulotteisen maailman asukkailla olisi kolmiulotteisten muotojen ymmärtämisessä. Tästä seuraa myös, että aivan kuten kolmiulotteisia rakenteita voidaan esittää piirustuksien, maalauksien, valokuvien ja digitaalisten näyttöjen kaksiulotteisilla pinnoilla esimerkiksi poikkileikkauksina, aukilevityksinä ja projektioina, voidaan neliulotteisten kappaleiden kuvalliseen esittämiseen käyttää näiden tekniikoiden korkeampiulotteisia vastineita. Hypertilalliset rakenteet voidaan siis ’litistää’ meidän maailmaamme mahtuviksi – joskin vääristyneiksi, kolmiulotteisiksi kuvallisiksi esityksiksi.
Aalto-yliopiston Taiteen laitokselle tekemäni väitöstutkimuksen Hyperspatial Interlace – Grasping Four-dimensional Geometry Through Crafted Models päämääränä oli löytää uusia tapoja säännöllisten neliulotteisten kappaleiden kuvalliseen esittämiseen kolmiulotteisten, käsin kosketeltavien esineiden muodossa. Koska digitaalisin välinein tuotetut esitykset kuten 3D-tulosteet, virtuaalitodellisuudet ja vuorovaikutteiset ohjelmistot ovat yliedustettuina matemaattisen visualisoinnin alueella, halusin omassa työssäni mallintaa hyperkappaleita perinteisiä menetelmiä käyttäen. Tutkimusmenetelmänäni oli siis deskriptiiviseen geometriaan pohjautuva kokeellinen askartelu alkeellisia materiaaleja ja yksinkertaisia tekniikoita käyttäen. Neljännen tilaulottuvuuden kulttuuriset ilmentymät esimerkiksi okkultismin ja tieteiskirjallisuuden saroilla toimivat työn runollisena innoituksena. Tällaista hanketta, jossa taiteen alalta koulutuksensa saanut tutkija soveltaa taiteen menetelmiä jonkin oman työskentelynsä ulkopuolisen ilmiön tarkasteluun, kutsutaan taiteelliseksi tutkimukseksi.
Tutkimukseni tuloksena syntyi viisi esinekonseptia, joista kukin mallintaa säännöllisiä hyperkappaleita erilaisia kuvallisia esitystekniikoita käyttäen. Yksi tällainen esine on Kinochoron – messinkikehistä koostuva liikuteltava malli, joka esittää kuusitoistasolua ns. stereografisessa projektiossa. Toisiinsa punoutuvien kehien muodostama kytkösrakenne mahdollistaa projektion muuntelun neliulotteista kiertoliikettä vastaavalla tavalla.
Toinen kehittelemistäni esineistä – Crooked House II, kuvaa hyperkuution tylpättyä muotoa topologisena upotuksena. Puuvillaisena tilkkutyönä toteutetun mallin väriä voidaan vaihtaa niin ikään hyperrotaatiolla: pullauttelemalla rakenteen kahdeksaa ’huonetta’ piiloon ja esiin vuoron perään.
Suunnittelemani esineet osoittavat uusia poikkitieteellisiä yhteyksiä matematiikan ja kuvataiteen välillä, sekä auttavat kuvalliseen työskentelyyn liittyvien tilallisten ilmaisumuotojen rikastamista ja uudelleenymmärtämistä moniulotteisen geometrian kontekstissa. Tutkimukseni edistää myös osaltaan puhtaan matematiikan saavutettavuutta, sekä taiteellisen tutkimuksen metodologian kehitystä yhtenä ennakkotapauksena epätavallisen teoreettisen lähestymistavan käytöstä.
Erityinen merkitys työlläni on vanhempi yliopistonlehtori Kirsi Peltosen luotsaamalle Aalto Math&Arts ‑hankkeelle (matharts.aalto.fi), jonka poikkialaiseen opetustoimintaan esinekonseptini antavat uusia näkökulmia, sekä havainnollistamis- ja työskentelytapoja. Aalto Math&Arts -hankkeen tarkoitus on käynnistää uusi matematiikan ja taiteen sivuainekokonaisuus, kehittää edellytyksiä oppiaineiden väliselle yhteistyölle, sekä ankkuroida taiteellinen ajattelu ja kehollis-visuaaliset työtavat kiinteäksi osaksi matematiikan opettajankoulutusta. Elokuussa 2020 Aalto-yliopisto avaa ovensa myös matematiikan ja taiteen vuosittaiselle Bridges-konferenssille (bridgesmathart.org).
Kuluneena lukuvuonna tutkimustyöni on jatkunut osana LUMATIKKA-ohjelmaa (lumatikka.luma.fi), joka on täydennyskoulutusohjelma matematiikan parissa työskentelevälle opetushenkilöstölle. Ohjelman puitteissa olen suunnitellut ja toteuttanut työpajoja, joilla tutustutaan matemaattisten esineiden tarjoamiin monipuolisiin mahdollisuuksiin poikkitieteellisen oppimisen välineenä. Esineiden suunnittelu ja rakentaminen johdattelevat matematiikan tutkimiseen ja hyödyntämiseen eri aloilla. Tikkuasetelmien, geometristen rakennuspalikoiden ja modulaaristen paperimallien kautta olemme sivunneet projektiivista geometriaa, korkeampia tilaulottuvuuksia, rakenteita ja kinetiikkaa eri näkökulmista. Kirsi Peltonen on myös järjestänyt origamityöpajoja (Taide taittaa matematiikkaa”, Dimensio-lehti 3 ja 4, 2016), joiden aikana on käsitelty origamien historiaa, moderneja sovelluksia tekniikassa sekä avoimia tutkimuskysymyksiä, moduuliorigamien, origamitesselaatioiden, käyräviivaisten origamien ja geometristen rakenteiden kautta. Tarkoituksemme on houkutella myös kuvataiteen opettajia mukaan poikkialaiseen yhteistyöhön, sillä niin kuin taiteella matematiikalle, on myös matematiikan ilmiöillä ja lähestymistavoilla on paljon tarjottavaa taiteelliselle työskentelylle sen eri muodoissa.
Aloituskuva: Joel Filipe / Unsplash







