Matemaattisen ajattelun kielentäminen ymmärtävän oppimisen perustana

Artikkelin tarkoituksena on avata kielentämistä pedagogisena lähtökohtana matematiikan opetuksessa. Kielentämisen periaatteita avataan ja konkretisoidaan tehtäväesimerkkien avulla. Kielentäessään oppilas saa mahdollisuuden rakentaa matemaattista ajatteluaan puhekielen ja kirjoitetun kielen (luonnollinen kieli), piirroksin/kuvin, graafisin esityksin (kuviokieli) sekä matematiikan symbolikielellä. Parhaimmillaan matemaattisen ajattelun ilmaiseminen kielentämisen avulla tarkoittaa monipuolista matemaattisen ajattelun rakentamista sallivassa ja vapautuneessa oppimisen ilmapiirissä, jossa oppilaat oppivat toistensa ajattelusta. Käyttäessään kielentämistä opetuksessa pedagogisena lähtökohtana myös opettaja oppii kuuntelemaan oppilaiden ajatuksia sekä seuraamaan oppilaiden työskentelyä. Tällä tavalla opettaja saa arvokasta tietoa oppilaiden osaamisen tasosta ja voi suunnitella mahdollista ohjauksen ja tuen tarvetta.

Johdanto

”Miten ajattelit?” on kysymys, jonka haluaisimme kuulla matematiikan oppimisympäristöissä usein. Kun oppilaat kertovat, miten he ovat päässeet tehtävän ratkaisuun tai miten he ymmärtävät esimerkiksi kertolaskun käsitteen, he samalla prosessoivat ajatteluaan. Jakamalla ajatteluaan oppilaat oppivat toisiltaan ja opettajalla on mahdollisuus saada arvokasta tietoa oppilaiden ajattelusta. Monipuolisessa matematiikan oppimisympäristössä kuuluu oppilaiden ajatusprosessien selitykset, näkyy työskentely erilaisten kehollisten harjoitusten ja välineiden avulla sekä kirjoittaminen ja piirtäminen. Viimeisenä vaiheena tulee työskentely abstraktion tasolla matematiikan kielellä symbolisessa muodossa. Pedagogisena lähestymistapana opetuksessa kielentäminen antaa oppilaille tilaa tuoda esille ajatteluaan, oppia toisiltaan ja jäsentää omaa ajatteluaan sekä rikastaa matematiikan oppimisen tilanteita. Lähestymistapa vapauttaa oppimisen tilanteita ja antaa luvan erehtyä ja väitellä. Näin oppimisen ilmapiiristä tulee vapautunut ja salliva. Tossavainen ja Joutsenlahti (2018) tuovat esille, miten matematiikan opetuksen tehtävänä on auttaa oppilasta ymmärtämään matematiikkaa ja luomaan matematiikan sisällöistä tietorakenne, jota hän voi soveltaa ymmärtäen uusissa tilanteissa eikä vain muistinvaraisesti. Tässä nousee esille omakohtaisten ja monipuolisten kokemusten merkitys matematiikan oppimisen pohjana. Kun oppilas ilmaisee itseään puhuen tai kirjoittaen (luonnollinen kieli), piirtäen tai kuvilla (kuviokieli) symbolikielen rinnalla joustavasti liikkuen eri kielten välillä, hän ajattelee matematiikkaa ja rakentaa matemaattista ymmärrystään ja tietorakennetta. Tämän artikkelin tarkoituksena on kuvata kielentämisen merkitystä matemaattisen ymmärryksen rakentajana. 

Matemaattisen ajattelun kielentäminen

Matematiikan kielentämisessä painotetaan matemaattisen ajattelun kehittämistä, mikä on asetettu keskeiseksi tavoitteeksi kaikissa peruskoulun opetussuunnitelmien perusteissa viime vuosikymmeninä (Joutsenlahti, 2005; esim. OPS, 20142014). Matemaattisen ajattelun käsitteen määrittelystä ei ole olemassa yhtenäistä näkemystä. Tässä yhteydessä matemaattinen ajattelu voidaan ymmärtää oppilaan matemaattisen tiedon (käsitetiedon ja toimintaohjeiden) prosessointina, jota ohjaavat oppilaan tieto omista kognitiivisista taidoistaan ja niihin liittyvistä prosesseista (metakognitiiviset tiedot ja taidot) (Joutsenlahti, 2005, vrt. Pehkonen & Rossi, 2018; Stenberg, 1996). Kielentämisellä tarkoitetaan tässä artikkelissa matemaattisen ajattelun ilmaisemista pääasiassa kolmen semioottisen järjestelmän avulla: luonnollisella kielellä (puhe ja kirjoitus), kuviokielellä (piirrokset/kuvat/graafiset esitykset) ja matematiikan symbolikielellä (Joutsenlahti & Kulju, 2017; Joutsenlahti & Perkkilä, 2019). Tähän voidaan vielä lisätä erityisesti alakoulussa keskeinen taktiilinen toiminnan kieli (kehollinen kieli ja työskentely välineillä; ks. Kuvio 1) (Joutsenlahti & Rättyä, 20152015). 

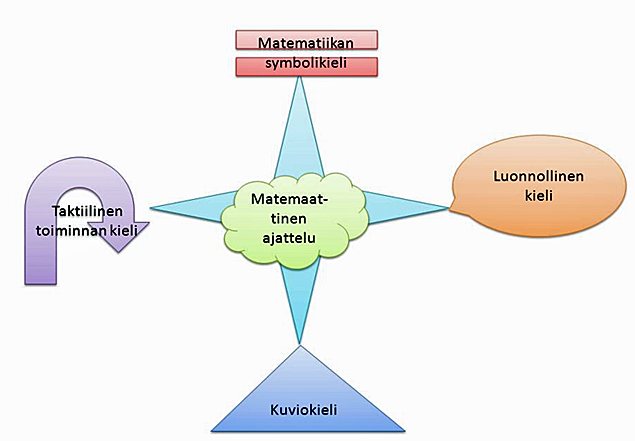
Taktiilisella toiminnan kielellä oppilas voi havainnollistaa esimerkiksi lukualueella 0–20 kymmenylitystä ja -alitusta kananmunakennojen ja mulltilink-kuutioiden avulla. Kun edellä mainittuun esimerkkiin liitetään omin sanoin luonnollisella kielellä kerrotut tarinat ja piirrokset, niin saadaan vielä monipuolisempaa tietoa oppilaan matemaattisesta ajattelusta. Lopuksi voidaan sopia yhteisesti matematiikan symbolikielen mukaisista merkinnöistä. Yleensä matematiikan symbolikielen mukaiset määritelmät ja lauseet voidaan esittää myös luonnollisella kielellä. Useiden kielten monipuolista käyttöä samassa tilanteessa voidaan kuvata esitettyjen merkitysten koodinvaihtona Kuviossa 1 esitettyjen kielten välillä. Tämä auttaa oppilaita ymmärtämään opittavien käsitteiden sisältöä tai kuvaamaan tehtävien ratkaisuprosesseja monipuolisesti. (vrt. Perkkilä & Joutsenlahti, 2019; Joutsenlahti & Tossavainen, 2018; Joutsenlahti & Kulju 2017.)

Lev Vygotski tutki jo 1930-luvulla kielen merkitystä ajattelun rakentumisen kannalta sekä kielen ja ajattelun välistä suhdetta. Vygotski näkee ajatuksen olevan perustana ajattelijan tavoitteelle, joka toteutuu sanojen ilmaisuina. Sanojen merkitys avautuu niihin liittyvien asioiden tai kohteiden yhteyksien tai suhteiden järjestelmissä. Ajatuksen ja ulkoisen puheen yhdistää niiden välillä oleva sisäinen puhe, puhe itselle. Sisäinen puhe on muodoltaan tiivistettyä puhetta, jonka osien ympärille ulkoisen puheen lauseet rakentuvat. (Vygotski, 1982.; Joutsenlahti & Rättyä 2015). Esimerkiksi silloin, kun oppilas selittää tehtävän ratkaisua omin sanoin luonnollisella kielellä toisille oppilaille, rakentaa tämä selitys (ulkoinen puhe) toisten oppilaiden ajattelua. Toisaalta selittävän oppilaan on jäsennettävä ulkoisella puheella ilmaistava ajatus ensin itselleen, jolloin hänen ulkoinen puheensa toimii myös hänen ajattelunsa jäsentäjänä ja kehittäjänä. Voidaankin sanoa, että ulkoinen puhe rakentaa kuulijoiden ymmärrystä, ajattelua, heidän sisäisen puheensa kautta. Oppilaan ulkoinen puhe hänen ajattelunsa ilmentymänä on myös opettajan arvioinnin kohde, jota opettaja voi käyttää opetuksen suunnitteluun ja arviointiin tavoitteiden saavuttamisesta.  (vrt. Joutsenlahti & Rättyä 2015.) Näin luonnollinen kieli tukee ajattelun kehittymistä ja ymmärrystä. Kun matematiikan luonnollinen kieli liitetään kielentämisen muihin osa-alueisiin (ks. Kuvio 1), ja mahdollistetaan koodinvaihto eri osa-alueiden välillä, niin voidaan kehittää oppijan ajattelua monipuolisesti ja samalla myös prosessissa syntyneet uudet ajatukset vahvistavat ja syventävät ymmärrystä matemaattisista käsitteistä ja ilmiöistä monipuolisesti. Lisäksi vertaisryhmä kehittää vastaavasti omaa ajatteluaan ja opettajalle mahdollistuu jatkuva arviointi.

Esiopetus

”Lapsia innostetaan pohtimaan ja kuvailemaan matemaattisia havaintojaan erilaisissa arjen tilanteissa opettajan mallintamisen ja kielellistämisen avulla. Havaintoja harjoitellaan esittämään itse ja kuvien sekä erilaisten välineiden avulla.”(EOPS 2014, 36) (Käytämme Esiopetuksen opetussuunnitelman perusteista lyhennettä EOPS)

Esiopetuksen opetuksen opetussuunnitelman perusteet (2014) painottaa oppilaan omaa tekemistä ja toimimista. Tähän voidaan lukea niin puhe ja kertominen kuin mallintaminen välineillä sekä kertominen piirrosten ja kuvien avulla. Keholliset leikit, esimerkiksi taputukset, tömistykset, hyppelyt ja pyörimiset, ovat olennainen osa esiopetuksen matemaattisia oppimisympäristöjä. Lukujen ymmärtämistä voidaan tukea taputusleikillä opettajan ohjauksessa ”Taputa yhtä monta kertaa kuin minä taputan”. Kehollisuudesta voidaan siirtyä kielentämisen seuraavaan vaiheeseen, jossa etsitään ympäristöstä yhtä monta esinettä kuin taputuksia oli. Seuraavaksi sovitaan esineryhmää kuvaava numeromerkki ja vietä toistetaan se näin: Minulla on viisi kuutiota tai pikkuautoa tai nallea jne. Oppilaat voivat myös piirtää löytämänsä esineet ja kirjoittaa niiden viereen lukumäärää vastaavan numeromerkin. 

Luonnollisen kielen merkitys esikoululaisen matematiikan oppimisessa on merkittävä. Kertoessaan omin sanoin omalla äidinkielellään, miten hän ymmärtää oppimisen kohteena olevan asian, opettaja saa arvokasta tietoa oppilaan matemaattisesta ajattelusta ja sanavaraston laajuudesta. Monipuolisella sanavarastolla on merkitystä myös matematiikan oppimisessa. Seuraavassa kuviossa 2 on tehtävä-esimerkki (Niittumäki, 2010) siitä, miten esikoululaisten kanssa voi harjoitella luonnollisella kielellä pienten matematiikkatarinoiden kertomista.

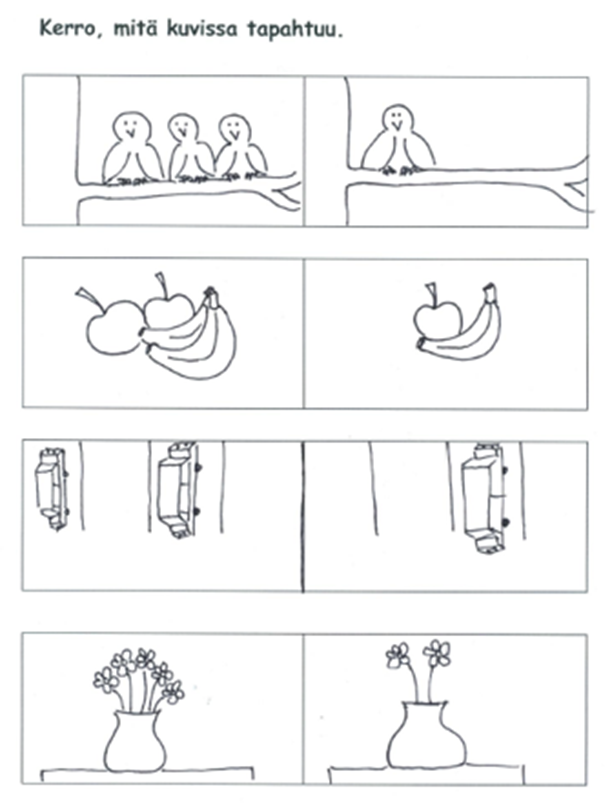
Kuvion 2 tehtävät ovat ”ennen–jälkeen” -tehtäviä, joiden avulla voidaan esikoululaisia harjoittaa kertomaan tarinoita peräkkäisistä tapahtumista. Tällaisia tehtäviä voidaan tehdä myös kuvasarjojen avulla, jotka tehty erillisille korteille. Tällöin oppilasta pyydetään ensin järjestämään kortit tapahtumajärjestykseen ja sitten kertomaan tarina. Tällainen työskentely vaatii opettajan ohjausta lapsen lähikehityksen (Vygotski, 1982) vyöhykkeellä. Esittämällä esikoululaisen lähikehityksen vyöhykkeellä oikea-aikaisia kysymyksiä, opettaja saa oppilaan kertomaan tarinaa  ja jäsentämään kuvien sisältöä sekä tuomaan esille matemaattista ajatteluaan. Näin omin sanoin kielentämällä oppilaat saavat hyviä kokemuksia oman ajattelunsa kielentämisestä. Kuvion 2 kaltaisten harjoitusten pohjalta oppilaat voivat myös piirtää omia matemaattisia tarinoita sekä rakentaa niitä toimintamateriaaleilla tai leluilla. Näin esikoululaiset harjoittelevat tuomaan esille matemaattista ajatteluaan luonnollisella kielellä kuvien sekä erilaisten välineiden/lelujen ja omien piirrosten avulla (vrt. EOPS, 2014).

Alkuopetus

” Opetus kehittää oppilaan kykyä ilmaista matemaattista ajatteluaan konkreettisin välinein, suullisesti, kirjallisesti ja piirtäen sekä tulkiten kuvia.” (lk. 1–2, POPS 2014)

Edellä esitetty opetussuunnitelman perusteiden tavoite voidaan toteuttaa esimerkiksi tehtävärakenteella, joka perustuu kolmen kielen (ks. Kuvio 1) käyttämiseen ohjatusti samassa tehtävässä. Kuvataan tilanne yhdellä kielellä ja tehtävänä on säilyttää matemaattiset merkitykset muiden kielten kuvauksissa. Kuviossa 3 on ensimmäinen sarake varattu luonnollisella kielellä annettuun tehtävänantoon (sanallinen tehtävä), toinen sarake esimerkiksi kymmenen munan kenno(t) (toimintamateriaali) kuviokielisenä ja kolmantena matemaattiset lausekkeet matematiikan symbolikielellä.  

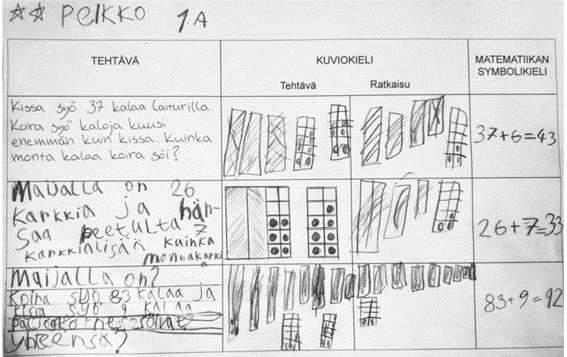
Kuvion 3 tehtävämalliin on tuotu kielentämisen mallin neljäskin kieli (taktiilinen toiminnan kieli) mukaan siten, että kuviokielen käyttö rajoitetaan tässä vain toimintamateriaalin käytön kuvaukseen. Munakennot voivat olla konkreettisina materiaaleina ohessa käytössä, mutta ratkaisuprosessi niiden kautta kirjataan kaksivaiheisena sarakkeisiin ”Tehtävä” (lähtötilanne) ja ”Ratkaisu” (lopputilanne). Tässä (Kuvio 3) kymmenen ykkösen täyteen tuleminen kennossa ja sen jälkeen suljettu kenno yhtenä kymmenenä on piirretty värjäämällä vastaava suorakulmio mustaksi. Jos lähtötilanne on annettu jollakin muulla kielellä kuin luonnollisella kielellä, niin ratkaisija voi luoda tehtävänannon kontekstin vapaasti mielekkäällä tavalla annetut lukumäärät huomioiden. Oppilaan selittäessä ratkaisuaan hän kielentää suullisesti (luonnollisella kielellä) miten hän on koodannut matemaattiset merkitykset kieleltä toiselle ja miten ratkaisuprosessin vaiheet etenevät alkutilasta lopputilaan. Tässä mallissa kuviokielen osuus voidaan myös ottaa käyttöön ilman kuvioihin liittyviä rajoituksia eli oppilas saa piirtää luonnollisella kielellä kuvatut kohteet piirtämällä ne. Tällöin kuviokieleen riittää yksi sarake. Tehtävämalli voidaan toteuttaa esimerkiksi lukiossa tai yliopistossa siten, että luonnollisen kielen osuus sisältää matemaattisten käsitteiden ja niiden ehtojen kuvaukset. Kuvion 3 tehtävämalli voisi parhaimmillaan toteuttaa alussa kuvatun tavoitteen, jossa oppilas kuvaa ”matemaattista ajatteluaan konkreettisin välinein, suullisesti, kirjallisesti ja piirtäen sekä tulkiten kuvia” (POPS 2014).   

Perusopetuksen luokat 3–9

”Opetus kehittää oppilaan taitoja esittää matemaattista ajatteluaan ja ratkaisujaan eri tavoilla ja välineillä.”

”Täsmällinen ilmaisu on oppilaalle hyödyllinen matematiikassa opetettava taito. Oppilasta rohkaistaan esittämään ratkaisujaan ja keskustelemaan niistä.” (lk. 3–6 ja lk. 7–9, POPS 2014)

Tehtävien ratkaisuina voi olla laskutoimitusten lisäksi käsitteiden ja niiden välisten suhteiden löytämistä kootusti. Kuvion 4 moniosaisessa tehtävässä oppilaat löytävät yhdessä kaksi erilaista jakolaskua ja ymmärtävät niiden eron muodostamalla kaksi erilaista kysymystä, joista toiseen vastauksena tulee viisi euroa (ositusjako) ja toiseen kolme ryhmää tms. (sisältöjako).  Mainittujen käsitteiden ero saatetaan ymmärtää parhaiten omien kysymysten rakentamisprosessien kautta. Siihen ei riittäne pelkkä muistinvarainen tieto, vaan oman aktiivisen ajattelun kautta rakennetaan tilanteeseen sopivat kysymykset. Tämä johtaa parhaimmillaan ymmärrykseen näiden vaikeiden käsitteiden väliseen suhteeseen.

Mainittu tehtävä liittää myös jakolaskun ja kertolaskun käsitteet toisiinsa. Kuvaparin tutkiminen päinvastaisessa järjestyksessä tuo näkyviin näiden laskutoimitusten käänteisyyden. Hyvä kysymys lienee myös, että jos olemme löytäneet kaksi erilaista jakolaskua, niin mitkä ovat käänteisenä laskutoimituksina kertolaskut? Ovatko ne erilaisia? Tämä tehtävä tuo parhaimmillaan luvun alussa esitetyn tavoitteen ”Oppilasta rohkaistaan esittämään ratkaisujaan ja keskustelemaan niistä” (POPS, 2014), sillä oppilaiden suullinen argumentointi ja erilaisten ratkaisujen reflektointi omin sanoin tuottaa parhaimmillaan oppilaille ymmärrettävien matemaattisten käsiteverkkojen kehittymistä.  

Tehtävät, joissa oppilaat selittävät ja perustelevat luonnollisella kielellä matemaattisia ratkaisuprosesseja, antavat toisen asteen matematiikan opiskelulle käsitteellisen ymmärtämisen ja mukautuvan päättelyn perustaa. 

Lopuksi

Edellä esitetyillä esimerkeillä kielentämisestä haluamme näyttää, että matemaattisen ajattelun monipuolinen ilmaisu Kuvion 1 kielten kautta auttaa ymmärtävään oppimiseen matemaattisen sisällön kognitiivisesta vaativuudesta ja ajattelijan iästä riippumatta. Oppilaan ratkaisun kuvaaminen hänen omin sanoin ja kielikuvin osoittaa kuulijalle tai lukijalle, miten ratkaisu ja siihen liittyvät reunaehdot on ymmärretty. Useat kokevat tämän mielekkääksi työtavaksi matematiikan opiskelussa, sillä silloin he voivat itse aktiivisesti rakentaa merkityksiä opiskeltaville matematiikan käsitteille ja proseduureille. Tältä osin voidaan ajatella, matematiikan opetus hyödyntäessään kielentämistä yksilöllistää oppimispolkuja. Toisaalta kielten avulla ollaan vuorovaikutuksesta luokkatilanteissa vertaisryhmän kanssa, jolloin oppimisesta tullee ryhmän yhteinen tiedon muodostamisprosessi. Ja kaikkea tätä voi opettaja ohjata ja arvioida.

Tämän artikkelin kielentämisen tehtävien ja Kuvion 1 perusteella on nähtävissä, miten kielentäminen antaa oppilaille tilaa rakentaa matemaattista ajatteluaan omista lähtökohdistaan. Kielentämisessä toteutuu parhaimmillaan ajatus siitä, että oppilaat voivat sekä oppia toisten vertaisoppijoiden ajattelusta että kyseenalaistaa toinen toistensa ajattelua. Myös opettaja oppii ja rakentaa ajatteluaan keskittyessään kuuntelemaan ja seuraamaan oppilaiden matemaattisen ajattelun ilmauksia. Samalla hän saa tietoa siitä, mitä oppilaat osaavat ja mihin he tarvitsevat ohjausta ja tukea. Oppilas voi valita lähtökohdaksi tehtävän ratkaisussa sen kielentämisen osa-alueen, joka on lähimpänä hänen kokemusmaailmaansa sekä matemaattista tietorakennettaan. Valitsemastaan lähtökohdasta hän voi koodinvaihdon avulla tarkastella tehtävän ratkaisua muiden kielentämisen osa-alueiden avulla. Näin oppilas rakentaa ja luo laaja-alaisempaa sekä monipuolisempaa pohjaa matemaattiselle ymmärrykselleen. 

Valmiit mallit ja ulkoa opettelu eivät rakenna ymmärrystä. Monipuolinen tiedonrakentelu oman tekemisen kautta, oivallukset, vapaus tuoda esille ajatteluaan monipuolisesti, onnistumisen elämykset sekä erityisesti oppimisen omistajuus antavat oppilaille vapauden oppia omista lähtökohdistaan ja olla osa oppivaa yhteisöä. 

Kuvion 1 neljän kielen malli antaa mahdollisuuden suunnitella matematiikan opetusjärjestelyjä erityisille oppilasryhmille, kuten esimerkiksi maahanmuuttajille ja näkövammaisille. Mallissa voidaan ajatella oppilaan heikoin kieli korvattavaksi kolmella muulla tai niiden kombinaatioilla. Maahanmuuttajaoppilaan heikkoa Suomen kielen taitoa voidaan kompensoida kuviokielellä ja taktiilisella toiminnan kielellä rakennettaessa merkityksiä uusille matemaattisille ilmiöille. Näkövammaiselle oppilaalle voidaan taktiilisen toiminnankielen (toimintamateriaaleilla) ja puhutulla luonnollisella kielellä luoda ymmärrys esimerkiksi lukumääristä ja niihin liittyvistä laskutoimituksista. Me kukin opimme parhaiten ajasta ja paikasta riippuen jollakin kielistä tai niiden kombinaatioista, mutta ymmärryksen kasvu voi tapahtua monella eri tavalla. Siksi näitä mallin kieliä pitää opetuksessa varioida ja kannustaa oppilaitakin tekemään niin avatessaan ajatteluaan.

Lähteet

EOPS. (2014). Esiopetuksen opetussuunnitelman perusteet 2014. Helsinki: Opetushallitus. Saatavilla https://www.oph.fi/sites/default/files/documents/esiopetuksen_opetussuunnitelman_perusteet_2014.pdf

Joutsenlahti, J. (2005). Lukiolaisen tehtäväorientoituneen matemaattisen ajattelun piirteitä. Tampereen yliopisto. Acta Universitatis Tamperensis 1061.

Joutsenlahti, J. & Kulju, P. (2017). Multimodal languaging as a pedagogical model – a case study of the concept of division in school mathematics. Education Sciences, 7(1), 9. Saatavilla Joutsenlahti, J. & Perkkilä, P. (2019). Sustainability development in mathematics education – a case study of what kind of meanings do prospective class teachers find for the mathematical symbol “2/3”? Sustainability, 11, 457. Saatavilla https://doi.org/10.3390/su11020457

Joutsenlahti, J. & Rättyä, K. (2015). Kielentämisen käsite ainedidaktisissa tutkimuksissa. Teoksessa M. Kauppinen, M. Rautiainen & M. Tarnanen (toim.), Rajaton tulevaisuus. Kohti kokonaisvaltaista oppimista. Ainedidaktiikan symposium Jyväskylässä 13.–14.2.2014. Suomen ainedidaktisen tutkimusseuran julkaisuja Ainedidaktisia tutkimuksia 8, 45–62.

Joutsenlahti, J. & Tossavainen, T. (2018). Matemaattisen ajattelun kielentäminen ja siihen ohjaaminen koulussa. Teoksessa J. Joutsenlahti, H. Silfverberg & R. Räsänen (toim.), Matematiikan opetus ja oppiminen. Jyväskylä: Niilo Mäki Instituutti, 410–430.

Lier, J. (2019). Alkuopetukseen erikoistujien kurssin harjoitustyö. Kasvatustieteiden ja kulttuurin tiedekunta, Tampereen yliopisto. Julkaisematon.

Niittumäki, S. (2010). Matematiikan kielentäminen varhaiskasvatuksessa. Kandidaatin tutkielma. Kasvatustieteiden tieteiden tiedekunta. Tampereen yliopisto. Julkaisematon.

Pehkonen, E. & Rossi, M. (2018). Hyvää matematiikan opetusta etsimässä. Helsinki: MFKA.

POPS (2014). Perusopetuksen opetussuunnitelman perusteet 2014. Helsinki: Opetushallitus.

Stenberg, R. (1996). What is mathematical thinking? Teoksessa R. Stenberg & T. Ben-Zeev (toim.), The nature of mathematical thinking. Mahwah, NJ: Lawrence Erlbaum.

Vygotski, L. (1982). Ajattelu ja kieli. Espoo: Weilin & Göös.