Benjihyppy – hypyistä hurjin?
Voidaanko perustellusti väittää, että benjihyppy on hurjempi kuin laskuvarjohyppy? Tähän kysymykseen vastataan fysiikan tiedon avulla. Kysymystä tarkastelemalla voidaan syventää lukiofysiikan mekaniikan sisältöjä esimerkiksi työkurssilla.
Nuori hurjapää miettii, hyppäisikö benji- vai laskuvarjohypyn. Molemmissa hypyissä lähdetään korkealta ja tullaan alas painovoiman vaikutuksessa, kunnes liikettä vastustavat voimat rauhoittavat menoa. Kauhua, kuoleman pelkoa, adrenaliinia ja hetkessä elämistä. Sitä nämä extreme-lajit tarjoavat kokeilijoilleen.
Laskuvarjohypyssä hyppääjä on etävuorovaikutuksessa maahan ja kosketusvuorovaikutuksessa ilmaan. Benjihypyssä hyppääjä on näiden lisäksi kiinnitetty benjiköyteen ja täten hän on kosketusvuorovaikutuksessa siihen. Voiko hyppääjästä roikkuva köysi tehdä hypystä hurjemman?
Benjihypyssä vapaan pudotuksen päätteeksi köysi ampaisee hyppääjän uudelleen ylöspäin ja lähettää hyppääjän ikään kuin ”uudelle kierrokselle”, joka tosin jää väistämättä ensimmäistä pudotusta maltillisemmaksi. Nyt jos tätä ”uusintahyppyä” ei huomioida vaan tarkastellaan pelkästään hyppääjän ensimmäistä putoamisliikettä, voiko benjihyppääjän putoamisliike olla laskuvarjohyppääjää hurjempi?
Vastaus riippuu siitä, miten ”hurjuus” määritellään. Jos hurjuus mitataan lentoaikana, silloin laskuvarjohyppy on tyypillisesti benjihyppyä pidempi. Toisaalta tällöin myös useiden tuntien lentomatka, esimerkiksi Helsingistä -Vancouveriin olisi laskuvarjohyppyä hurjempi, mutta harvoin lentoyhtiöiden matkassa kokee kauhua tai kuolemanpelkoa extreme-urheilun tavoin.
Ehkäpä lentoajan sijaan hurjuus olisi syytä rinnastaa hyppääjän kokemaan kiihtyvyyteen, sillä muun muassa sotilaslentäjien toimintakykyä mitataan kiihtyvyyden avulla ns. G-sietokykynä (Tuokko, 2019). Voiko benjihyppääjällä olla suurempi putoamiskiihtyvyys kuin esimerkiksi vapaasti tippuvalla esimerkiksi laskuvarjohyppääjällä?
Kysymystä voi lähestyä monella eri tavoin, esimerkiksi katsomalla mitä lukio-oppikirjat sanovat asiasta. ”Kappaleilla, joihin kohdistuva ilmanvastus on pieni, on putoamisliikkeessä massasta riippumatta sama kiihtyvyys, ja kiihtyvyyttä kutsutaan putoamiskiihtyvyydeksi” (Andersin; Frondelius; Latva-Teikari & Lehto, 2021, s. 32).
”Galilein putoamislain mukaan kaikki kappaleet putoavat painovoiman vaikutuksesta samalla kiihtyvyydellä, jos ei ole mitään vastustavia voimia.” (Hämmeri; Jokinen; Ketolainen; Sallinen & Sloan, 2010, s. 22).
”Kappaleilla, joiden ilmanvastus on pieni, on massasta riippumatta sama kiihtyvyys, joka on likimain yhtä suuri kuin gravitaation aiheuttama putoamiskiihtyvyys g.” (Lehto; Havukainen; Maalampi & Leskinen, 2009, s. 51)
Oppikirjojen perusteella vaikuttaa siltä, että benjihyppääjällä on yhtä suuri putoamiskiihtyvyys kuin laskuvarjohyppääjällä, mikäli ilmanvastuksen suuruus ei merkittävästi poikkea hyppääjien välillä.
Teoriatiedon lisäksi hyppääjien liikettä voidaan tarkastella kokeellisesti, esimerkiksi alla kuvatun koejärjestelyn avulla.
Koejärjestely
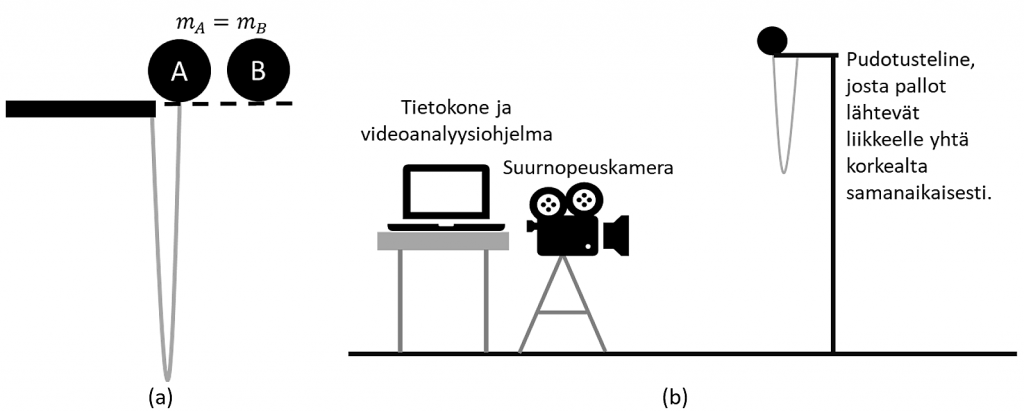
Tilanteen yksinkertaistamiseksi tarkastellaan benji- ja laskuvarjohyppääjiä, jotka ovat muodoltaan, kooltaan ja massaltaan identtiset. Mallinnetaan hyppääjiä tennispalloilla, joista toinen pallo kytketään benjiköyttä mallintavaan naruun. Naruksi valitaan metalliketju, joka tuo korostetusti esille benjiköyden massan vaikutuksen hyppääjän putoamiskiihtyvyyteen. Ketju kiinnitettään pallojen lähtöalustaan ja pallojen liikettä kuvataan suurnopeuskameralla Kuvien 1a ja 1b mukaisesti. Kameran kuvausnopeudeksi valitaan 240 fps, jolloin noin kahden metrin putoamismatkalta saadaan tarkasteltua pallojen paikkaa noin 150 kertaa 0,6 sekunnin putoamisliikkeen ajalta.
Tulokset
Kuvassa 2 on esitetty pallojen liike ennen putoamisliikkeen puoliväliä. Kuvasta 2 nähdään, että ketjuun kytketty pallo on hieman edellä vapaasti tippuvaa palloa, vaikka pallot ovat lähteneet liikkeelle samanaikaisesti yhtä korkealta.

Ero pallojen putoamismatkassa näyttää kasvavan putoamisen myötä, kuten on nähtävissä kuvissa 3a-c.

Mitä lyhyemmässä ajassa pallo liikkuu putoamismatkan, sitä suuremman nopeuden muutoksen se kokee putoamisliikkeen aikana. Mitä suuremman nopeuden muutoksen pallo kokee (saman tai lyhyemmän aikavälin aikana), sitä suurempi kiihtyvyys sillä on. Toisin sanoen pallojen putoamisliikkeen perusteella vaikuttaa siltä, että ketjuun kytketyllä pallolla on suurempi kiihtyvyyden suuruus kuin vapaasti putoavalla pallolla. Tämän päätelmän vahvistaa pallon liikkeestä tehty videoanalyysin tulos (ks. kuva 4), jonka mukaan pallo keskimääräiseksi kiihtyvyydeksi saadaan $13,3 \mathrm{m/s}^{2}$.
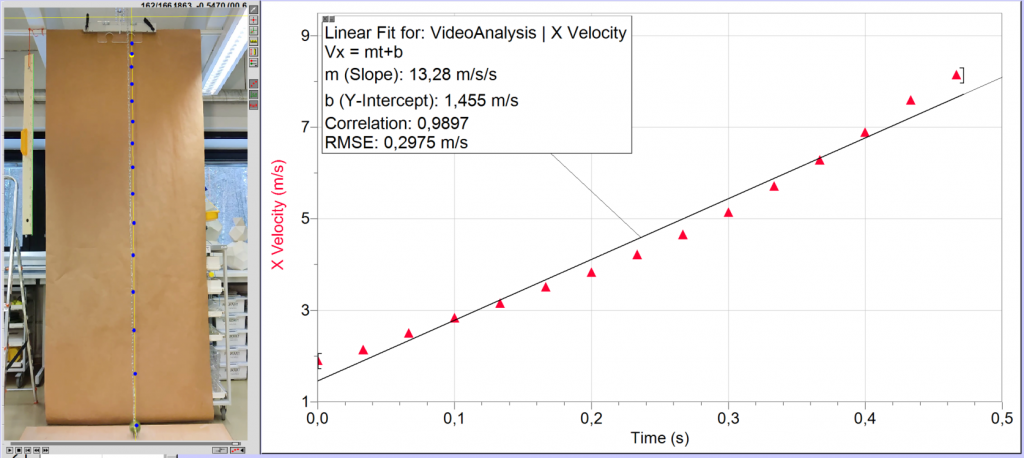
Saatu kiihtyvyys on siis suurempi kuin vapaasti putoavan kappaleen putoamiskiihtyvyyden vakioarvo $g = 9,81 \mathrm{m/s}^{2}$.
Tarkastellaan seuraavaksi yksinkertaista teoreettista mallia, jonka avulla voidaan osin selittää, miksi ketjuun kytketyn pallon putoamiskiihtyvyys on vapaasti putoavaa palloa suurempi.
Massakeskipistemalli
Ketjuun kytketyn pallon pudotessa, putoava systeemi koostuu pallosta ja palloon kiinnitetystä ketjusta, kuten esitetty Kuvassa 5a. Putoavan systeemin massakeskipiste (MKP) sijaitsee jossain pallon ja ketjun puolivälin välisellä tasolla (Ks. Kuva 5b). Merkitään $s_{MKP}$ pallon keskipisteen etäisyyttä putoavan systeemin massakeskipisteen korkeudesta. Massakeskipisteperiaatteen mukaan systeemin massakeskipiste liikkuu samalla tavoin kuin systeemiä vastaava pistemäinen kappale. Koska putoava systeemi on kokonaisuutena vapaassa putoamisliikkeessä, sen massakeskipisteen kiihtyvyys $a_{MKP}=g=9,81 \mathrm{m/s}^{2}$.
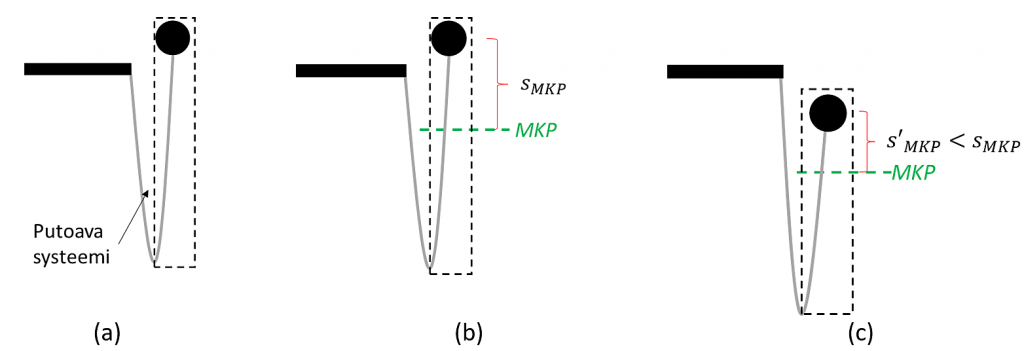
Pallon pudotessa alaspäin osa pallon mukana putoavasta ketjusta siirtyy lepoon taitoksen vasemmalle puolelle. Tällöin putoavan systeemin massa pienenee ja sen massakeskipiste siirtyy lähemmäksi palloa (ks. Kuva 5c). Toisin sanoen pallo saavuttaa putoavan systeemin massakeskipistettä. Jotta tämä on mahdollista, pallolla täytyy olla suurempi putoamiskiihtyvyys kuin putoavan systeemin massakeskipisteellä, $a_{MKP}=g = 9,81 \mathrm{m/s}^{2}$.
Tällaisella yksinkertaisella massakeskipistemallilla voidaan päätellä, miksi ketjuun kiinnitetyllä pallolla on suurempi putoamiskiihtyvyys kuin vapaasti tippuvalla pallolla.
Pohdinta
Yllä olevan analyysin pohjalta voidaan perustellusti esittää, että benjihypyn aikana hyppääjällä on teoriassa mahdollisuus kokea suurempi putoamiskiihtyvyys kuin vapaassa putoamisliikkeessä olevalla laskuvarjohyppääjällä. Tämä tulos voi olla yllättävä ja vaikuttaa ristiriitaiselta lukio-oppikirjojen sisältöjen kanssa. Lukio-oppikirjoissa painotetaan, että putoamiskiihtyvyys on massasta riippumaton vakio, kun ilmanvastus jätetään huomiotta (Andersin; Frondelius; Latva-Teikari & Lehto, 2021; Hämmeri; Jokinen; Ketolainen; Sallinen & Sloan, 2010; Lehto; Havukainen; Maalampi & Leskinen, 2009). Lukio-oppikirjoissa oletetaan, että putoavat kappaleet eivät menetä massaansa putoamisliikkeen aikana, mikä on usein perusteltu, vaikkakin harvoin esiin tuotu olettamus kappaleiden putoamisliikkeen tarkastelussa. Benjihypyn tapauksessa tämä olettamus ei ole voimassa, sillä hypyn aikana osa benjiköydestä siirtyy lepoon, jolloin putoavan systeemin massa pienenee.
Benjihyppääjän liike on innoittanut useita fysiikan opettajia ja tutkijoita tarkastelemaan ilmiötä opettamisen näkökulmasta. Esimerkiksi Kagan & Kott (1996) ovat johtaneet matemaattisen mallin benjihyppääjää mallintavan ketjuun kytketyn kappaleen putoamiskiihtyvyydelle mekaanisen energian säilymisen perusteella ja esittäneet koejärjestelyn, joka mahdollistaa matemaattisen mallin pätevyyden arvioinnin kokeellisesti. Mungan (2016) on tuonut esille energiatarkastelun ongelmallisuuden ja ehdottanut vastineeksi voimiin perustuvaa, ns. newtonilaista analyysiä (Mungan, 2018). Biezeveld (2003) on kehittänyt lukio-opetusta varten numeerisen laskentamenetelmän benjihyppääjän liikkeen kuvaamiseksi ajan suhteen. Menetelmällä hyppääjän liikettä voi tarkastella ajan suhteen ilman erikoisfunktioiden käsittelyä. Heck, Uylings ja Kedzierska (2010) ovat tuoneet esille lukiolaisten benjihyppyä käsittelevän projektin, joka herätti kansallista huomiota Hollannin fyysikkoyhteisössä. Osa yhteisön jäsenistä piti lukiolaisten saamia tuloksia benjihyppääjän kiihtyvyydestä ($>9,81\mathrm{m/s}^{2}$) mahdottomina, ennen kuin asiaan perehtynyt fyysikko vahvisti tulokset oikeiksi. Itä-Suomen yliopiston LUMA-keskuksella on kehitetty benjihyppääjän putoamisliikettä käsittelevä kokeellinen työ, jonka on havaittu tehokkaasti tukevan massakeskipistemallin oppimista (Kesonen; Leinonen & Asikainen, 2019). Nykyisin tämä kokeellinen työ on muutettu verkon yli tehtäväksi virtuaalityöksi, jonka sisältyy Itä-Suomen yliopiston Fysiikan perustyöt – virtuaaliset laboratoriotyöt -opintojaksoon. Halutessaan lukiolaiset voivat suorittaa opintojakson ja sen benjihyppääjän putoamisliikettä käsittelevän työ jatkuvan oppimisen väylää myöten Opintopolku.fi-sivuston kautta. Opettajilta saadun palautteen perusteella työ soveltuu esimerkiksi fysiikan työkurssille.
Lähteet
Andersin, J.; Frondelius, P.; Latva-Teikari, J. & Lehto, H. (2021). Fysiikka Fy4 Voima ja liike. Helsinki: Sanoma Pro Oy.
Biezeweld, H. (2003). The Bungee Jumper: A Comparison of Predicted and Measured Values. The Physics Teacher, 41, 238-241.
Heck, A.; Uylings, P. & Kedzieska, E. (2010). Understanding the physics of bungee jumping. Physics Education, 45, 63-72.
Hämmeri, K.; Jokinen, R.; Ketolainen, P.; Sallinen, M. & Sloan, M. (2010). Empiria 4 Liikkeen lait. Keuruu: Otava.
Kagan, D. & Kott, A. (1996). The Greater-Than-g Acceleration of a Bungee Jumper. The Physics Teacher, 34, 368-373.
Kesonen, M. H.; Leinonen, R. & Asikainen, M. (2019). Applying a simple model aiding in understanding the acceleration of a bungee jumper. Phyiscs Education, 54, 1-7.
Lehto, H.; Havukainen, R.; Maalampi, J. & Leskinen, J. (2009). Fysiikka 1 Fysiikka luonnontieteenä. Jyväskylä: Kustannusosakeyhtiö Tammi.
Mungan, C. (2016). The challenge of explaining why. The Physics Teacher, 54, 388-389.
Mungan, C. (2018). Newtonian Analysis of a Folded Chain Drop. The Physics Teacher, 56, 298-301.
Tuokko, V. (2019). Sotilaslentäjän toimintakyky. Kirjassa Puolustustutkimuksen vuosikirja 2019. https://puolustusvoimat.fi/-/puolustustutkimuksen-vuosikirja-2019-puolustustutkimus-100-vuotta.
LUMAn arkijuhla -juttusarja
Tässä juttusarjassa käsitellään Itä-Suomen yliopiston LUMA-keskuksen toimintaa. Keskus on osa valtakunnallista LUMA-keskus Suomi -verkostoa, jonka tavoitteena on innostaa ja kannustaa lapsia ja nuoria LUMA-aineiden (luonnontieteet, matematiikka, ympäristöoppi ja teknologia) opiskeluun ja harrastamiseen uusimman tiede- ja teknologiakasvatuksen avulla.
Vuonna 2022 LUMA on erityisen ajankohtainen, sillä Suomen opetus- ja kulttuuriministeriö julkaisi vuoden 2021 lopussa Suomen LUMA-strategian vuodelle 2030. Strategian viesti on selkeä: LUMA-osaamisen tasoa tulisi parantaa sekä yksilön hyvinvoinnin että yhteiskunnallisen kehityksen tukemiseksi.
Olemme valinneet juttusarjaan aiheita, joiden avulla Dimensio-verkkolehden seuraajat voivat laajentaa ja syventää LUMA-osaamistaan ja hyödyntää juttuaiheita LUMA-aineiden opetuksessa. Toivomme antoisia lukuhetkiä ja voimia arkeen sekä juhlaan vuodelle 2022.
Terveisin: Itä-Suomen yliopiston LUMA-keskuksen väki
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista.







