Ideoita Integraalipäivien oppituntisuunnitelmista

Integraalipäivillä suunnitellaan matematiikan oppitunteja kouluihin tai kerhoihin matematiikan tutkijoiden pitämien esitelmien pohjalta. Tässä kirjoituksessa esitellään Integraalipäivillä kehiteltyjä oppitunteja. Lue juttu ja saa uusia ideoita omiin oppitunteihisi!

Integraalipäivät on viikonlopun mittainen tapahtuma, joka kokoaa yhteen matematiikan opettajia, opiskelijoita ja tutkijoita niin peruskouluista, toiselta asteelta kuin korkeakouluistakin. Oppituntien suunnittelun lisäksi tapahtumassa vaihdetaan ajatuksia matematiikasta ja matematiikan opetuksesta sekä vietetään viikonloppu innostavassa seurassa. Mallia tapahtumaan on otettu Ruotsin Kleindagarneista. Magnus Ehrnroothin säätiö rahoittaa Integraalipäiviä ja täten tapahtuma on osallistujille maksuton. Seuraavat Integraalipäivät pidetään 18.-20.11.2022 Scandic Tampere Koskipuistossa. 

Tähän mennessä pidetyillä Integraalipäivillä on suunniteltu yhteensä 11 oppituntia. Ne ovat saatavilla Integraalipäivien kotisivuilla, useimmat CC BY 4.0 -lisenssillä varustettuina. Eniten oppitunteja on lukiolaisille, mutta niitä löytyy myös peruskoululaisille ja ammatillisiin oppilaitoksiin. Useammassa oppitunnissa on elementtejä monialaisiin opintokokonaisuuksiin, kuten vaikkapa taiteen ja matematiikan yhdistämiseen. 

Alla on kuvattu tarkemmin Integraalipäivillä kehiteltyjä oppitunteja. Vaikka mikään niistä ei sellaisenaan sopisi omaan opetukseen, saattaa niistä löytyä yksittäisiä vinkkejä omiin oppitunteihin. Esimerkiksi valokuvien ja videoiden matematiikan oppitunnista saa yhden vastauksen kysymykseen ”Mihin neliöjuurta tarvitaan?”. (Vastaus: ”Valokuvan vaalennukseen.”)

Fraktaalien matematiikkaa

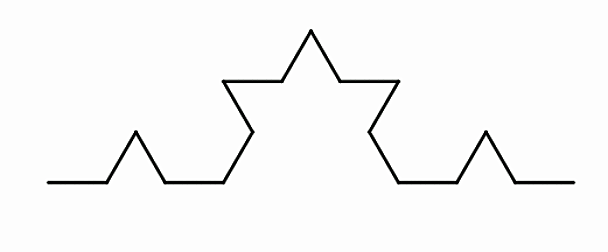
Anne-Maria Ernvall-Hytösen, Alli Huovisen, Ville Saarikiven, Teemu Tasasen ja Juha Vartiaisen suunnittelemassa oppitunnissa tutustutaan fraktaaleihin ja toistorakenteisiin. Se on suunnattu ensisijaisesti lukiolaisille (MAA11-moduuli), mutta sopii myös yläkouluun. Oppitunnin aluksi kukkakaalin avulla havainnollistetaan, mikä fraktaali on ja pohditaan, minkälaista toistuvuutta osallistujat ovat nähneet. Fraktaaleihin tutustumista jatketaan Kochin lumihiutalekäyrän avulla. Tunnin päätehtävänä on joko laatia fraktaalipuun piirtämiselle pseudo- tai ohjelmakoodi tai Sierpinskin maton ominaisuuksiin tutustumista. Lopuksi todetaan, etteivät kaikki fraktaalit ole sellaisia, jotka saadaan toistamalla samaa operaatiota.

Johdantoa suurten lukujen lakiin

Eeli Tammisen, Christian Webbin, Mikko Jaskarin, Eeva Pyrhösen, Heli Virtasen, Juha-Matti Huuskon ja Sakari Salosen kehittämässä oppitunnissa tutustutaan suurten lukujen lakiin, sen merkitykseen tilastojen käsittelyssä sekä aineistojen keräämiseen, käsittelyyn ja simulointiin. Kohderyhmänä ovat lukion 3. vuosikurssin oppilaat. Johdantona suurten lukujen lakiin toimii nopanheiton silmälukujen odotusarvon tutkiminen. Ttähän on annettu apuna Excel-tiedosto). Tämän jälkeen todistetaan suurten lukujen laki. Lopuksi tutustutaan hypergeometriseen jakaumaan karkkien lukumäärän avulla, tutkitaan jakaumaa ja visualisoidaan sitä Geogebralla.

Kokonaisluvut ja murtoluvut

Henri Anttilan, Harriet Beaverin, Leila Kokon ja Riikka-Liisa Vaaran kehittelemällä oppitunnilla pohditaan jaollisuutta, lukujen suuruutta sekä kokonaislukujen ja murtolukujen määrää. Tunti on suunnattu peruskoulun 7. luokan oppilaille. Oppitunti koostuu kolmesta tehtävästä, joita tehdään pienryhmissä, ja tehtävien läpikäynnistä. Yhtenä tehtävänä on esimerkiksi pyrkiä keksimään mahdollisimman suuri lukua 1 pienempi murtoluku.

Kvanttilaskentaan tutustuminen Groverin algoritmin kautta

Åsa Hirvosen, Otso Huuskan ja Heli Virtasen suunnittelemalla oppitunnilla tutustutaan kvanttilaskennan perusteisiin sekä Groverin hakualgoritmiin. Se on suunnattu lukion viimeisen vuoden opiskelijoille (esim. MAA11-moduuli). Oppitunti koostuu teoriaosioista ja näitä seuraavista tehtävien ratkaisemisesta.

Liikenneverkkojen paikallisten pullonkaulojen hahmottaminen verkon kaarevuuden käsitteen kautta

Otso Huuskan, Markku Leinon ja Ville Tilviksen laatimalla oppitunnilla tutustutaan verkon, sen osien ja kaarevuuden käsitteisiin. Oppitunti on suunniteltu lukion matematiikkakerhoon. Eteneminen tapahtuu lyhyisiin teoriaosuuksiin tutustumisesta ja niiden pohjalta tehtävien ratkaisemisesta.

Polynomeista algebrallisiin ja transkendenttisiin lukuihin

Anne-Maria Ernvall-Hytösen, Mats Gyllenbergin, Otso Huuskan, Terhi Juntusen, Ossi Maunon, Topi Tirkkosen ja Iivari Ylisen laatimalla oppitunnilla käsitellään polynomeja ja niiden avulla siirrytään algebrallisiin ja transkendenttisiin lukuihin. Kohderyhmänä ovat lukiolaiset (MAA2-moduulin loppupuolta opiskelevat tai kertaavat). Materiaali etenee lyhyistä teoriaosioista tehtäviin. Polynomien osalta harjoitellaan polynomien nollakohtien etsimistä sekä polynomien muodostamista nollakohtien avulla. Tämän jälkeen esitellään algebrallisten ja transkendenttisten lukujen käsitteet, huomataan, että on olemassa ei-algebrallisia lukuja ja tutustutaan muutamaan tällaiseen lukuun. Oppimateriaalin lopussa on lisämateriaalia kiinnostuneille.

Symmetrioita, laatoituksia ja taidetta

Anne-Maria Ernvall-Hytösen, Terhi Juntusen, Jarkko Karin ja Ville Saarikiven laatimasta, symmetrioita, laatoituksia sekä matematiikan ja taiteen yhteyttä käsittelevästä materiaalista on kaksi versiota: yleisempi lukiolaisille suunnattu versio sekä yksinkertaisempi yläkoululaisten versio. Opettajalle on myös tarjottu kalvopaketti, jota hän voi käyttää teorian esittelyyn. Suurimmalta osin kumpikin oppitunti koostuu tehtävien ratkaisemisesta. Materiaaleissa on mukana haastavampia tehtäviä, jotka on tarkoitettu ylöspäin eriyttämiseen.

Tartuntatautien matematiikkaa

Viivi Aaltosen, Peppiina Laakson, Helena Konttisen ja Mats Gyllenbergin laatimalla oppitunnilla tutustutaan tartuntatautien leviämiseen ja mallintamiseen. Kohderyhminä ovat alakoululaiset, yläkoululaiset ja lukiolaiset (sopii useampaan moduuliin). Tunti alkaa tartuntatautia mallintavalla pelillä, eri kohderyhmille omansa. Pelissä sairastuneiden lukumäärä kirjataan ylös, sitä tutkitaan ja eri pelikerroilla saatuja lukumääriä havainnollistetaan taulukoin ja kuvioin. Yläkoululaisten ja lukiolaisten kanssa tutustutaan lopuksi erilaisiin tartuntamäärää kuvaaviin malleihin, kuten eksponentiaaliseen malliin, sekä pohditaan, mitkä asiat vaikuttavat tartuntamääriin.

Tyypilliset ja epätyypilliset havainnot

Pauliina Ilmosen, Hannu Huhtalon, Armi Hopea-Mannerin, Ulla Mäkilän ja Mika Koskenojan laatima, yläkoululaisille, lukiolaisille ja ammatillisen koulutuksen oppilaille suunnattu oppimateriaali koostuu kahdesta oppitunnista. Ensimmäisellä oppitunnilla tutustutaan tilastotieteen keskeisiin käsitteisiin ja tuloksiin, kuten satunnaismuuttujiin, populaatioon ja normaalijakaumaan. Oppitunnin suositeltu sisältö vaihtelee kohderyhmittäin. Toisella oppitunnilla sovelletaan ensimmäisellä tunnilla opittuja asioita. Esimerkkinä on annettu Kouvolan Anjalan heinäkuun lämpötilojen tutkiminen (keskiarvo, keskihajonta, minimi jne.) Excel-ohjelmaa käyttäen.

Vaikeat ongelmat, riittävän hyvän ratkaisun etsiminen, löytäminen ja hyväksyminen

Tarja Ylivuoren, Aleksi Karhun, Mats Gyllenbergin ja Havu Miikosen laatimalla oppitunnilla tutustutaan muutamiin strategioihin, joita voidaan käyttää vaikeiden matemaattisten ongelmien ratkaisemisessa, sekä hahmottamaan näiden ongelmien ratkaisuavaruuksien suuruutta. Se on suunnattu yläkoululaisille, lukiolaisille ja ammatillisen koulutuksen oppilaille. Oppitunti koostuu neljästä toiminnallisesta pisteestä, joissa kussakin pohditaan yhtä ongelmaa, esimerkiksi kappamatkustajan ongelmaa. Lopuksi vedetään eri ryhmien havainnot yhteen ja pohditaan niitä (syvyys ryhmän mukaan). Oppituntisuunnitelma sisältää myös opettajan kalvopaketin.

Valokuvien matematiikkaa

Topi Törmän, Oona Laakson, Birgitta Nenonen-Anderssonin ja Heli Virtasen suunnittelemalla oppitunnilla käsitellään harmaasävykuvaa, värikuvan esittämistä numeroina sekä opettajan valinnan mukaan joko yhteen- ja kertolaskujen yhteyttä valokuviin tai valokuvan vaalennusta neliöjuuren avulla. Oppitunti on suunnattu yläkoululaisille ja lukiolaisille (esim. MAA11-moduuli).

Kuhunkin aiheeseen tutustutaan Youtube-videon avulla, ja tämän jälkeen aiheesta tehdään tehtäviä. Vaihtoehtoisissa kokonaisuuksissa tehtävänä on kokeilla itse, miten valittu operaatio vaikuttaa kuviin. Tätä varten annetaan esimerkkinä MATLAB-koodit.