Kvanttimekaniikan peruskysymyksiä: teorian tulkinnoista

Kvanttimekaniikan toinen vuosisata käynnistyy 2025 [1] ja sen ensimmäisestä vuosikymmenestä odotetaan kvanttiteknologian, kvanttilaskennan ja kvanttitietokoneiden läpimurtoa, jonka uskotaan auttavan muun muassa valtavaa laskentatehoa vaativien monimutkaisten molekyylirakenteiden tutkimusta sekä tekoälysovellusten kehittämistä. [2] Kvanttimekaniikan huikean menestystarinan, ja kvanttiteknologialle asetettujen odotusten valossa voi vaikuttaa hämmentävältä, että teorian tulkinnasta ei kuitenkaan ole päästy yksimielisyyteen. Hämmennystä ei välttämättä vähennä alan populaarikirjallisuus, josta voi helposti saada hyvinkin harhaanjohtavan kuvan ongelman luonteesta ja sen ratkaisuvaihtoehdoista. Vielä vähemmin asiaa palvelee eräiden tulkintakoulukuntien lähes dogmaattiset julistukset oman tulkinnan ensisijaisuudesta.

Teorian aito todennäköisyysluonne ja kvanttikietoutuminen sekä siihen liittyvä mittausongelma ovat tulkintakiistojen keskeisimpiä syitä, sillä ne problematisoivat esimerkiksi fysikaalisten suureiden arvoista puhumisen paitsi ennen suureen mittausta, voiko suureella olla arvo jonka mittaus paljastaa, niin myös sen mittauksen jälkeen, voidaanko mittaustuloksesta päätellä mitatun suureen arvo.

Kvanttimekaniikan sovellusten kannalta on kuitenkin ilmeisen riittävää, että teorian keskeinen matemaattinen rakenne tunnetaan hyvin ja sen minimitulkinnasta ollaan oleellisesti yksimielisiä. On myös tärkeää huomata, että kvanttimekaniikan ominaisimmat piirteet, kuten puhtaiden tilojen superpositiot, tiettyjen suureiden yhteismittausten puute ja kvanttikietoutuminen on pystytty valjastamaan uusiksi voimavaroiksi, joihin kvanttiteknologian uudet odotukset juuri keskeisesti tiivistyvät.

Tällaista kehitystä ohjaavat usein intuitiiviset ajatukset, jotka eivät välttämättä rajoitu minimitulkintaan, jolloin voidaan kysyä missä määrin nämä ajatukset ovat sopusoinnussa itse teorian kanssa. Lisäksi, jos pyrimme muodostamaan yhtenäistä kuvaa (fysikaalisesta) maailmasta niin kuin se näyttäisi hahmottuvan kvanttimekaniikasta käsin, niin emme myöskään voi kokonaan välttää ottamasta kantaa teorian tulkintaan. [3]

Kirjansa Tiede ja ihmisjärki (Otava, 1987) luvussa Ymmärrettävyyden kriisi Georg Henrik von Wright viittaa juuri kvanttimekaniikan aitoon todennäköisyysluonteeseen sekä kvanttikietoutumiseen piirteinä joissa ”fysiikan käsitettävyyden klassiset mallit näyttävät luhistuneen”, ja näkee ne ilmauksina tarpeesta ”uusien tieteellisen käsitettävyyden perusmallien etsinnästä”. Loogiset ristiriidat kuten Einsteinin-Podolskyn-Rosenin paradoksi (K2.4.2) [4] sekä mittausongelma (jakso 2.2.3) ovat kuuluisia esimerkkejä tällaisesta luhistumisesta kun taas paradoksien purku ohjaa ajatuksia mahdollisille uusille urille. [5]

Tieteellisellä käsittämisellä tai ymmärtämisellä on monia muotoja, asteita ja vivahteita, ymmärtäminen riippuu asiayhteydestä sekä käytössä olevista teorioista ja muuttuu ajan myötä. [6] Tässä kirjoituksessa ymmärtämistä hahmotellaan kvanttimekaniikan loogis-matemaattis-käsitteellisen viitekehyksen puitteissa, jolloin minimivaatimus teorian tulkinalle on sen sisältämien ajatusten koherenssi ja ristiriidattomuus itse teorian perusrakenteiden kanssa.

Tämä kirjoitus jatkaa kahta aiempaa kvanttimekaniikan peruskysymyksiä esitteleviä Dimensio -artikkeleita K1 Kvanttimekaniikan peruskysymyksiä: Yhteismittauksista ja epätarkkuuksista (18.2.2021) ja K2 Kvanttimekaniikan peruskysymyksiä: Yhdistetyt systeemit ja kvanttikietoutuminen (17.6.2021) teorian tulkintaongelman lähtökohtien sekä eräiden tämän ongelman ratkaisemiseksi hahmoteltujen näkökulmien esittelyllä.

Kuten artikkelissa K1 on jo tuotu esille, kvanttimekaniikka, kuten mikä tahansa fysiikan teoria, voidaan esittää usealla eri tavalla eikä teorian loogis-matemaattista rakennetta ja perustulkintaa voida antaa täysin irrallaan teorian tulkinta-ongelmasta. Koska teorian rakenteesta ja sen perustulkinnasta vallitsee kuitenkin laaja yksimielisyys, otamme lähtökohdaksi edellisissä artikkeleissa kuvatun perusteorian. Palautamme kirjoituksen aluksi, luku 1, lyhyesti mieleen tämän rakenteen ja tulkinnan. Luvussa 2 esittelemme yksityiskohtaisemmin kvanttimekaniikan tulkintaongelman lähtökohdan: aidon todennäköisyysluonteen epäobjektiivisuuskysymyksen, jakso 2.1, sekä mittausteorian objektivointiongelman, jakso 2.2. Luku 3, Kvanttimekaniikan tulkinnoista, esittelee aluksi kvanttimekaniikan Kööpenhaminan tulkinnan pääpiirteitä, jakso 3.1, Bohrin ja Heisenbergin (3.1.1) sekä von Neumannin (3.1.2) keskeisten ajatusten kautta, edeten jaksossa 3.2 monimaailma- sekä modaalitulkintojen katsauksiin (3.2.1 ja 3.2.2). Jaksossa 3.3 esitellään lyhyesti ympäristön mahdollista osuutta mittausongelman ratkaisemiseksi ns. dekoherenssi-ilmiön avulla, josta esimerkkinä kvanttidarwinismiksi nimetty tulkintahahmotelma (3.3.1). Samaan kategoriaan kuuluvat erilaiset spontaanin lokalisoinnin mallit tai teoriat (3.3.2), joiden tavoitteena on modifioida kvanttimekaniikkaa yleisemmäksi teoriaksi, joka tuottaisi mikroskooppisella tasolla kvanttimekaniikan ja makroskooppisella tasolla klassisen mekaniikan ennusteet. Jakso 3.4 esittelee lyhyesti viime aikoina mediajulkisuuttakin saaneet kvanttimekaniikan relationaalisen tulkintahahmotelman sekä bayesiläiselle subjektiiviselle todennäköisyyskäsitteelle perustuvan QBismin.

1. Perusrakenne ja minimitulkinta

Artikkeleissa K1 ja K2 kvanttimekaniikan matemaattista muotoilua hahmoteltiin ja perusteltiin tarkastelemalla fysikaalisen kokeen yleistä periaatteellista asetelmaa kolmivaiheisena prosessina, jossa fysikaalinen systeemi $\mathcal{S}$ preparoidaan mittausta varten halutulla tavalla, suoritetaan aiottu mittaus ja rekisteröidään tulos. Asettamalla kokeelle tilastollisen kausaliteetin vaatimus päädytään fysikaalisen systeemin todennäköisyysteoreettiseen kuvaukseen, joka rakentuu (lähtökohtaisesti abstrakteille) fysikaalisten suureiden (mittausten ekvivalenssiluokkien) $O\in \boldsymbol{O}$ ja tilojen (preparointien ekvivalenssiluokkien) $s\in \boldsymbol{S}$ määrittelemille todennäköisyysmitoille $p^O_s: \mathcal{A}\to[0,1]$, luvun $p^O_s(X)$ antaessa todennäköisyyden sille, että suureen $O$ mittaus tuottaa tuloksen testijoukosta $X\in \mathcal{A}$ kun systeemi on valmistettu tilaan $s$. [7] Kun joukoille $\boldsymbol{O}$ ja $\boldsymbol{S}$ asetetaan ehtoja, teorian postulaatit, teorian $(\boldsymbol{S},\boldsymbol{O},p)$ rakenne tarkentuu. Näin saadaan myös hyvin näkyviin minkälaiset olettamukset (postulaatit) erottavat klassisen ja kvanttiteorian toisistaan. Kuten kirjoituksen K1 luvussa 2 on kerrottu tämän lähestymistavan puitteissa on mahdollista muotoilla joukko pääasiassa fysikaalisesti motivoituja olettamuksia jotka kiinnittävät teorian kvanttimekaniikaksi, kompleksisen separoituvan ääretönulotteisen Hilbertin avaruuden operaattoriteoriaksi; tarkemmin ilmaistuna, tilat $s\in \boldsymbol{S}$ identifioituvat tämän avaruuden $\mathcal{H}$ tiettyinä (positiivisina jäljen yksi) operaattoreina $\rho $, $\rho \in \boldsymbol{S}(\mathcal{H})$, ja suureet $O\in \boldsymbol{O}$ tiettyinä (efektiarvoisina) mittoina $\mathcal{A}\ni X\mapsto \mathsf{E} (X)\in \boldsymbol{E}(\mathcal{H})$ niin, että luku $p^\mathsf{E}_\rho(X)$ määräytyy ns. Bornin lausekkeesta $p^\mathsf{E}_\rho(X)= tr [\rho \mathsf{E}(X)]$. Sanomme myös, että $\mathcal{S}$ on aito kvanttisysteemi, jos jokainen efekti $E\in \boldsymbol{E}(\mathcal{H})$ (siis ehdot $0\leq E\leq I$ toteuttava operaattori) on muotoa $E=\mathsf{E}(X)$ jollekin fysikaaliselle suureelle $\mathsf{E}$ ja testijoukolle $X$.

Kuten artikkeleissa K1 ja K2, niin myös tässä kirjoituksessa viitataan matemaattisiin käsitteisiin ja tuloksiin. Lukijan kannalta olennaista on kuitenkin vain se, että fysikaalisen systeemin kvanttimekaniikan mukaisessa kuvauksessa käytetyillä peruskäsitteillä tila ja suure sekä niiden määrittelemillä todennäköisyysmitoilla on täsmälliset matemaattiset rakenteet; niiden yksityiskohtainen tunteminen ei ole tässä tarpeen. On ehkä paikallaan myös korostaa sitä, että teorian kehittelyn tässä vaiheessa sen keskeiset fysikaaliset käsitteet ovat ensisijaisesti vain intuitiivisen ymmärryksen varassa. Niiden tarkempi sisältö täsmentyy teorian jatkokehittelyn myötä, erityisesti kun tutkitaan fysikaalisen systeemin käyttäytymistä avaruuden ja ajan symmetriamuunnoksissa, kuten paikka- tai aikasiirrot, kierrot, ja nopeussysäykset.

Kvanttimekaniikan matemaattis-käsitteellinen esitys on tässä perusteltu ns. operationaalisen lähestymistavan puitteissa analysoimalla kokeen yleistä rakennetta tilastollisen kausaliteetin periaatteen avulla. On kuitenkin huomattava, että näin syntyvä kvanttimekaniikan perusrakenne ei riipu tästä lähestymistavasta; sitä voidaan perustella eri tavoin ja se voidaan myös ottaa, ja usein otetaankin, käyttöön suoraan ikään kuin aksiomaattisesti: fysikaalisen systeemin (tai tietomme siitä) kuvaus perustetaan abstraktille Hilbertin avaruus -teorialle yllä kuvatuin perusrakentein. Teorian minimitulkinnalla tarkoitetaan juuri sitä, että tilojen ja suureiden (tai mittausten) määrittelemille todennäköisyysmitoille annetaan mittaustulostodennäköisyys- tai mittaustulostilastotulkinta. Tiettyjä poikkeuksia lukuun ottamatta tämä rakenne ja tulkinta on kvanttimekaniikan varsinaisten tulkintakysymysten yhteinen lähtökohta.

Kertaus 1. Puhtaat tilat ja tarkat efektit. Tilajoukon konveksi rakenne mahdollistaa erottelun puhtaiden ja sekoitettujen tilojen välillä. Tila on puhdas jos sitä ei voida lausua muiden tilojen (aitona) konveksikombinaationa (K1, luku 2). Tällaiset tilat ovat maksimaalisen informaation tiloja siinä mielessä, että niiden valmistaminen (systeemin preparointi) ei sisällä minkäänlaista (teorian puitteissa kuvattavissa olevaa) epätäydellisyyttä. Samalla tavalla efektijoukon konveksi rakenne johtaa efektien luonnolliseen jakoon, nyt termeinä tarkat ja sumeat efektit. Sekä tilojen että efektien tapauksessa sama jako saadaan myös algebrallisesti: tila $\rho \in \boldsymbol{S}(\mathcal{H})$ on puhdas jos ja vain jos se on idempotentti (eli projektio), $\rho^2=\rho$, ja efekti $E\in \boldsymbol{E}(\mathcal{H})$ on tarkka jos ja vain jos se on idempotentti, $E^2=E$. Efektien jako johtaa myös suureiden jakoon tarkkoihin ja sumeisiin suureisiin. Kuten puhtaat tilat niin myös tarkat suureet erottuvat mahdollisten mittaustensa osalta: tarkka suure voidaan mitata ns. toistavalla mittauksella, mittauksella jonka välitön toisto tuottaa varmuudella jo saadun tuloksen (ks. jakso 2.2).

Kertaus 2. Puhtaiden tilojen superpositiot. Kvanttimekaniikan tilajoukon $\boldsymbol{S}(\mathcal{H})$ eräs erityispiirre on puhtaiden tilojen superpositiot: mitkä tahansa kaksi (tai useampaa) puhdasta tilaa voidaan aina superponoida (yhdistää) uusiksi puhtaiksi tiloiksi, ja mikä tahansa puhdas tila voidaan aina lausua (monella eri tavalla) joidenkin muiden puhtaiden tilojen superpositiona. Sanomme, että puhdas tila $\rho$ on puhtaiden tilojen $\rho_1$ ja $\rho_2$ superpositio jos se on näiden tilojen välissä seuraavassa todennäköisyysteoreettisessa mielessä: kaikilla tarkoilla efekteillä $P$, jos efektin $P$ todennäköisyys tiloilla $\rho_1$ ja $\rho_2$ on nolla, ts. $tr[\rho_1P]=tr[\rho_2P]=0$, niin sen todennäköisyys tilalla $\rho$ on myös nolla, ts. $tr[\rho P]=0$. [8] Koska puhtaat tilat $\rho$ ovat yksiulotteisia projektioita ja vastaavat siten vektoriavaruuden $\mathcal{H}$ yksiulotteisia aliavaruuksia $[φ]=\{cφ\,|\,c\in \mathbb{C} \}$, missä $φ\in \mathcal{H}$ on yksikkövektori, niin nähdään, että puhdas tila $\rho$ on puhtaiden tilojen $\rho_1$ ja $\rho_2$ superpositio tarkalleen silloin kun tilaa $\rho$ vastaava yksikkövektori $φ$ voidaan lausua puhtaisiin tiloihin $\rho_1$ ja $\rho_2$ liittyvien yksikkövektoreiden $φ_1$ ja $φ_2$ lineaarikombinaationa $c_1φ_1+c_2φ_2$. Jos tilat $\rho_1$ ja $\rho_2$ ovat keskenään kohtisuorat, $tr[\rho_1\rho_2]=0$, ts. $⟨ φ_1 |φ_2 ⟩=0$, niin kertoimien $c_1$ ja $c_2$ itseisarvojen neliöiden summa on yksi, $|c_1|^2+|c_2|^2=1$. (Ks. K1 Taustatietoa 3)

2. Tulkintaongelman lähtökohta

Kvanttimekaniikan aito todennäköisyysluonne ja mittausongelma määrittelevät ja viitoittavat selkeimmin teorian tulkintaongelman ja sen mahdollisia ratkaisulinjoja. Esittelemme seuraavassa teorian nämä erityispiirteet.

2.1. Aito todennäköisyys. Kvanttimekaniikan todennäköisyysrakennetta ja sen erityispiirteitä esiteltiin melko laajasti jo artikkelissa K1, sen luvuissa 2 ja 4, joten toistan tässä vain esityksen kannalta oleellisimmat seikat. Palautetaan kuitenkin aluksi mieleen, että klassisen teorian tapauksessa kaikki todennäköisyysväittämät voidaan periaatteessa palauttaa oleellisesti yksikäsitteisellä tavalla 0-1 -arvoisiin todennäköisyyksiin, kuten yksinkertainen esimerkki 5/K1 osaltaan havainnollistaa. Yhtäpitävästi, millä tahansa fysikaalisella suureella, dynaamisella muuttujalla, on klassisen teorian mukaan joka hetki hyvin määritelty, mahdollisesti tuntematon arvo, joka voidaan periaatteessa (mittaamalla) määrittää systeemiä mitenkään muuttamatta. Klassisessa teoriassa todennäköisyysväittämiin joudutaan turvautumaan tyypillisesti vain epätäydellisen tiedon tai taidon tilanteissa.

Luku $p^\mathsf{E}_\rho(X)$ on todennäköisyys sille, että suureen $\mathsf{E}$ mittaus tilassa $\rho$ tuottaa tuloksen joukosta $X$. Tällaisessa lähestymistavassa varmuus on luonteeltaan tilastollista. Oletetaan yksinkertaisuuden vuoksi, että suure $\mathsf{E}$ on tarkka kaksiarvoinen suure, arvoina merkit $+$ ja $-$, $\mathsf{E} (\{+\}) =E_+, \mathsf{E}(\{-\})=E_-$, vastaten kyllä-ei -kokeen tuloksia. [9] Jos $p^\mathsf{E}_\rho(\{+\})=1$, niin tällöin suureen $\mathsf{E}$ mittaus tuottaa (probabilistisella) varmuudella kyllä-tuloksen. Tällöin voimme sanoa (eli ottaa ristiriidattomasti käyttöön puhetavan), että suureella $\mathsf{E}$ on tilassa $\rho$ arvo $+$; vaihtoehtoisesti, että fysikaalisella systeemillä on tässä tilassa kyllä-tulosta vastaava ominaisuus $E_+$. [10] Samoin, jos $p^\mathsf{E}_\rho(\{-\})=1$, niin sanomme, että systeemillä on tässä tilassa ominaisuus $E_-$. Yleisemmin, jos $p^\mathsf{E}_\rho(\{\pm \})\in\{0,1\}$, niin sanomme, että suure $\mathsf{E}$ on objektiivinen kyseisessä tilassa; sillä on tässä tilassa joko arvo $+$ tai arvo $-$; yhtäpitävästi, systeemillä on tässä tilassa joko ominaisuus $E_+$ tai ominaisuus $E_-$, ja systeemillä on se ominaisuus jonka todennäköisyys tässä tilassa on yksi.

Jokaista puhdasta tilaa $\rho$ kohti on olemassa kaksiarvoisia (tarkkoja) suureita $\mathsf{E}$, jotka ovat tässä tilassa objektiivisia, siis niillä on joko kyllä-arvo tai ei-arvo tässä tilassa. Mutta jokaista puhdasta tilaa $\rho$ kohti on olemassa myös runsaasti (ylinumeroituva määrä) muita (tarkkoja) kaksiarvoisia suureita $\mathsf{F}$, joille $0\ne p^\mathsf{F}_\rho(\{+\})\ne 1$, ja siis myös $0\ne p^\mathsf{F}_\rho(\{-\})\ne 1$. Sanomme, että suure $\mathsf{F}$ on epäobjektiivinen tällaisessa tilassa. On paikallaan korostaa, että termiä epäobjektiivinen käytetään tässä yllä määritellyssä mielessä, merkityksessä objektiivisesti määrittämätön, ei subjektiivisessa mielessä tuntematon. [11]

Olkoon systeemi puhtaassa tilassa $\rho$ ja olkoon $\mathsf{E}$ tässä tilassa epäobjektiivinen (tarkka kaksiarvoinen) suure. Suureen mittaus tuottaa nyt varmuudella jomman kumman tuloksista $+$ tai $-$. Tuloksia vastaavia todennäköisyyksiä $0 \ne p^\mathsf{E}_\rho(\{\pm\}) \ne 1$ ei kuitenkaan voi tulkita epätäydellisen preparoinnin tai epätarkan mittauksen aiheuttamaksi tiedon puutteeksi suureen tosiasiallisesta arvosta tässä tilassa. Suureen $\mathsf{E}$ arvoista puhuminen tässä tilassa on varsin ongelmallista, ehkä jopa merkityksetöntä, eikä mittaus voi paljastaa arvoa joka suureella nyt olisi. Tämä on kvanttimekaniikan aidon todennäköisyysluonteen eräs keskeinen ilmentymä.

Kvanttimekaniikan aito todennäköisyysluonne liittyy läheisesti puhtaiden tilojen superpositioesitykseen: puhdas tila jossa annettu suure on epäobjektiivinen voidaan lausua sellaisten puhtaiden tilojen superpositiona joissa kyseinen suure on objektiivinen. Tässä yhteydessä käytetään usein sellaista puhetapaa, että suureella olisi kyseisessä tilassa samanaikaisesti ikään kuin useampia eri arvoja, kaksiarvoisen suureen tapauksessa molemmat arvot. Puhetapaa käytetään erityisesti puhtaiden tilojen ns. vektori- tai ’aaltofunktio’ -esityksen yhteydessä (ks. Kertaus 2). Puhetapa tarkoittaa kuitenkin vain sitä, että suureen mittaus kyseisessä tilassa johtaa johonkin näistä ’samanaikaisesti mahdollista’ arvoista kyseisellä todennäköisyydellä. Tätä metaforaa suosivien tekstien yhteydessä joutuu joskus myös lukemaan, että tällaisessa tilan superpositioesityksessä systeemin tila ei olisikaan hyvin määritelty; näkökulma on kuitenkin virheellinen. Se, että annettu (kaksi- tai useampiulotteisen avaruuden) vektori (tai funktio) voidaan lausua kaksiulotteisessa vektori (tai funktio) -avaruudessa mielivaltaisen monella tavalla joidenkin muiden vektoreiden (funktioiden) lineaarikombinaationa ei tee tästä vektorista (funktiosta) epämääräistä.

Kun Max Born oli vuonna 1926 esittänyt alustavan muotoilunsa saaneelle uudelle kvanttimekaniikalle sen todennäköisyysteoreettista tulkintaa, [12] Albert Einstein ilmaisi Bornille osoittamassaan kirjeessään 4.12.1926 huolensa ja kritiikkinsä teorian saamasta kehityskulusta: “[t]he theory produces a good deal but hardly brings us closer to the secret of the Old One. I am at all events convinced that He does not play dice.” [13] Tästä Einsteinin kvanttimekaniikan todennäköisyysluonteen kritiikistä on muotoutunut häneen liitetty siivekäs lause ’Jumala ei heitä noppaa!’.

2.2. Mittausongelma. Kvanttimekaniikan aidon todennäköisyysluonteen johdosta fysikaalisten suureiden arvoista puhuminen ennen mittausta ei siis ole perusteltua lukuun ottamatta suureita jotka ovat objektiivisia tilassa, johon systeemi on preparoitu. Jos systeemi on tilassa $\rho$ ja mittaamme tässä tilassa jonkun epäobjektiivisen kaksiarvoisen suureen $\mathsf{E}$, niin mittaus tuottaa (probabilistisella) varmuudella jomman kumman tuloksista $\pm$ ja tuottaa kyseisen tuloksen todennäköisyydellä $0 \ne p^\mathsf{E}_\rho(\{\pm\}) \ne 1$. Onko mahdollista, että suureella $\mathsf{E}$ olisi mittauksen jälkeen mittaustuloksen osoittama arvo?

Mittaustulostodennäköisyystulkinta ei aseta mitään erityisiä ehtoja itse mittaustapahtumalle eikä sille mitä mitattavalle systeemille siinä tapahtuu; systeemi saattaa jopa muuntua toiseksi systeemiksi, esimerkiksi hajota osiin, tai kokonaan tuhoutua (menettää identiteettinsä) iskeytyessään havaintolevylle. Asetettu kysymys kuitenkin edellyttää että voimme puhua systeemistä myös mittauksen jälkeen. Tämä edellyttää sitä, että jokainen suure voidaan ainakin periaatteessa mitata myös systeemin identiteettiä muuttamatta tai sitä tuhoamatta. Tämä onkin kvanttimekaniikan mittausteorian lähtökohta ja se rakentuu sille luonnolliselle olettamukselle, että mittaustapahtuma, tai ainakin osa siitä, on kvanttimekaniikan alaan kuuluva fysikaalinen prosessi. [14] (Vastaava oletus on kvanttilaskennan taustalla.)

2.2.1. Mittaustapahtuma kvanttimekaniikassa. Intuitiivisesti ja yksinkertaistettuna, mittaustapahtumassa mitattava systeemi vuorovaikuttaa mittalaitteen kanssa ja mittalaitteen asteikolta luetaan mittauksen jälkeen saatu tulos. Oletamme nyt, että mittalaite, tai ainakin sen keskeinen osa, on kuvattavissa mittalaitteen tilojen ja suureiden, sekä niiden määrittelemien todennäköisyysmittojen avulla kvanttimekaniikan yleisten periaatteiden mukaisesti. Mittausteoriasta tulee näin osa yhdistettyjen systeemien kvanttiteoriaa omine erityiskysymyksineen. Yhdistettyjen systeemien teorian perusteita on esitelty artikkelissa K2, jota tässä esityksessä hyödynnetään. [15]

Systeemin $\mathcal{S}$ (Hilbertin avaruudella $\mathcal{H}$) suureen $\mathsf{E}$ mittaamiseksi tarvitsemme sopivan mittalaitteen $\mathcal{M}$ (Hilbertin avaruudella $\mathcal{K}$), vertailu- eli asteikkosuureen $\mathsf{Z}$, sekä mittauskytkennän eli systeemien $\mathcal{S}$ ja $\mathcal{M}$ välisen mittausvuorovaikutuksen. Lisäksi oletamme, että mittalaite on ennen mittausta valmistettu systeemistä $\mathcal{S}$ riippumattomasti alkutilaan, kiinteään valmiustilaan $\sigma \in \boldsymbol{S}(\mathcal{K})$. Jos systeemi $\mathcal{S}$ on valmistettu ennen mittausta tilaan $\rho \in \boldsymbol{S}(\mathcal{H})$, niin mittauskytkennän johdosta $\mathcal{S}$ ja $\mathcal{M}$ kietoutuvat toisiinsa; yhdistetyn systeemin $(\mathcal{S},\mathcal{M})$ mittausta edeltävä (kietoutumaton) tila $\rho \otimes \sigma$ muuntuu mittauskytkennän vaikutuksesta systeemin $(\mathcal{S},\mathcal{M})$ tilaksi $V(\rho \otimes \sigma)$ mittauksen jälkeen. Oletamme tässä yksinkertaisuuden vuoksi, että mittaus on ikään kuin hetkellinen, puhumme vain yhdistetyn systeemin tilasta ennen ja jälkeen mittauksen (jolloin mittausvuorovaikutus on jo lakannut). Mittauksen aiheuttamalle tilamuunnokselle $\rho \otimes \sigma \mapsto V(\rho \otimes \sigma)$, $\sigma$ kiinteä, on luonnollisia matemaattisia säännöllisyysehtoja mutta niiden yksityiskohtainen tunteminen ei ole tässä olennaista. Parin $(\mathcal{S},\mathcal{M})$ mittauksen jälkeisestä tilasta $V(\rho \otimes \sigma)$ voidaan kuitenkin aina määrittää yksikäsitteisellä tavalla sekä mitattavan systeemin että mittalaitteen mittauksen jälkeiset tilat. Merkitään näitä tiloja lyhyesti symboileilla $\rho^f$ ja $\sigma^f$, $f{=}$ final, (pitäen tarvittaessa mielessä, että esim. $\rho^f$ riippuu luonnollisesti koko kolmikosta $(\mathcal{K}, V, \sigma)$). Erityisesti, voimme siis seurata systeemin tilan muuntumista $\rho\mapsto\hat m(\rho)=\rho^f$ mittaustapahtumassa (kuten jaksossa K2.7).

Perusvaatimus sille, että mittalaite $\mathcal{M}$ (tarkemmin, sen Hilbertin avaruus $\mathcal{K}$), asteikkosuure $\mathsf{Z}$, alkutila $\sigma$, ja vuorovaikutus $V$ määrittelevät suureen $\mathsf{E}$ mittauksen on ns. kalibrointiehto: jos suureella $\mathsf{E}$ on tilassa $\rho$ probabilistisella varmuudella tietty arvo, niin asteikkosuureella $\mathsf{Z}$ on mittauksen jälkeen (probabilistisella varmuudella) vastaava arvo; kaikilla $\rho$ ja $X$, jos $p^\mathsf{E}_\rho(X) = 1$, niin $p^\mathsf{Z}_{\sigma^f}(X) = 1.$ Tarkkojen suureiden $\mathsf{E}$ tapauksessa tämä ehto on yhtäpitävä näennäisesti vahvemman todennäköisyyden reprodusointiehdon kanssa: kaikilla $\rho$ ja $X$, $p^\mathsf{E}_\rho(X)=p^\mathsf{Z}_{\sigma^f}(X)$. Yleisessä tapauksessa (tarkat ja sumeat suureet) tämä todennäköisyyden reprodusointiehto onkin mittauksen määrittelyehto ja teorian lähtökohtana on tulos jonka mukaan jokaista mitattavan systeemin suuretta kohti on olemassa tällaisia mittauksia. [16]

Suureen $\mathsf{E}$ mittaus $\mathsf{M}=(\mathcal{K},\mathsf{Z},\sigma,V)$ määrittelee paitsi systeemin $\mathcal{S}$ mittauksen jälkeisen tilan $\rho^f=\hat m(\rho)$, niin myös sen mittauksen jälkeisen ehdollisen tilan $\hat m_X(\rho)$, kunhan $p^\mathsf{E}_\rho(X) \ne 0$; tilan, joka (Kolmogorovin teorian mukaisesti) synnyttää ehdollisia todennäköisyyksiä: kaikilla systeemin $\mathcal{S}$ suureilla $\mathsf{F}$, luku $p^\mathsf{F}_{\hat m_X(\rho)}(Y)$ on todennäköisyys sille, että suureen $\mathsf{F}$ mittaus tuottaa tuloksen joukosta $Y$ ehdolla, että ensin tilassa $\rho$ suoritettu suureen $\mathsf{E}$ mittaus $\mathsf{M}$ johtaa asteikkosuureen $\mathsf{Z}$ lukemaan joukosta $X$ (vrt. K1.7). [17] (Tila $\hat m_\Omega(\rho)$, missä $\Omega$ on suureen $\mathsf{E}$ arvojoukko, on luonnollisesti sama kuin tila $\hat m (\rho)$; ks. K1.2). Ilman mittauksen tarkempaa spesifiointia tästä ei kuitenkaan voi vielä päätellä juuri mitään itse kysymykseemme nähden.

Fysikaalisen suureen mittaus voidaan toteuttaa monella eri tavalla. Voimme esimerkiksi yrittää mitata suure niin, että mittaus ’häiritsee’ mitattavaa systeemiä mahdollisimman vähän, esimerkiksi niin, että kaikki ne ominaisuudet, jotka systeemillä on (probabilistisella varmuudella) ennen mittausta (siis tilassa $\rho$) ja jotka ovat yhteensopivat (yhteismitattavissa) mitattavan suureen kanssa, ovat (probabilistisella varmuudella) systeemillä myös mittauksen jälkeen (siis tilassa $\rho^f$), vrt. K1.7. Tämä ehto tunnetaan mittauksen ihanteellisuusehtona. Mittaus voidaan myös yrittää toteuttaa niin, että sen välitön toisto tuottaisi (probabilistisella varmuudella) aina saman tuloksen. Edelleen, koska asteikkosuureen arvosta haluttaisiin päätellä mitattavan suureen arvo mittauksen jälkeen ja suureiden arvoista voidaan päätellä jotain vain tilojen avulla niin mittausvuorovaikutukselta on luonnollista vaatia, että se synnyttää vahvoja korrelaatioita paitsi kyseisten suureiden mahdollisten arvojen niin myös tilojen välille. Nämä vaatimukset voidaan muotoilla luonnollisella tavalla mittausteorian puitteissa ja ne ovat rajoituksia ensisijaisesti mittaukselle $\mathsf{M}$.

Tarkan kaksiarvoisen suureen tapauksessa vahva korrelaatioehto johtaa siihen, että tilassa $V(\rho \otimes \sigma)$ yhdistetyn suureen $\mathsf{E} \otimes \mathsf{Z}$ mahdollisista tulospareista $(+,+),(+,-),(-,+),(-,-)$ vain parit $(+,+)$ ja $(-,-)$ voivat toteutua ja ne toteutuvat todennäköisyyksillä $p^\mathsf{E}_\rho(\{+\})$ ja $p^\mathsf{E}_\rho(\{-\})$. Mittauksen toistavuusvaatimus puolestaan johtaa siihen, että mittalaitteen mittauksen jälkeinen tila $\sigma^f$ voidaan esittää muodossa

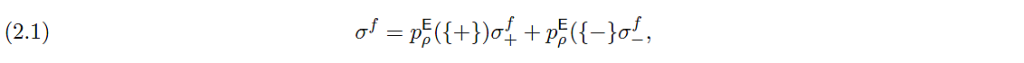
missä komponenttitilat $\sigma^f_\pm$ ovat asteikkosuureen $\mathsf{Z}$ ominaistiloja, toisin sanoen, näissä tiloissa asteikkosuureella on (probabilistisella varmuudella) arvot $\pm$ ja nämä tilat ovat muotoa $\sigma^f_\pm=p^\mathsf{E}_\rho(\{\pm\})^{-1}Z_\pm\sigma^fZ_\pm$. Tällöin myös mitattavan systeemin mittauksen jälkeisissä ehdollisissa tiloissa $\hat m_\pm(\rho)$ suureella $\mathsf{E}$ on (probabilistisella varmuudella) arvot $\pm$ ja tilalla $\hat m(\rho)$ on mittauksen antama hajotelmaa (2.1) vastaava luonnollinen hajotelma [18]

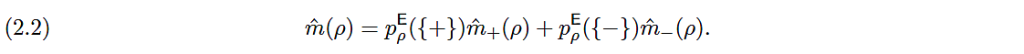
Vahva korrelaatio kytkee myös komponenttitilat $\sigma^f_+$ ja $\hat m_+(\rho)$ sekä $\sigma^f_-$ ja $\hat m_-(\rho)$ toisiinsa. Mittauksen ihanteellisuusvaatimus johtaa (tietyn teknisen lisäehdon myötä) vielä seuraavaan tarkennukseen: $\hat m_\pm(\rho)=p^\mathsf{E}_\rho(\{\pm\})^{-1} E_\pm\rho E_\pm$.

Esimerkki 1. Kuten edellä jo mainittiin, jokaiselle systeemin $\mathcal{S}$ suureelle $\mathsf{E}$ voidaan konstruoida todennäköisyyden reprodusointiehdon toteuttavia mittauksia $\mathsf{M}$. Eräs tavanomaisimmista malleista on kytkeä mitattava (tyypillisesti) tarkka suure mittalaitteen liikemäärään (vast. paikkasuureeseen) ja monitoroida kytkennän vaikutusta mittalaitteen paikkaan (vast. liikemäärään). Esimerkiksi, spin-$\frac 12$ objektin, kuten elektronin, spinin $z$-akselin suuntaisen komponentin Stern-Gerlach -tyyppinen mittaus toteutetaan niin, että elektronin spin (sisäinen vapausaste) kytketään $z$-akselin suuntaisella magneetilla elektronin liikemäärään (avaruudellinen vapausaste) kyseisen akselin suunnassa ja monitoroidaan eleketronin paikkasiirtymää kyseisessä suunnassa, siirtymä joko ’ylös’ tai ’alas’. Tällöin mittalaitteena toimii elektronin avaruudellinen liike, asteikkosuureena sen $z$-akselin suuntainen paikka. Mittalaitteen alkutila, elektronin avaruudellisen liikkeen alkutila, voidaan helposti valita niin, että ehdot (2.1) ja (2.2) toteutuvat.

2.2.2. Ongelma. Oletetaan nyt, että yllä kuvattu mittaus on toteutettu alkutiloina puhtaat tilat $\rho$ ja $\sigma$. Oletetaan ensin, että $\mathsf{E}$ on objektiivinen tässä tilassa, siis, että esimerkiksi $p^\mathsf{E}_\rho(\{+\})=1$. Mittauksen ihanteellisuuden takia kaksoissuureella $\mathsf{E} \otimes \mathsf{Z}$ on mittauksen jälkeisessä tilassa $V(\rho\otimes\sigma)$ (probabilistisella varmuudella) arvo $(+,+)$. Tällöin myös $\sigma^f=\sigma^f_+$ ja $\hat m(\rho)=\hat m_+(\rho)$ ovat puhtaita tiloja ja $V(\rho\otimes\sigma)$ on kietoutumaton tulotila $\hat m_+(\rho)\otimes\sigma^f_+$, jossa ihanteellisuuden takia jopa $\hat m_+(\rho)=\rho$. [19]

Oletetaan seuraavaksi, että $\mathsf{E}$ on epäobjektiivinen tilassa $\rho$, siis, että $0\ne p^\mathsf{E}_\rho(\{\pm\})\ne 1$. Vahvan korrelaation johdosta pari $(\mathcal{S},\mathcal{M})$ on nyt sellaisessa (puhtaassa) tilassa $V(\rho\otimes\sigma)$, jossa kaksoissuureen $\mathsf{E} \otimes \mathsf{Z}$ mahdollisista neljästä arvoparista vain arvoparien $(+,+)$ ja $(-,-)$ todennäköisyydet eroavat nollasta ja ne ovat $ p^\mathsf{E}_\rho(\{+\})$ ja $ p^\mathsf{E}_\rho(\{-\})$, vastaavasti. Kaksoissuure $\mathsf{E} \otimes \mathsf{Z}$ on siis epäobjektiivinen mittauksen jälkeisessä puhtaassa tilassa $V(\rho\otimes\sigma)$; ei voida sanoa että sillä olisi jompi kumpi arvopareista $(+,+)$ tai $(-,-)$, molemmat arvoparit ovat ’potentiaalisesti läsnä’ tässä tilassa; suureen $\mathsf{E} \otimes \mathsf{Z}$ mittaus tässä tilassa tuottaisi (probabilistisella) varmuudella jomman kumman näistä arvopareista.

Sama asiantila ilmenee mittalaitteen $\mathcal{M}$ mittauksen jälkeisessä (välttämättä sekoitetussa) tilassa $\sigma^f$, jossa $p^\mathsf{Z}_{\sigma^f}(\{\pm\})=p^\mathsf{E}_\rho(\{\pm\})$. Vaikka tilalla on mittauksen tuottama luonnollinen hajotelma (2.1) niin sen mikä tahansa hajotelma (joita on ylinumeroituva määrä) tuottaa tarkalleen samat todennäköisyydet; tilaa $\sigma^f$ ei voida tulkita episteemisesti hajotelman (2.1) avulla niin, että tässä tilassa mittalaite $\mathcal{M}$ itse asiassa olisi jommassa kummassa komponenttitilassa $\sigma^f_\pm$, painokertoimien $p^\mathsf{E}_\rho(\{\pm\})$ kuvatessa tiedon puutetta mittalaitteen tosiasiallisesta tilasta. Sama pätee sanasta sanaan systeemin $\mathcal{S}$ mittauksen jälkeiselle tilalle.

Yllä kuvattua ongelmaa voidaan vielä tarkentaa tarkastelemalla vaatimusta asteikkosuureen $\mathsf{Z}$ objektiivisuudesta mittalaitteen mittauksen jälkeisessä tilassa $\sigma^f$, siis vaatimusta että asteikkosuureella olisi jompi kumpi mahdollisista arvoistaan, todennäköisyyden $p^\mathsf{E}_\rho(\{\pm\})$ ilmaistessa tiedon epävarmuutta asteikkosuureen tosiasiallisesta arvosta. Tällä vaatimuksella on kaksi ilmeistä seuraamusta. Jos näin olisi, niin välttämättä myös (triviaalilla) kaksoisuureella $I \otimes \mathsf{Z}$ olisi (probabilistisella varmuudella) vastaava arvo tilassa $V(\rho\otimes\sigma)$. Tämä tarkoittaisi sitä että myös tilan $V(\rho\otimes\sigma)$ pitäisi olla (kaikilla $\rho$) ehdollista muotoa

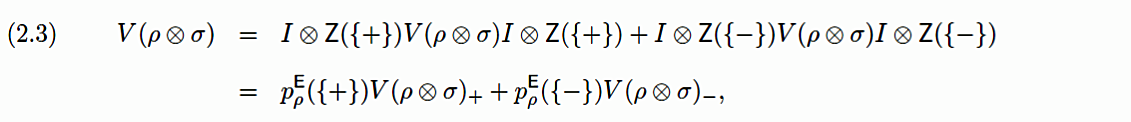
missä (normitetut) tilat $V(\rho\otimes\sigma) \pm = I \otimes \mathsf{Z}(\{\pm\})V(\rho\otimes\sigma) I \otimes \mathsf{Z}(\{\pm\})/p^\mathsf{E}_\rho(\{\pm\})$. [20] Jos tila $\sigma$ on puhdas, niin tämä ei luonnollisestikaan ole mahdollista (sillä $V$ on unitaarinen). Mittalaitteen alkutila voidaan kuitenkin valita myös sekoitetuksi tilaksi [21] (ja asteikkosuure sumeaksi suureeksi). Voisiko tämä (nämä) valinta (valinnat) johtaa asteikkosuureen objektivoinnin välttämättömän ehdon (2.3) toteutumiseen? Vastaus on kielteinen: [22]

ei ole olemassa sellaista suureen $\mathsf{E}$ mittausta $\mathsf{M}$, jossa mittalaite $\mathcal{M}$ olisi aito kvanttimekaaninen systeemi, mittauskytkentä $V$ unitaarinen, ja joka toteuttaisi ehdon (2.3).

2.2.3. Mittausparadoksi. Voimme nyt muotoilla mittausongelman loogisena ristiriitana sen keskeisten olettamusten ja tavoitteiden yhteensopimattomuutena. Samalla ristiriita osoittaa miten ongelma mahdollisesti voitaisiin ratkaista. Sen muotoilemiseksi otamme käyttöön seuraavat lyhenteet:

(PR) $\mathsf{M}=(\mathcal{K}, \mathsf{Z}, \sigma, V)$ on suureen $\mathsf{E}$ mittaus (todennäköisyyden reprodusointiehdon mielessä).

(QS) $\mathcal{S}$ on aito kvanttisysteemi.

(QM) $\mathcal{M}$ on aito kvanttisysteemi.

(U) Mittauskytkentä $V$ on unitaarinen (ks. alaviite 16).

(O1) Mittalaitteen mittauksen jälkeinen tila voidaan esittää muodossa (2.1).

(O2) Parin $(\mathcal{S},\mathcal{M})$ mittauksen jälkeinen tila voidaan esittää muodossa (2.3).

Kvanttimekaniikan mittausteorian mukaan jokaiselle suureelle $\mathsf{E}$ voidaan konstruoida ehdot (PR), (QS), (QM), ja (U) toteuttavia mittauksia. Lisäksi mittalaitteen mittauksen jälkeiselle tilalle $\sigma^f$ saadaan hajotelma (2.1), eli ehto (O1) toteutuu aina kun mittaus valitaan toistavaksi. Toisaalta, ehto (O2) on välttämätön, jotta asteikkosuure olisi objektiivinen mittauksen päätyttyä. Mutta

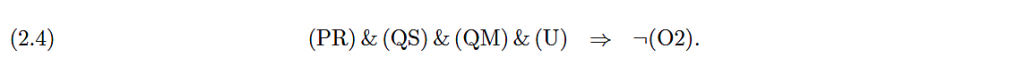
Kvanttimekaniikan puitteissa, yllä luetelluin ehdoin, ei ole mahdollista perustella että asteikkosuureella ja niin muodoin mitattavalla suureella olisi mittauksen jälkeen hyvin määritelty, mahdollisesti tuntematon arvo. Tämä dilemma tunnetaan kvanttimekaniikan mittausongelmana. Sen ratkaisemiseksi tai eliminoimiseksi on lukuisia ehdotuksia lähtien siitä, että koko kysymyksen asettelu on virheellinen, [23] toisessa päässä uskomus kvanttimekaniikan yleispätevyyteen objektiivisen fysikaalisen todellisuuden kuvaamiseksi.

Tarkkojen suureiden tapauksessa ehto (PR) on yhtäpitävä edellä muotoillun näennäisesti heikomman välittömään vertailuun liittyvän kalibrointiehdon kanssa, joten siitä luopuminen merkitsisi oleellisesti koko mittausteoriasta luopumista. Jos lisäksi aitoja kvanttiobjekteja on olemassa, eli ehto (QS) on pätevä, niin mittausparadoksin purku kohdistuu ensisijaisesti ehtoihin (QM) ja (U) sekä kysymykseen mittaustuloksen objektivoinnista, sen välttämättömistä ehdoista (O1) ja (O2).

3. Kvanttimekaniikan tulkinnoista

Kvanttimekaniikan minimitulkinta ymmärretään useimmiten mittaustulostilastotulkintana ja siinä pitäytyminen on täysin mahdollista. Tulkinta perustuu todennäköisyyden suhteellisen frekvenssin raja-arvo -tulkinalle ja siinä todennäköisyyden tulkinta usein samaistetaan (tarpeettomasti tai virheellisesti) todennäköisyysväittämien tavanomaiseen testausmenetelmään. Toinen tilastollinen tulkinta on ns. naiivi joukkotulkinta.

Huomautus 1. Mittaustulostilastoa voidaan kerätä toistamalla sama koe (systeemin preparointi – mittaus – rekisteröinti) peräjälkeen monta kertaa tai suorittamalla vastaava koe systeemijoukolle, identtisille, samalla tavalla preparoitujen, toisistaan riippumattomien systeemien kokonaisuudelle. Esimerkiksi, heittämällä samaa (tai identtistä) noppaa monta kertaa perättäin, tai heittämällä samanaikaisesti suuri joukko identtisiä noppia. Onnistuneet tilastot edellyttävät että aika- ja paikkavaihtelut eivät vaikuta tuloksiin. Kvanttimekaniikan näkökulmasta on paikallaan myös korostaa, että ensin mainitussa tapauksessa käytetty systeemi ei eri toistokertoina välttämättä (käytännössä ei koskaan) ole sama objekti; riittää, että toisto suoritetaan yksittäisillä keskenään identtisillä systeemeillä, kuten elektroneilla, neutroneilla, fullereenimolekyyleillä, tai fotoneilla suoritetuissa kaksoisrakokokeissa.

Mittaustulostilastotulkinnassa kvanttimekaniikka ymmärretään ensisijaisesti vain mittaustuloksia koskevana teoriana joka sisältää menetelmät mittaustulosten mahdollisten jakaumien laskemiseksi. Tällaisessa pragmaattisessa katsantokannassa tulkintaongelmat voidaan yksinkertaisesti sivuuttaa joko liian haastavina tai eräänlaisina pseudo-ongelmina. Mittausteoria, ehtoineen (PR), (QS), (QM), (U), on tässä kuitenkin keskeinen sillä se antaa konkreettisia malleja $\mathsf{M}$ fysikaalisen suureen $\mathsf{E}$ ja sen mittaustulostilastojen $p^\mathsf{E}_\rho$ realisoimiseksi jakaumilla $p^\mathsf{Z}_{\sigma^f}$. Ehto (O1) on tällöin vain eräs mahdollinen mittauksen ominaisuus. On ehkä paikallaan todeta, että usein käytössä olevasta tulkinnan ohi menevästä realistisesta puhetavasta riippumatta tämä on juuri se kvanttimekaniikka, jota tosiasiassa yleisimmin käytetään, mahdollisesti täydennettynä (kiistanalaisella) projektiopostulaattina tunnetulla olettamuksella (ks. jakso 3.1 ja myös Huomautus 3).

Naiivissa joukkotulkinnassa tyydytään tyypillisesti siihen, että kvanttimekaniikan aito todennäköisyysluonne on heijastumaa teorian väitetystä tai oletetusta epätäydellisyydestä. Tässä $\neg{\rm (QS)}$ -tulkinnassa kvanttimekaniikan tila ei kuvaa yksittäistä systeemiä vaan käsitteellistä ääretöntä identtisten ja keskenään vuorovaikutuksettomien systeemien joukkoa ja teorian tuottamat todennäköisyydet kuvaavat fysikaalisten suureiden arvojen jakautumisia joukon jäsenten kesken kyseisessä tilassa. Tällaisessa katsannossa teorian mahdolliset tulkintakysymykset sivuutetaan lähinnä triviaalilla tavalla. [24]

Luokkaan $\neg\rm(QS)$ kuuluvia kvanttimekaniikan (epätriviaaleja) tulkintoja ovat ns piilomuuttuja- tai kausaalitulkinnat, tulkinnat jotka pyrkivät täydentämään fysikaalisen systeemin kvanttimekaniikan mukaista tilakuvausta $\rho$ jollakin sopivalla muuttujalla $\lambda\in\Lambda$ niin, että ainakin joidenkin suureiden mittaustulostodennäköisyydet $p^\mathsf{E}_\rho(X)$ palautuisivat 0-1-arvoisiksi todennäköisyyksiksi $p^\mathsf{E}_{(\rho,\lambda)}(X)$. Koska kvanttimekaniikan todennäköisyysennusteilla on vankka kokeellinen tuki, niin tyypillisenä vaatimuksena on, että näiden ’havaintojen ulottumattomissa olevien’ parametrien $\lambda$ sopivalla keskiarvoistuksella saadaan kvanttimekaniikan todennäköisyydet; muodollisesti $p^\mathsf{E}_\rho(X)=\int p^\mathsf{E}_{(\rho,\lambda)}\,d\mu(\lambda)$, missä $\mu$ on sopiva piilomuuttuja-avaruuden todennäköisyysmitta. Tällaisten mallien kehittely juontuu Louis de Broglien (1926) ja David Bohmin (1952) töihin. Realistisina teorioina ne ovat välttämättä kontekstuaalisia [25] ja epälokaalisia, vert. K2.4.2. Pitäydymme tässä kirjoituksessa olettamuksessa (QS), joten emme paneudu tässä näihin tulkintoihin. [26]

Kvanttimekaniikan varsinaisten tulkintakysymysten lähtökohtana on yksinkertainen peruskysymys: voidaanko minimitulkintaa täydentää niin, että teorian puitteissa voitaisiin puhua yksittäisistä fysikaalisista systeemeistä (QS) ja niiden niiden ominaisuuksista niin että säästyttäisiin ristiriidalta (2.4). Kysymys on erityisen akuutti sillä yksittäisillä kvanttiobjekteilla tehtävät kokeet ovat olleet jo kauan arkipäivää ja kvanttiteknologia tuottaa yhä enemmän laitteita, jotka hyödyntävät yksittäisiä atomeja, elektroneja, ja fotoneja, ja niiden ominaisuuksia.

Kvanttimekaniikan tulkintojen moninaisuus on tavattoman laaja. Google Scholar tuottaa 0.17 sekunnissa 1 490 000 viittausta hakusanalla interpretation of quantum mechanics (poimittu 28.11.2023) joten kokonaiskuvan hahmottaminen tältä pohjalta on ylivoimainen tehtävä. Rajoittuminen uusimpiin tulkintaehdotuksiin ei myöskään helpota tehtävää kovin paljon, esimerkiksi hakusanat relational quantum mechanics, quantum bayesianism/qbism, ja quantum darwinism saavat vastaaviksi tunnusluvuiksi luvut 49 000, 20 600, ja 36 700. Niinpä seuraava katsaus on välttämättä varsin pelkistetty ja heijastaa kirjoittajan omaa tutkimushistoriaa ja omia mieltymyksiä.

Kvanttimekaniikan ensimmäinen tulkintahahmotelma jossa pyrkimyksenä oli juuri ymmärtää teoria yksittäisten atomiobjektien perusteoriana tunnetaan Kööpenhaminan tulkintana sen pääarkkitehdin Niels Bohrin koti-instituutin mukaan. [27] Aloitamme tämän tulkinnan lyhyellä katsauksella. On kuitenkin todettava, että muuna kuin historiallisena ilmiönä, termi Kööpenhaminan tulkinta on kokenut lähes täydellisen inflaation. Näin siksi, että valtaosa teorian ja sen tulkinnan myöhemmästä hyvinkin eri suuntiin menevästä kehitystyöstä on ammentanut motivaationsa teorian uranuurtajien ajatuksista ja identifioi itsensä näin Kööpenhaminan tulkinnan laajan sateenvarjon alle. [28]

3.1. Kööpenhaminan tulkinta, projektiopostulaatti. Kööpenhaminan tulkinta rakentui Bornin ehdottamalle teorian todennäköisyystulkinnalle ja se muotoutui keskeisiltä osiltaan vuonna 1927 Niels Bohrin, Werner Heisenbergin, ja Wolfgang Paulin välisissä keskusteluissa, [29] täsmentyen John von Neumannin ja Paulin systemaattisissa teoksissa Mathematische Grundlagen der Quantenmechanik (1932) ja Die allgemeinen Prinzipien der Wellenmechanik (1933). Vaikka Bornin todennäköisyystulkinta, Bohrin komplementaarisuusnäkökulma, Heisenbergin epätarkkuusrelaatiot sekä von Neumannin projektiopostulaatti ovat tulkinnan keskeisiä piirteitä, niin on huomattava, että ei ole olemassa mitään yhtenäistä ja johdonmukaista Kööpenhaminan tulkintaa ellei siksi haluta nostaa projektiopostulaatilla täydennettyä minimitulkintaa.

3.1.1. Bohr ja Heisenberg. Bohrin ja Heisenbergin töiden lähtökohdan muodosti paradoksi, jonka Carl Friedrich von Weizsäcker on kiteyttänyt muotoon: kvanttiteoria syrjäyttää klassisen fysiikan, kvanttiteoria todennetaan kokeilla, kokeiden kuvaaminen edellyttää klassista fysiikkaa. [30]

Bohrille tämä dilemma näyttäytyi siinä, että tietyt klassiset käsiteparit tai kuvaustavat jotka ovat välttämättömiä atomi-ilmiöiden kokonaisvaltaiseksi ymmärtämiseksi ovat aalto-hiukkas dualismin takia toisensa poissulkevia. Tämän kuvaamiseksi Bohr otti käyttöön termin komplementaarisuus ja kehitteli siihen liittyviä ajatuksiaan kuuluisassa Comon luennossaan 1927 (alaviite 29), ja laajensi ja työsti niitä lukuisissa kirjoituksissaan seuraavien 35 vuoden aikana eräänlaiseksi filosofiseksi näkökulmaksi. [31] Bohr ei kuitenkaan koskaan tarkemmin määritellyt komplementaarisuuskäsitettään, mutta kuvaili sitä monitahoisesti tiettyjen kuvaustapojen välisenä suhteena, esimerkiksi avaruus-aika -kuvaus vs. kausaalikuvaus, fysikaalisten käsitteiden välisenä suhteena, esimerkiksi paikka vs. liikemäärä, kuvien välisenä suhteena, esimerkiksi hiukkaskuva vs. aaltokuva, sekä toisensa poissulkevia koejärjestelyjä edellyttävien ilmiöiden välisenä suhteena. Hän kuitenkin katsoi, että kvanttimekaniikan formalismi on pätevä komplementaaristen kuvaustapojen työkalu, joka myös selkeytti kvanttiteorian havainto-ongelmaa. Bohrin omin sanoin: [32]

A clarification of the situation as regards the observation problem in quantum theory . . . was first achieved after the establishment of a rational quantum mechanical formalism. . . . In the first place, we must recognise that a measurement can mean nothing else than the unambiguous comparison of some property of the object under investigation with a corresponding property of another system, serving as a measuring instrument, and for which this property is directly determinable according to its definition in everyday language or in the terminology of classical physics.

Heisenberg hyväksyi saman ristiriidan lähtökohdakseen (ks. alaviite 30) mutta pyrki löytämään sille positiivisen ratkaisun tarkastelemalla fysikaalisten suureiden määrittelyn ja mittaamisen mahdollisuuksia, omaksuen kannan jonka mukaan käytössä oleva teoria määrää mitä kulloinkin voidaan havaita. Heisenbergin johtopäätös oli, että kaikki ne käsitteet, kuten paikka, nopeus, rata, ja energia, joita tarvitsemme fysikaalisen systeemin klassisen mekaniikan mukaisessa kuvauksessa voidaan määritellä tarkasti myös atomaarisille prosesseille, siis kvanttimekaniikassa. Mutta koejärjestelyt jotka mahdollistavat tällaiset määrittelyt sisältävät väistämätöntä epätarkkuutta, kun niitä sovelletaan kahden kanonisesti konjugoidun suureen, kuten paikka ja liikemäärä, samanaikaiseen määrittämiseen. Tämän epätarkkuuden kvantifioimiseksi hän muotoili kuuluisat epätarkkuusrelaationsa $\delta q\cdot\delta p\sim h$ joiden hän katsoi antavan myös intuitiivisen selityksen aiemmin yhdessä Max Bornin ja Pascual Jordanin kanssa johdetuille ’vaihtorelaatioille’ $QP-PQ= i h/2\pi $. Pyrkimyksistään huolimatta Heisenbergin tarkastelut jäivät hyvin heuristiselle ja intuitiiviselle tasolle eikä niissä juuri lainkaan hyödynnetty teorian matemaattista rakennetta.

Keskeinen osa Bohrin ja Heisenbergin intuitiivisista ajatuksista on saanut täsmällisen muotoilun kvanttimekaniikan perusteoriassa, osin jo von Neumannin teoksessa. Teorian todennäköisyystulkinta eliminoi aalto-hiukkas -dualismin kvanttimekaniikan käsitteistöstä. [33] Toisensa poissulkevat kuvaukset, suureet, ja koejärjestelyt puolestaan ilmenevät monin eri tavoin teorian epäkommutatiivisuusrakenteissa, esimerkiksi tiettyjen suureparien todennäköisyysennusteissa (esimerkiksi, jos toisen suureen jakauma annetussa tilassa on vahvasti keskittynyt, niin toisen on välttämättä hyvin hajautunut samassa tilassa), tällaisten suureparien yhteismittausten puuttumisena (ks. esim. K1.6) tai niiden mittausten toisilleen aiheuttamissa ’häiriöissä’ (ks. esim. K1.7). Yksittäisen fysikaalisen suureen määrittely ja mittaus kvanttimekaniikan puitteissa voidaan toteuttaa tarkasti ja täysin analogisesti klassisen teorian kanssa, esimerkiksi avaruus-ajan symmetrioita käyttäen. Lisäksi Heisenbergin ajatus kanonisesti konjugoitujen suureparien, kuten paikka ja liikemäärä, samanaikaisesta epätarkasta mittaamisesta on voitu osoittaa oikeaan osuneeksi sen jälkeen kun von Neumannin teoriaa oli laajennettu vastaamaan paremmin realistisia mittaustilanteita (ks. K1.8).

Sekä komplementaarisuus että epätarkkuus toimivat kvanttimekaniikan alkuvuosina ikään kuin liikennemerkkeinä ilmaisemaan miten klassisia käsitteitä voidaan ristiriidattomasti käyttää atomaarisista ilmiöistä puhuttaessa. Tällaista ’kielioppia’ ei enää tarvita kun näihin käsitteisiin liittyvät näkökulmat on identifioitu johdonmukaisen teorian luonnollisina rakenteina.

Kysymys klassisen kielen mahdollisesta välttämättömyydestä mittaustulosten objektivoinnissa on kuitenkin asia erikseen. Tämä kysymys nousi selvästi esille ja myös tarkentui von Neumannin kehittämässä mittausprosessin kvanttimekaniikan mukaisessa kuvauksessa, joka muodostaa nykyisen, edellä hahmotellun, mittausteorian lähtökohdan.

Huomautus 2. Bohrin ja Heisenbergin töiden lähtökohtana oleva paradoksi on itsessään ongelmallinen. On selvää, että kvanttiteoria syrjäyttää klassisen fysiikan ainakin atomaarisella tasolla mutta vähemmän selvää on, että esimerkiksi planeettojen liikkeiden analyysissa näin olisi asianlaita. Kuitenkin, jos kaikki aine on kokoonpantu kvanttimekaniikan kuvauksen mukaisista mikroskooppisista osistaan, niin kvanttimekaniikan yleispätevyydelle on myös vaikea asettaa rajaa. von Weizsäckerin muotoileman paradoksin toinen lause ”kvanttimekaniikka todennetaan kokeilla” lienee kiistaton. Sen sijaan sen kolmas osa ”kokeiden kuvaaminen edellyttää klassista fysiikkaa” on taas kiistanalainen. Geologis-evolutionaarisessa aikaskaalassa mitättömän lyhyessä kirjoitetun historian ajanjaksossa esimerkiksi luonnon kuvaamiseen käytetty käsitteistö on kehittynyt melkoisin harppauksin vaikkapa vain aristoteelisesta galilei-newtonilaiseen ja siitä einsteinilaiseen kieleen. Olisi outoa jos käsitteiden kehittyminen olisi pysähtynyt tuohon klassisen fysiikan vaiheeseen: ”uusien käsitteiden löytäminen ja nimeäminen vaatii luovaa ajattelua, näin kohtaamme uudet ilmiöt” (Joel Haahtela, Helsingin Sanomat, s.6, 11.2.2024). Jos kielitieteilijä Noam Chomskyä on uskominen niin ihmisen kieli ja sen kehitys ei ole rajautunut puhuttuun, saatikka kirjoitettuun kieleen, vaan on oleellisesti ihmisen molekyylirakenteisiin koodatussa perimässä, ja kvanttimekaniikka on ihmisen kirjoittamaa kieltä, jolla juuri tällaisia rakenteita ymmärretään.

3.1.2. von Neumann. von Neumannin mukaan mittaustapahtuma voidaan analysoida hyvinkin yksityiskohtaisesti kvanttimekaniikan puitteissa, eli erityisesti ehto (QM) on voimassa, mutta viime kädessä mittaus aina päättyy siihen että havaitsija, jota teoria ei von Neumannin mukaan kuvaa, tulee tietoiseksi mittaustuloksesta: ehto (QM) on välttämätön muttei riittävä mittaustapahtuman loppuunsaattamiseksi. Koska rajaa teorian kuvaaman mittausprosessin ja teorian ulkopuolisen havaitsijan välillä voidaan siirtää analysoimalla prosessia yhä pidemmälle niin von Neumann näki tämän asettavan hahmottelemalleen mittausteorialle konsistenssivaatimuksen: tulos ei saa riippua siitä mihin raja vedetään; von Neumannin kuvaannollista esimerkkiä käyttäen prosessia voidaan jatkaa kunnes mittausjonon viimeiseltä asteikolta heijastunut valokvantti iskeytyy havaitsijan silmän verkkokalvolle rekisteröiden tuloksen havaitsijan tietoisuuteen. Todennäköisyyden reprodusointiehdolle rakentuva kvanttimekaniikan mittausteoria toteuttaa määritelmänsä mukaan automaattisesti tämän konsistenssivaatimuksen.

von Neumannin mukaan mittausongelmaa ei synny koska mittaus päättyy aina siihen, että teorian ulkopuolinen havaitsija tiedostaa mittaustuloksen, asteikkosuureen tosiasiallisen arvon. Kun havaitsija on tiedostanut tämän tuloksen, niin von Neumannin mukaan systeemin $\mathcal{S}$ mittauksen jälkeinen tila $\rho^f$, joka on muotoa (2.2), romahtaa (tai päivittyy) tiedostettua mittaustulosta vastaavaan komponenttitilaan, siis joko tilaksi $\hat m_+(\rho)$ tai tilaksi $\hat m_-(\rho)$. Jos mittaus on (kuten von Neumannin mallissa) toistava niin tällöin myös suureella $\mathsf{E}$ on (probabilistisella varmuudella) vastaava arvo, ja jos mittaus on lisäksi ihanteellinen niin tämä tila on joko $p^\mathsf{E}_\rho(\{+\})^{-1}E_+\rho E_+$ tai $p^\mathsf{E}_\rho(\{-\})^{-1}E_-\rho E_-$. Tilan romahtamista kuvaava olettamusta kutsutaan usein projektiopostulaatiksi.[34]

Bohr, Heisenberg, ja varsinkin Pauli, hyväksyivät von Neumannin mittausprosessin analyysin mutta katsoivat, että mittausprosessi päättyy tuloksen rekisteröintiin mittalaitteen klassiseen osaan, eli että ehto (QM) ei ole yleispätevä. He hyväksyivät myös projektiopostulaatin eli olettamuksen, että mitattavan systeemin tila romahtaa tuloksen rekisteröityessä mittaustulosta vastaavaksi ominaistilaksi, joko tilaksi $p^\mathsf{E}_\rho(\{+\})^{-1}E_+\rho E_+$ tai $p^\mathsf{E}_\rho(\{-\})^{-1}E_-\rho E_-$.

Huomautus 3. Koska tilan merkitys on sen tuottamissa mittaustulostodennäköisyyksissä, niin huomaamme, että projektiopostulaatti on siinä mielessä redundantti, että ehdolliset todennäköisyydet $p^\mathsf{F}_{\hat m_\pm(\rho)}(Y)$ palautuvat jono- ja kaksoistodennäköisyyksiin (ks myös alaviite 17): $$ p^\mathsf{Z}_{\sigma^f}(\{\pm\})p^\mathsf{F}_{\hat m_\pm(\rho)}(Y)=p^{\mathsf{F} \otimes \mathsf{Z}}_{V(\rho\otimes\sigma)}(Y\times\{\pm\}). $$ Todennäköisyyksien $p^\mathsf{Z}_{\sigma^f}(\{\pm\})$ ja $p^{\mathsf{F} \otimes \mathsf{Z}}_{V(\rho\otimes\sigma)}(Y\times\{\pm\})$ testaaminen ei riipu mitenkään siitä romahtiko systeemin $\mathcal{S}$ tila vai ei. Projektiopostulaatti on lähinnä realistista puhetapaa tukeva metafora. Lisäksi projektiopostulaatti esitetään usein niin, että tila romahtaa mitattavan suureen mittaustulosta vastaavaksi ominaistilaksi, siis (kaksiarvoisen suureen tapauksessa) muodossa $\rho\mapsto p^\mathsf{E}_\rho(\{\pm\})^{-1}E_\pm\rho E_\pm$. Tässä muotoilussa teorian tulkinta asettaa voimakkaita rajoituksia teorian kuvaamille mittauksille: vain ihanteelliset toistavat mittaukset ovat mittauksia.

Kvanttimekaniikan Kööpenhaminan tulkinnan keskeiset piirteet ovat luonnollinen osa kvanttimekaniikan matemaattis-käsitteellistä perustaa. Sen sijaan vetoaminen klassiseen fysikkaan tai teorian ulkopuoliseen tiedostavaan havaitsijaan kvanttimekaniikan mittausongelman ratkaisuna ei ole saanut yleistä hyväksyntää osakseen. Vetoaminen klassiseen fysiikkaan synnyttää vaikean kysymyksen kvanttimekaniikan ja klassisen mekaniikan pätevyysalueista sekä kysymyksen kvanttimekaniikan mahdollisesta klassisesta rajasta. Samaten teorian tavoittamattomaan tietoisuuteen vetoaminen on epätyydyttävää. Lisäksi projektiopostulaatin ad hoc -luonne on ongelmallinen tuoden stokastisen tilamuunnoksen systeemin luonnollisen kausaalin, jatkuvan, kääntyvän evoluution rinnalle.

Huomautus 4. Fritz London ja Edmond Bauer (1939) kehittelivät von Neumannin mittaus- ja havannointitapahtuman analyysia askeleen pidemmälle sisällyttämällä tiedostavan havaitsijan kvanttimekaniikan kuvaukseen antamalla mittalaitteelle, havaitsijalle, kyvyn tulla tietoiseksi mittauksen jälkeisestä tilastaan: ”olen tilassa $\sigma^f_k$”, missä $k$ on joko $+$ tai $-$, ”joten mitattava systeemi on vastintilassaan $\hat m_k$, ja suureella $\mathsf{E}$ on siksi arvo $k$”. He eivät kuitenkaan kuvanneet millään tavalla tätä havaitsijalle/mittalaitteelle antamaansa kykyä. Vastaavia tulkintaehdotuksia on esitetty aikojen saatossa useita, esimerkkinä Simon Kochenin 1985 kehittelemä kvanttimekaniikan ns. silminnäkijätulkinta, witnessing interpretation, jossa keskenään vuorovaikuttavat systeemit $\mathcal{S}$ ja $\mathcal{M}$ todistavat toinen toisensa tilat ja siis ominaisuudet. [35] Myös Kochen jättää avoimeksi sen miten todistamiskyky (valinta mahdollisten komponenttitilojen kesken) tosiasiassa toimii. Stuart Hameroff ja Roger Penrose ovat katsauskirjoituksessaan ”Consciousness in the universe: A review of the ‘Orch OR’ theory” (2014) ottaneet seuraavan askeleen tarkastelemalla tapahtumien tiedostamista eräänlaisena mikrotubulien mahdollistaman aivoissa tapahtuvan kvanttilaskennan päätepisteenä ja perustellen tältä pohjalta kvanttitilan ns. ”orkesteroidun objektiivisen reduktion” mallia. Aivojen toimintaa ei kuitenkaan tunneta vielä likimainkaan niin, että tätä Orch OR mallia voitaisiin pitää tieteellisesti perusteltuna mallina. Jos näkökulma kuitenkin osoittautuisi mahdolliseksi niin tässä kuvattu ”objektiivinen reduktio” on joka tapauksessa havaitsijakohtainen ja siinä mielessä vahvasti subjektiivinen. Olisiko mahdollista, että kahden eri havaitsijan kokemat ”objektiiviset reduktiot” samasta tapahtumasarjasta, suureen $\mathsf{E}$ mittaamisesta ja tuloksen tiedostamisesta, olisivat eriävät? Kysymys voidaan helposti analysoida kvanttimekaniikan mittausteorian puitteissa ja vastaus riippuu siitä minkälaiset suureen $\mathsf{E}$ mittaukset havaitsijat $\mathcal{M}_1$ ja $\mathcal{M}_2$ suorittavat: jos he molemmat suorittavat joko samanaikaisesti, tai jonossa kummassa tahansa järjestyksessä, saman (tilamuunnoksen synnyttävän) toistavan mittauksen niin tulokset ovat välttämättä samat. Saavutettu ”intersubjektiivisuus” riippuu kuitenkin mittausten ominaisuuksista eikä siis ole yleisesti pätevä.

3.2. Rinnakkaiset ja mahdolliset maailmat. Rinnakkaisten maailmojen tulkinta tai monimaailmatulkinta hyväksyy kvanttimekniikan yleispätevyyden mutta kiistää mittaustuloksen objektivointiongelman toteamalla ettei mittauksessa tapahdu mitään tuloksen objektivointia vaan että kaikki mittausvuorovaikutuksen tuottamat mahdollisuudet toteutuvat erillisissä rinnakkaisissa todellisuuksissa. Kvanttimekaniikan modaalitulkinnat puolestaan tyytyvät yhteen maailmaa mutta pyrkivät lieventäämään varmaan ennustettavuuteen liittyvää todellisuusehtoa. Kumpikin tulkintakategoria on itsessään hyvin monitahoinen ja laaja joten tyydyn tässä hahmottelemaan vain niiden yleispiirteitä.

3.2.1. Monimaailmatulkinnat. Monimaailmatulkintojen lähtökohtana on Hugh Everettin työ “The ‘Relative State’ Formulation of Quantum Mechanics,” vuodelta 1957. Tulkinta tuli laajempaan tietoisuuteen Bryce DeWittin ja Neill Grahamin kirjan The Many-Worlds Interpretation of Quantum Mechanics ilmestyttyä 1973, joka myös nimesi tulkinnan monimaailmatulkinnaksi. [36] Kirjan johdannosta saa lukea:

In 1957, in his Princeton doctoral dissertation, Hugh Everett, III, proposed a new interpretation of quantum mechanics that denies the existence of a separate classical realm and asserts that it makes sense to talk about a state vector for the whole universe. This state vector never collapses, and hence reality as a whole is rigorously deterministic. This reality, which is described jointly by the dynamical variables and the state vector, is not the reality we customarily think of, but is a reality composed of many worlds. By virtue of the temporal development of the dynamical variables the state vector decomposes naturally into orthogonal vectors, reflecting a continual splitting of the universe into a multitude of mutually unobservable but equally real worlds, in each of which every good measurement has yielded a definite result and in most of which the familiar statistical quantum laws hold.

Tästä tieteisfiktion kaltaisesta johdantokatkelmasta huolimatta tulkinnan lähtökohtana on ajatus, että koko maailmankaikkeudesta voidaan ottaa erilliseen tarkasteluun muusta maailmasta eristetettävissä oleva fysikaalinen systeemi $\mathcal{S}$ jonka mahdollisista ominaisuuksista, suureiden arvoista, teorian kuvaama havaitsija $\mathcal{M}$ saa tietoa perinteisin (yllä kuvatun) mittausteorian keinoin. Havaitsijalla on kyky rekisteröidä havaitsemansa tulos, jota kykyä ei kuitenkaan erikseen eritellä. [37]

Havainnointiaan varten havaitsija $\mathcal{M}$, joka on puhtaassa valmiustilassa $\sigma$, kytkeytyy (unitaarisella) vuorovaikutuksella $V$ systeemiin $\mathcal{S}$, joka on puhtaassa alkutilassa $\rho$. Matemaattisteknisesti tila $V(\rho\otimes\sigma)$ määrittelee, kuten edellä, yksikäsitteiset (sekoitetut) alisysteemitilat $\rho^f$ ja $\sigma^f$ mutta niillä ei nyt tässä ole keskeistä asemaa. Sensijaan tämän kietoutuneen ’universaalin puhtaan tilan’ $V(\rho\otimes\sigma)$ avulla havaitsija $\mathcal{M}$ määrittelee systeemin $\mathcal{S}$ puhtaan tilan omaan puhtaaseen tilaansa nähden, jonka hän identifioi (rekisteröi) tilasta $V(\rho\otimes\sigma)$. Tätä varten havaitsija on kiinnittänyt oman tarkasteluperspektiivinsä, ns. (puhtaat) asteikkotilat. Havaitakseen (tarkan) suureen $\mathsf{E}$ havaitsija $\mathcal{M}$ on säätänyt perspektiivinsä niin, että prosessi on toistava ja tuottaa vahvat korrelaatiot, jolloin kaksiarvoisen suureen $\mathsf{E}$ tapauksessa tilan $V(\rho\otimes\sigma)$ sekoitetuille tiloille $\rho^f$ ja $\sigma^f$ saadaan hajotelmat (2.1) ja (2.2):

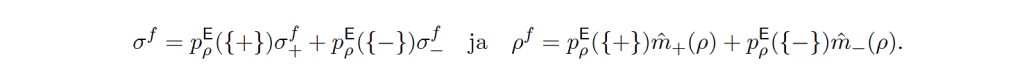
Vaikka näillä hajotelmilla ei nyt ole mitään itsenäistä merkitystä, niin niissä näkyvät vahvasti korreloidut puhtaat tilaparit $(\sigma_+^f, \hat m_+(\rho))$ ja $(\sigma_-^f, \hat m_-(\rho))$ muodostuvat havainnoitsijan asteikkotiloista sekä havaittavan suureen ominaistiloista, lisäksi havaintoasetelma (mittaus) on valittu niin, että tila $V(\rho\otimes\sigma)$ on puhtaiden tilojen $\sigma_+^f\otimes\hat m_+(\rho)$ ja $\sigma_-^f\otimes\hat m_-(\rho)$ superpositio. Everettin mukaan mitään tilan $V(\rho\otimes\sigma)$ romahdusta ei tapahdu vaan sen sisältämät molemmat mahdollisuudet (suhteessa kiinnitettyyn perspektiiviin) toteutuvat erillisissä maailmoissa (tilat ovat ’ortogonaaliset’); mittaus on jakanut havaitsijan maailman (ja ehkä myös havaitsijan) kahteen riippumattomaan rinnakkaiseen yhtä todelliseen osaan joista toisessa hän on rekisteröinyt tuloksen ’kyllä’, systeemi $(\mathcal{S}, \mathcal{M})$ tilassa $\hat m_+(\rho)\otimes\sigma^f_+$, toisessa tuloksen ’ei’, systeemi $(\mathcal{S}, \mathcal{M})$ tilassa $\hat m_-(\rho)\otimes\sigma^f_-$. Everettin [38] mukaan tilan $V(\rho\otimes\sigma)$ sisältämät vahvat korrelaatiot tilojen $\sigma^f_+$ ja $\hat m_+(\rho)$ sekä $\sigma^f_-$ ja $\hat m_-(\rho)$ välillä ovat juuri osoitus siitä että (hyvä) mittaus on suoritettu: mittaus on havaitsijan vahvaa korreloitumista havaintokohteensa kanssa.

Huomautus 5. Vaikka $p^\mathsf{E}_\rho$ on aina (kaikilla $\mathsf{E}$ ja $\rho$) hyvin määritelty todennäköisyysmitta, niin sen merkitystä ei voida antaa aiemmin kuvatulla kokeen toistolle perustuvan mittaustulostilaston avulla. Tästä huolimatta todennäköisyyksille, kuten $p^\mathsf{E}_\rho(\{\pm\})$, saadaan suhteellisen frekvenssin raja-arvo -tulkinta kun havaitsija $\mathcal{M}$ suorittaa kyseisen suureen $n$-kertaisen mittauksen samalla tavalla valmistettujen keskenään identtisten systeemien $\mathcal{S}_i=\mathcal{S}$ systeemijoukolle $\mathcal{S}^{(n)}=(\mathcal{S}_1, \ldots, \mathcal{S}_n)$ rekisteröiden havaitsemansa tulosjonon $\ell=(\ell_1,\ldots\ell_n), \ell_k\in\{+,-\}$, ja tallentaen sen muistiinsa. Jos $f^{(n)}_+(\ell)$, vast. $f^{(n)}_- (\ell)$ on tuloksen $+$, vast. $-$, suhteellinen lukuisuus muistijonossa $\ell$, niin voidaan osoittaa, että luku $f^{(n)}_\pm(\ell)$ lähestyy lukua $p^\mathsf{E}_\rho(\{\pm\})$ kun $n\to\infty$ melkein kaikilla jonoilla $\ell=(\ell_1,\ldots\ell_n)$. [39]

Huolimatta oudosta intuition vastaisesta todellisuuskuvastaan Everettin työlle rakentuva kvanttimekaniikan monimaailmatulkinta, sen eri muunnelmin, on mitä ilmeisimmin johdonmukainen tulkinta joka välttää kvanttimekaniikan mittausongelman. Tulkinalla on vankat kannattajansa mutta myös vastustajansa ja keskustelu sen asemasta ja merkityksestä on edelleen varsin vilkasta. [40] Tämän tulkinnan eräissä (kosmologisissa) versioissa ajatellaan, että kvanttimekaniikan tila on universaali, kuvaten koko maailmankaikkeutta. Tällaista tilaa ei luonnollisestikaan voida preparoida vaan systeemi, koko universumi, on jossakin tilassa joka luonnollisella tavalla kehittyy ajan myötä kausaalisti, jatkuvasti, ja kääntyvästi, josta kuitenkin voidaan saada osittaista tietoa tässä maailmankaikkeuden pikku kolkassa nimeltä Maa. Tässä irtaudutaan fysiikan perinteisistä metodologisista periaatteista ja ollaan tämän kirjoittajan käsityksen mukaan melko harmaalla alueella.

3.2.2. Modaalitulkinnat. Kvanttimekaniikan modaalitulkinnat pyrkivät kehittämään teorian sallimissa puitteissa realistista puhetapaa fysikaalisen suureen arvoista ajautumatta mittausongelmaan. Tulkinnat hyväksyvät varmaan ennustettavuuteen liittyvän puhetavan (vrt. jakso 2.1), mutta hylkäävät sen välttämättömyyden; ajatuksen, joka von Neumannin mittausprosessin analyysissa johti projektiopostulaattiin, tilan romahtamiseen mittaustulosta vastaavaksi ominaistilaksi. Epäobjektiivisen suureen tapauksessa tulkinnat määrittelevät riittäviä ehtoja suureen niille arvoille joita sillä voisi olla kyseisessä tilassa. Modaalitulkintoja on kehitelty erityisesti 1980- ja 90-luvuilla, ehkä tunnetuimpana Bas van Fraassenin teoksessaan Quantum Mechanics: an empiricist view (Clarendon, 1991) kehittämä modaalitulkinnan ”kööpenhaminalainen versio”, nimen viitatessa juuri siihen, että lähtökohtana on von Neumannin muotoilema kvanttimekaniikka, sen päivitetyssä versiossa, ilman projektiopostulaattia. Tarkastelemme esimerkkinä tämän tulkinnan keskeisiä muotoiluja tarkan kaksiarvoisen suureen mittauskontekstissa.

Olkoon $\mathsf{M}=(\mathcal{K},\mathsf{Z},\sigma,V)$ kaksiarvoisen tarkan suureen $\mathsf{E}$ mittaus ja $\rho$ systeemin $\mathcal{S}$ tila ennen mittausta. Kalibrointiehdon mukaan, jos suureella $\mathsf{E}$ on (probabilistisen varmuuden mielessä) jompi kumpi mahdollisista arvoistaan tässä tilassa, niin asteikkosuureella $\mathsf{Z}$ on vastaava arvo mittalaitteen mittauksen jälkeisessä tilassa $\sigma^f$. Jos taas $\mathsf{E}$ on epäobjektiivinen tässä tilassa, niin mittaus tuottaa (probabilistisella varmuudella) jomman kumman mahdollisista mittaustuloksista tilan antamalla todennäköisyydellä, sillä $p^\mathsf{E}_\rho(\{+\})+p^\mathsf{E}_\rho(\{-\})=1$. Modaalitulkinta lähtee siitä, että ehto ”mittaus tuottaa jomman kumman tuloksen” sisältää oletuksen, että asteikkosuureella on jompi kumpi näistä arvoista mittauksen jälkeen. Tulkinnan peruskysymys onkin objektivointiongelma välttäen määritellä ne ehdot, joilla asteikkosuureella, ja mahdollisesti myös mitatulla suureella, voisi olla jompi kumpi arvoista $\pm$ mittauksen jälkeisessä tilassa. Näiden ehtojen muotoileminen edellyttää taustalla olevien rakenteiden avaamista, josta lyhyesti alla.

Taustatietoa 1. Tarkastellaan geneeristä systeemiä $\mathcal{S}$ (joko mitattava systeemi tai mittalaite) ja sen tiloja $\rho\in \boldsymbol{S}(\mathcal{H})$. Olkoon $\boldsymbol{P}(\mathcal{H})$ kaikkien tarkkojen efektien (teknisesti projektioiden) joukko. Ilmaisun lyhentämiseksi käytämme tässä tarkoista efekteistä nimitystä ominaisuus. Jokaista tilaa $\rho$ kohti on olemassa (yksikäsitteinen) suppein, tai pienin, ominaisuus $P_\rho$, joka systeemillä $\mathcal{S}$ on varmuudella tässä tilassa, toisin sanoen, $tr{[\rho P_\rho]}=1$, ja jos $tr{[\rho R]}=1$ myös jollekin toiselle ominaisuudelle $R$, niin $tr{[\gamma P_\rho]}\leq tr{[\gamma R]}$ kaikilla tiloilla $\gamma$. Sanomme, että ominaisuus $P_\rho$ sisältyy ominaisuuteen $R$ ja merkitsemme $P_\rho\leq R$. Jos tila $\rho$ on puhdas, niin $P_\rho=\rho$, eikä ole olemassa mitään suppeampaa ominaisuutta joka voisi sisältyä ominaisuuteen $P_\rho$, ominaisuus on atomaarinen. Juuri tämän takia puhtaat tilat voidaan samastaa luetteloksi niistä ominaisuuksista, jotka systeemillä on varmuudella tässä tilassa. Jos tila $\rho$ ei ole puhdas, niin on olemassa ominaisuuksia $R$ jotka sisältyvät ominaisuuteen $P_\rho$ yllä kuvatussa (todennäköisyysteoreettisessa) mielessä, mutta voisiko systeemillä olla myös tällainen ominaisuus tilassa $\rho$?

Yllä esitettyyn kysymykseen vastaamiseksi tarkastellaan kahta tilaa $\rho_1$ ja $\rho_2$. Sanomme, että tila $\rho_1$ on mahdollinen suhteessa tilaan $\rho_2$, ja merkitsemme $\rho_1\prec\rho_2$, jos $P_{\rho_1} \leq P_{\rho_2}$. Jokaiselle tilalle $\rho$ voidaan nyt määritellä seuraavat ominaisuusjoukot:

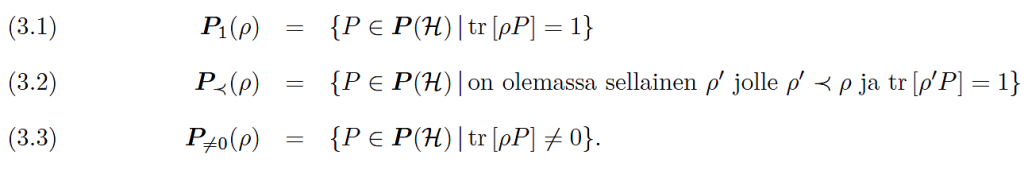
Selvästi, $\boldsymbol{P}_1(\rho)\subseteq \boldsymbol{P}_{\prec}(\rho)\subseteq \boldsymbol{P}_{\ne 0}(\rho)$, jossa ensimmäinen sisältymisrelaatio on yhtäsuuruus tarkalleen silloin kun tila $\rho$ on puhdas, $\rho^2=\rho$, ja jälkimmäinen kun $P_\rho=I$, identiteetti. Jos $\rho$ on sekoitettu tila, ja $\rho’$ sen mahdollinen puhdas komponentti, eli voidaan kirjoittaa $\rho=\lambda\rho’+(1-\lambda)\tilde\rho$, jollekin $0<\lambda\leq 1$ ja $\tilde\rho\in \boldsymbol{S}(\mathcal{H})$, niin $\rho’=P_{\rho’}\in \boldsymbol{P}_{\prec}(\rho)$. Itse asiassa, tämä joukko sisältää kaikki atomaariset ominaisuudet $P’$ jotka sisältyvät ominaisuuteen $P_\rho$.

Modaalitulkinnan kööpenhaminalaisen version mukaan yhtälön (3.2) joukko $\boldsymbol{P}_{\prec}(\rho)$ sisältää tarkalleen ne ominaisuudet, jotka systeemillä voi olla tilassa $\rho$ ja sillä on ne todennäköisyyksillä $tr{[\rho P]}\ne 0$. Jos tila $\rho$ on puhdas, niin tämä joukko sisältää tarkalleen ne ominaisuudet jotka systeemillä on varmuudella tässä tilassa.

Tarkastellaan nyt suureen $\mathsf{E}$ mittausta $\mathsf{M}$, ja olkoon systeemi $\mathcal{S}$ puhtaassa tilassa $\rho$. Systeemien $(\mathcal{S},\mathcal{M}), \mathcal{M}$ ja $\mathcal{S}$ (dynaamiset) tilat mittauksen jälkeen ovat $V(\rho\otimes\sigma), \sigma^f$, ja $\rho^f$, ja tilalle $\rho^f$ on aina voimassa hajotelma (2.1). Jos $\mathsf{E}$ on objektiivinen tilassa $\rho$, niin asteikkosuureella on (probabilistisella varmuudella) vastaava arvo. Tällöin $\sigma^f$ on jompi kumpi tiloista $\sigma^f_\pm$ (vrt. yhtälö (2.2)). Tästä ei kuitenkaan seuraa, että suureella $\mathsf{E}$ olisi tilassa $\rho^f$, joka on nyt jompi kumpi tiloista $\hat m_\pm(\rho)$, vastaava arvo. Jos $\mathsf{E}$ ei ole objektiivinen tilassa $\rho$, niin todennäköisyydet $p^\mathsf{Z}_{\sigma^f}(\{\pm\})=p^\mathsf{E}_\rho(\{\pm\})$ eroavat nollasta. Tästä ei kuitenkaan vielä seuraa, että asteikkosuureella voisi olla (modaalitulkinnan mielessä) tilassa $\sigma^f$ jompi kumpi arvoista $\pm$. Modaaliehto $\mathsf{Z}(\{\pm\})\in \boldsymbol{P}_{\prec}(\sigma^f)$ takaa tämän ja on samalla lisäehto mittaukselle. Sama koskee ehtoa $\mathsf{E}(\{\pm\})\in \boldsymbol{P}_{\prec}(\rho^f)$.

Muotoilemme vielä nämä modaalitulkinnan kööpenhaminalaisen version keskeiset olettamukset seuraavasti. Kaksiarvoisen tarkan suureen $\mathsf{E}$ mittauksessa $\mathsf{M}$ pätee:

(MC1) Jos $p^\mathsf{E}_\rho(\{i\})\ne 0, i\in\{+,-\}$, niin asteikkosuureella $\mathsf{Z}$ voi olla arvo $i$ mittauksen jälkeen, ts. $Z_i\in \boldsymbol{P}_{\prec}(\sigma^f)$, ja sillä on tämä arvo tilassa $\sigma^f$ todennäköisyydellä $p^\mathsf{E}_\rho(\{i\})$.

(MC2)] Jos $p^\mathsf{E}_\rho({i})\ne 0, i\in\{+,-\}$, niin suureella $\mathsf{E}$ voi mittauksen $\mathsf{M}$ jälkeen olla arvo $i$, ts. $E_i\in \boldsymbol{P}_{\prec}(\rho^f)$, ja sillä on tämä arvo tilassa $\rho^f$ todennäköisyydellä $p^\mathsf{E}_\rho(\{i\})$.

Kumpikin modaaliehto rajaa suureen $\mathsf{E}$ mahdollisten mittausten luokkaa. Voidaan helposti konsturoida esimerkkejä mittauksista jotka eivät toteuta näitä ehtoja. Toisaalta, jokainen vahvan korrelaation synnyttävä mittaus toteuttaa nämä ehdot. Lukuunottamatta ns. minimaalisia mittauksia, ehtojen (MC1) ja (MC2) tyhjentävä luokittelu on vielä tekemättä.

Modaalitulkinnat ovat pyrkimys luoda kvanttimekaniikalle kieli, tai puhetapa, jonka mukaan fysikaalisella suureella olisi jokin mahdollisista arvoistaan mittauksen jälkeen, ja siten ikään kuin ratkaista objektivointiongelma teorian sisäisin keinoin ilman ad hoc projektiopostulaattia ja pitäytymällä yhdessä maailmassa. Kuten monimaailmatulkinnat, ja myös monet muut realistista puhetapaa hahmottelevat tulkinnat, modaalitulkinnat rajoittavat mahdollisten mittausten luokkaa, sitä enemmän mitä suppeammaksi mittauksen jälkeisessä tilassa mahdollisten ominaisuuksien joukko rajataan. Joukon valintaan liittyvän mahdollisuuksien kirjon [41] lisäksi modaalitulkintojen ehkä kriittisin avoin kysymys on mittaustuloksen stabiilisuus: miten perustella asteikkosuureen arvon riittävä pysyvyys; ominaisuusjoukko $\boldsymbol{P}_{\prec}(\sigma^f)$, kuten myös $\boldsymbol{P}_{\prec}(\rho^f)$, muuntuu luonnollisella tavalla ajan myötä. [42]

3.3. Ympäristön vaikutus. Mittausongelman taustalla on oletus, että systeemi $\mathcal{S}$ ja mittalaite $\mathcal{M}$ on valmistettu ennen mittausta toisistaan ja ympäristöstä riippumattomasti puhtaisiin tiloihin $\rho$ ja $\sigma$ jolloin mittausvuorovaikutus $V$ muuntaa parin $(\mathcal{S}, \mathcal{M})$ alkutilan $\rho\otimes\sigma$ puhtaaksi kietoutuneeksi tilaksi $V(\rho\otimes\sigma)$, ja että pari $(\mathcal{S}, \mathcal{M})$ myös säilyy ympäristöstään eristettynä mittauksen jälkeen, ainakin niin kauan että pysyvä tulos on saavutettu. Ympäristön vaikutusta on kuitenkin vaikeaa kokonaan välttää ja se on sitä vaikeampaa mitä monimutkaisempi kvanttiobjekti, systeemi tai mittalaite, on ja mitä kauemmin prosessi kestää.

Ympäristön vaikutus mittaustapahtumaan, erityisesti mittauskytkennän lakattua, voidaan yrittää huomioida kahdella eri tavalla, olettamalla, että myös ympäristö $\Large{𝜀}$ voidaan kuvata kvanttimekaanisesti ja laajentamalla parin $(\mathcal{S}, \mathcal{M})$ mittausvuorovaikutuksen jälkeistä kuvausta kolmikon $(\mathcal{S}, \mathcal{M}, \Large{𝜀})$ kuvaukseksi, tai luopumalla yrityksestä kuvata ympäristö kvanttimekaanisesti ja hyväksymällä, että pari $(\mathcal{S}, \mathcal{M})$ on vuorovaikutuksen lakattua avoin, ei eristetty, systeemi jolloin sen dynaaminen evoluutio ei enää voi olla unitaarista. [43] Ensimmäisen lähestymistavan ongelmana on ympäristön ja varsinkin sen alkutilan tarkka määrittäminen sekä ympäristön $\Large{𝜀}$ ja parin $(\mathcal{S}, \mathcal{M})$ keskinäisen vuorovaikutuksen spesifiointi. Toisen, ehkä realistisemman lähestymistavan ongelmana taas on sen jossain määrin välttämättä ad hoc -luonne dynaamisen (ei-unitaarisen) evoluution määrittelyssä. Mittausongelman (2.4) näkökulmasta nämä lähestymistavat katsovat että ehto (U) ei ole riittävä mittauksen koko dynamiikan kuvaamiseksi. Kumpaakin lähestymistapaa on tutkittu runsaasti viimeisen puolivuosisadan ajan myös kvanttimekaniikan tulkintaongelman näkökulmasta. Koska ensin mainittu lähestymistapa periaatteessa sisältää jälkimmäisen lähestymistavan niin tyydymme tässä esittelemään vain ensin mainitun ja senkin osalta joudumme tyytymään vain suppeaan katsaukseen.

3.3.1. Dekoherenssi ja kvanttidarwinismi. Oletetaan, että systeemi $\mathcal{S}$ ja mittalaite $\mathcal{M}$ on onnistuttu eristämään riittävän hyvin ympäristöstään niin, että suureen $\mathsf{E}$ hetkellinen mittaus $\mathsf{M}$ on voitu toteuttaa mutta mittauksen päätyttyä ympäristön (esimerkiksi lämpötila-) vaikutusta ei voida enää kokonaan välttää. Jos ympäristö $\Large{𝜀}$ on kuitenkin kvanttimekaniikan avulla kuvattavissa ja kolmikko $(\mathcal{S}, \mathcal{M}, \Large{𝜀})$ muusta maailmasta riippumaton, niin sen evoluutio on annettavissa unitaarisesti mittauskytkennän lakattua hetkellä $t=0$ muodossa $W_t(V(\rho\otimes\sigma)\otimes\gamma), t\geq 0$, missä $\gamma$ on ympäristön ”alkutila”, tila hetkellä $t=0$. Kuten aina eristetyille systeemeille, tilan $\gamma$ voidaan olettaa olevan puhdas, joten $W_t(V(\rho\otimes\sigma)\otimes\gamma)$ on puhdas kietoutunut tila. Esimerkkitilanteessamme $V(\rho\otimes\sigma)$ on tulospareihin $(+,+)$ ja $(-,-)$ liittyvien puhtaiden tilojen $\hat m_+(\rho)\otimes\sigma^f_+$ ja $\hat m_-(\rho)\otimes\sigma^f_-$ superpositio. Niinpä myös $V(\rho\otimes\sigma)\otimes\gamma$ on (systeemien yhdistämissäntöjen nojalla, K2.1) puhtaiden tilojen $\hat m_+(\rho)\otimes\sigma^f_+\otimes\gamma$ ja $\hat m_-(\rho)\otimes\sigma^f_-\otimes\gamma$ superpositio. Koska superpositiorakenne säilyy unitaarisessa evoluutiossa $W_t$, niin on epävarmaa onko tästä lähestymistavasta odotettavissa mittausongelmalle mitään uutta ratkaisua.

Kolmikon $(\mathcal{S},\mathcal{M},\Large{𝜀})$ tila $W_t(V(\rho\otimes\sigma)\otimes\gamma)$ määrää kuitenkin minä tahansa myöhempänä hetkenä $t>0$ erityisesti sekä systeemin $\mathcal{S}$ että parin $(\mathcal{S}, \mathcal{M})$ tilat, jotka lähtökohtaisesti riippuvat sekä evoluutiosta $W_t$ että ympäristön alkutilasta $\gamma$. Toisin kuin mittauksen $\mathsf{M}$ tapauksessa, ympäristö $\Large{𝜀}$ ei kuitenkaan ole vapaasti valittavissa emmekä myöskään voi aktiivisesti säätää kytkentää $W_t$, ympäristön alkutilaa $\gamma$, emmekä poimia ympäristöstä sopivaa referenssisuuretta niin, että esimerkiksi parin $(\mathcal{S}, \mathcal{M})$ tilalle hetkellä $t>0$ voitaisiin helposti perustella mittausongelman ratkaisun kannalta välttämätön rakenne

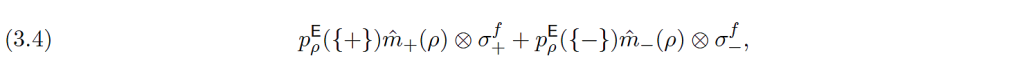
kuten edellä tiloille (2.1) ja (2.2). Vaikka tähän päästäisiinkin niin tulosparin $(+,+)$ tai $(-,-)$ mahdollinen rekisteröinti on edelleen kysymyksenalainen.

Riippumatta edellä mainituista ongelmista voidaan kuitenkin helposti konstruoida kytkentämalleja jossa esimerkiksi asteikkosuure kytkeytyy makroskooppisen ympäristön määrittelemään avaruudelliseen kontekstiin (paikkaan) niin, että parin $(\mathcal{S}, \mathcal{M})$ tilaksi hetkellä $t>t_d>0$ saadaan (likimain) muoto (3.4), missä $t_d$ on mallista riippuva kriittinen ’dekoherenssiaika’. Ilmiötä, jossa puhdas superpositiotila, kuten $V(\rho\otimes\sigma)$, muuntuu ulkoisesta vaikutuksesta sekoitetuksi tilaksi, kuten (3.4), kutsutaan dekoherenssiksi, superpositiotilan koherenssi ikään kuin ’tuhoutuu’. Tuhoutuminen on kuitenkin siinä mielessä näennäistä että, tilan $V(\rho\otimes\sigma)$ koherenssi (superpositiorakenne) on vain siirtynyt osaksi makroskooppista kvanttimekaanista ympäristöä, ollen tilassa $W_t(V(\rho\otimes\sigma)\otimes\gamma)$. Tämä näkyy mm. siinä että vaikka hajotelma (3.4) on parin $(\mathcal{S}, \mathcal{M})$ sekoitetun tilan (hetkellä $t>t_d$) luonnollinen (vuorovaikutusten tuottama) hajotelma, niin mikä tahansa kyseisen tilan hajotelma (joita on edelleen ääretön määrä) tuottaa tarkalleen samat todennäköisyysennusteet. [44] Dekoherenssin välttäminen, eli parin $(\mathcal{S}, \mathcal{M})$ pitäminen eristettynä, on kuitenkin vaikeaa ja se on teknisesti suuri haaste mm. kvanttitietokoneissa joissa laskennan etenemiseksi pitäisi pystyä ylläpitämään useiden (kymmenien, satojen, ehkä jopa tuhansien) kubittien superpositiotiloja.

Voisiko ympäristön aiheuttama dekoherenssi kuitenkin mahdollistaa mittausongelmalle käytännöllisen ratkaisun? Kuten edellä jo todettiin, tilaa (3.4)ei voida lähtökohtaisesti tulkita niin, että pari $(\mathcal{S}, \mathcal{M})$ olisi joko tilassa $\hat m_+(\rho)\otimes\sigma_+^f$ tai $\hat m_-(\rho)\otimes\sigma_-^f$, painokertoimien $ p^\mathsf{E}_\rho(\{+\})$ ja $p^\mathsf{E}_\rho(\{-\})$ ilmaistessa tietomme vajavaisuutta systeemiparin tosiasiallisesta tilasta. Tämä johtuu juuri parin $(\mathcal{S}, \mathcal{M})$ kietoutumisesta ympäristöön $\Large{𝜀}$, sekoitettu tila (3.4) määräytyy puhtaasta tilasta $W_t(V(\rho\otimes\sigma)\otimes\gamma)$. Kvanttidarwinismiksi [45] kutsutussa kvanttimekaniikan tulkintahahmotelmassa parin $(\mathcal{S}, \mathcal{M})$ tilan (3.4) ’objektiivisuutta’, sekä siihen liittyen tilan $V(\rho\otimes\sigma)$ mahdollista efektiivistä lysähdystä tilaksi $\hat m_i(\rho)\otimes\sigma_i^f$, $i\in\{+,-\}$, perustellaan parin $(\mathcal{S}, \mathcal{M})$ de facto ympäristöriippumattomuudella. Tämä tulos saadaan tarkastelemalla parin $(\mathcal{S}, \mathcal{M})$ tilaa hetkellä $t>t_d$ koko ympäristön $\Large{𝜀}$ sijasta sen mahdollisten riippumattomien osien $\Large{𝜀}$$_1,\ldots,$$\Large{𝜀}$$_n$ kautta ja osoittamalla (sopivien ehtojen vallitessa), että kaikki parin $(\mathcal{S},\mathcal{M})$ kannalta relevantit osaympäristöt $\Large{𝜀}$$_{k_1},\ldots,$$\Large{𝜀}$$_{k_l}$ tuottavat saman tilan (3.4)}. [46] Koska pari $(\mathcal{S}, \mathcal{M})$ hetkellä $t>t_d$ olisi näin efektiivisesti eristetty, eli tilan (3.4) sisältämää kietoutumista ei voitaisi identifioida mihinkään osaympäristöön $\Large{𝜀}$$_{k_i}, i=1,\ldots,l$, niin sekoitetulle tilalle (3.4) voidaan käytännössä antaa tietämättömyystulkinta, pari on jommassa kummassa puhtaassa tilassa $\hat m_i(\rho)\otimes\sigma_i^f$, $i\in\{+,-\}$.

Kvanttidarwinismin perusnäkemykset on toistaiseksi voitu työstää vain melko yksinkertaisten mallien tasolla joten on liian aikaista arvioida syntyykö tästä kvanttimekaniikalle johdonmukainen tulkinta. Se, että mittausongelman ratkaisu riippuisi keskeisesti ympäristön sattumanvaraisista ominaisuuksista vaikuttaa kuitenkin (tämän kirjoittajan näkökulmasta) epätyydyttävältä.

Kvanttidarwinismin lisäksi dekoherenssi-ilmiölle perustuvia kvanttimekaniikan tulkintahahmotelmia on vuosikymmenten varrella esitetty lukuisia. Maximilian Schlosshauerin katsausartikkeli Quantum decoherence, Physics Reports 831 (2019) 1–57, sekä Guido Bacciagaluppin tietosanakirja-artikkeli The role of decoherence in quantum mechanics, https://plato.stanford.edu/archives/fall2020/entries/qm-decoherence, ovat kattavia katsauksia aihepiiriin ja sen laajaan kirjallisuuteen.

3.3.2. Spontaani lokalisointi. Tämän otsikon alle mahtuvia kvanttimekaniikan ’tulkintoja’ on taas suuri joukko. Kysymyksessä ei varsinaisesti ole kvanttimekaniikan tulkinta vaan yritys muotoilla kvanttimekaniikan pohjalta yleisempi teoria, joka mikroskooppisella tasolla tuottaisi oleellisesti kvanttimekaniikan ennusteet ja makroskooppisella klassisen mekaniikan kuvauksen, eroten kummastakin teoriasta ’mesoskooppisella’ alueella. [47]

Näiden teorioiden kannattajille kvanttimekaniikan mittausongelma on vain yksi osoitus teorian puutteellisuudesta, johon myös seuraavien kokeellisten seikkojen katsotaan viittaavan. Nämä liittyvät havaintoihin jotka ovat ehkä selkeimmin kuvattavissa kaksoisrakokokeen avulla. Yksittäisillä mikroskooppisilla objekteilla fotoneista, elektroneista, ja neutroneista atomeihin ja suuriin molekyyleihin ja jopa tuhansista hiukkaista koostuviin nanopalloihin, suoritetuilla kaksoisrakokokeilla on todennettu kvanttimekaniikan ennustama tilastollinen interferenssikuvio, ilmiö joka pohjautuu (kvanttimekaniikan mukaan) rakojen määrittelemien erillisiin paikkoihin liittyvien puhtaiden tilojen superpositioon, niiden unitaariseen evoluutioon.[48] Nanopallojen kokoluokka on nanometrialueella. Kun vastaavia kaksoisrakokokeita tehdään mikrometriä selvästi suuremman läpimitan hiukkasilla, niin tulos on klassisen teorian mukainen; havaintolevylle kertyy kaksi erillistä läiskää, vastaten kummankin raon mahdollistamaa reittiä lähteestä varjostimelle. Väliinjäävästä kokoluokka-alueesta, jossa ikään kuin siirrytään kvanttimekaniikan pätevyysalueesta klassisen mekaniikan pätevyysalueeseen, ei tiedetä.

Unitaarinen dynaaminen evoluutio säilyttää systeemin koosta riippumatta tilojen superpositiorakenteen. Paikkalokalisoitujen puhtaiden tilojen superpositioiden tuottamisen ja ylläpitämisen vaikeus sekä tällaisten tilojen lähes täydellinen puuttuminen suurilta objekteilta osoittaa spontaanin lokalisoinnin teorian kannattajille, että unitaarinen dynamiikka on liian rajoittunut. Näiden teorioiden mukaan fysikaaliset objektit pyrkivät spontaanisti lokalisoitumaan. Ne ovat esimerkki modifioidun dynamiikan malleista joissa perusajatuksena on että makroskooppisen (monivapausasteisen) systeemin dynaaminen evoluutio sisältää välttämättä spontaaneja stokastisia prosesseja joita ei voida kuvata suljettuja (eristettyjä) systeemejä luonnehtivan unitaarisen dynamiikan keinoin. Tällainen stokastinen prosessi tulee näkyviin vain suurilla systeemeillä varmistaen että niiden tietyillä suureilla, kuten paikka- tai ylipäätään asteikkosuureilla, voitaisiin aina todeta olevan käytännöllisesti katsoen hyvin määritellyt arvot.

Yksi ensimmäisistä ja ehkä tunnetuin sponaanin lokalisoinnin malli on Ghirardin-Riminin-Weberin malli, GRW-malli, [49] joka rakentuu Hilbertin avaruus -kvanttimekaniikalle lisäten unitaariseen dynaamiseen evoluutioon satunnaisina aikoina tapahtuvan spontaanin lokalisoinnin jossa yksittäiset objektit lokalisoituvat toisistaan riippumattomasti Poissonin prosessin mukaisesti tyypillisellä intensiteetillä $\lambda_{GRW}\simeq 10^{-16}s^{-1}$ suuruusluokkaa $r_c\simeq 100\, nm$ oleville alueille. [50]

Kun fysikaalinen systeemi on pieni, eli koostuu vain muutamasta osasysteemistä, niin mallin ennusteet eivät käytännöllisesti katsoen poikkea kvanttimekaniikan ennusteista mutta makroskooppisille systeemeille (osasia esim. luokka $10^{23}$) lokalisoinnin yhteisvaikutus on ylivertainen, tehden makroskooppisen systeemin paikkasuureesta joka hetki objektiivisen. Teorian sisältämät parametrit $\lambda_{GRW}$ ja $r_c$ ovat uusia luonnon vakioita joiden arvot kiinnitetään viimekädessä kokeellisesti.

Spontaanin lokalisoinnin teorioiden voi perustellusti sanoa ratkaisevan mittausongelman ja eliminoivan ad hoc projektiopostulaatin. Ilman selkeää käsitteellistä perustelua dynamiikan muuttamiseksi, ratkaisu on kuitenkin itsessään ad hoc. Koska unitaarisen dynamiikan taustalla on selkeät hyvin tunnetut symmetriaperiaatteet, niin on ilmeistä että ratkaisu edellyttää myös uusien symmetriaperiaatteiden muotoilemisen. Spontaanin lokalisoinnin aiheuttaja on myös avoin kysymys; sekä lämpöliikettä että gravitaatiota on ehdotettu prosessin syyksi. Alan tutkimus (ks. alaviite 47) on vireää mutta on vielä liian aikaista muodostaa asiassa selkeä kanta. On kuitenkin syytä korostaa, että mitkään näistä malleista eivät, ainakaan niiden kehittelyn tässä vaiheessa, pysty tuottamaan kuin vain pienen osan kvanttimekaniikan tuloksista, kuten atomien spektraalirakenne. Koska spontaanin lokalisoinnin mallit johtavat ’mesoskooppisella’ alueelle kvanttimekaniikasta poikkeaviin ennusteisiin, niin mallien mahdollinen kokeellinen pätevyys on myös keskeinen avoin kysymys. [51]

3.4. Muuta. Kvanttimekaniikalle on esitetty lukuisia eri tulkintahahmotelmia edellä kuvattujen lisäksi ja näistäkin useimmat ovat tulkintaryhmiä joiden sisällä on suurta variaatiota. Esittelen vielä lopuksi kaksi uudempaa tulkintakehitelmää, relationaalinen kvanttimekaniikka sekä QBismi jotka molemmat ovat saaneet osansa huomiotaloudesta.

Alaviitteessä 4 mainittiin lyhyesti kvanttimekaniikan ns. silminnäkijä-tulkinta, jonka perusajatus on, että vuorovaikutukset määrittävät systeemien kulloisetkin ominaisuudet systeemien omaaman erityisen kaksipuolisen tilatarkkailumekanismin (witnessing) kautta joka myös johtaa tilan romahdukseen tarkkailutulosta vastaavaksi. Kvanttimekaniikan relationaalisessa tulkinnassa perusajatus on oleellisesti sama mutta se pyrkii välttämään projektiopostulaatin relativoiden tilakäsitteen havaitsijakohtaiseksi. Tulkinta on pääasiassa Carlo Rovellin käsialaa [52] ja se on saanut melkoisesti julkisuutta mm. Rovellin yleisluonteisen kirjan Helgoland: making sense of the quantum revolution ilmestyttyä 2020. Kirja sisältää lyhyen sujuvan yleistajuisen historiallisen katsauksen kvanttimekaniikan syntyyn ja sen alkuperäistulkinnan hahmottumiseen sekä siihen liittyvistä ongelmista. Kirja etenee esittelemällä relationaalisen tulkinnan, jonka tekijä katsoo ratkaisevan kvanttimekaniikan tulkintaongelman. Huolellinen kriittinen analyysi kuitenkin osoittaa, että väite ei ole ongelmaton sillä välttääkseen tilaromahduksen havaitsijakohtaisuudesta aiheutuvan solipsismin tulkintaa on jouduttu täydentämään olettamuksilla, [53] jotka palauttavat havaitsijakohtaisen tilaromahduksen havaitsijasta oleellisesti riippumattomaksi tilan romahdukseksi, projektiopostulaatiksi. [54] Jää nähtäväksi kehittyykö tästä kvanttimekaniikalle varteenotettava tulkinta.

QBismi on todennäköisyyden subjektiiviselle tulkinnalle perustuva kvanttimekaniikan tulkinta joka hyväksyy sekä teorian yleispätevyyden että myös tilan ’romahduksen’ mittauksessa joka on tässä katsannossa vain havaitsijan luonnollinen tilapäivitys saamansa uuden tiedon pohjalta.

Tulkinnan yksi näkyvimmistä kehittäjistä ja puolestapuhujista on Chris Fuchs. [55] Tulkinnan pyrkimyksenä on muotoilla kvanttimekaniikan todennäköisyysväittämät $p^\mathsf{E}_\rho(X)$ bayesiläisittain ehdollisina todennäköisyyksinä ehdollistettuna havaitsijan tiedoilla systeemistä, tiedoilla tai uskomuksilla jotka hän, havainnoija, ilmaisee tilan käsitteellä.

QBismin lähtökohtana on se tosiasia, että tila $\rho$ määräytyy todennäköisyysmitoista $p^\mathsf{E}_\rho, \mathsf{E}\in \boldsymbol{O}$ (kaikkien suureiden joukko) ja että tähän riittää yksi suure (mittaus) $\mathsf{F}$ kunhan se on informatiivisesti täydellinen, eli erottaa tilat toisistaan: kaikilla $\rho,\gamma$, jos $p^\mathsf{F}_\rho=p^\mathsf{F}_\gamma$, niin $\rho=\gamma$ (vrt alaviite 7). Niinpä tilan tulkinta $\rho$ voidaan kytkeä todennäköisyysmitan $p^\mathsf{F}_\rho$ tulkintaan.

Fysikaalisen suureen informatiiviselle täydellisyydelle on useita yhtäpitäviä luonnehdintoja. Vaikka tällaisia suureita osataan konstruoida ja myös kokeellisesti implementoida, niin tilan tosiasiallinen määrittäminen tilan ja suureen määrittelemistä todennäköisyyksistä on yleensä hyvin monimutkaista. On kuitenkin olemassa äärellistasoisia fysikaalisia systeemejä, (systeemejä joiden kuvaus perustuu äärellisulotteiselle, $d$-ulotteiselle Hilbertin avaruudelle (K1 Liite),) joille voidaan muodostaa ns. symmetrisiä informatiivisesti täydellisiä suureita (mittauksia), joissa tilan rekonstruktio (atomaarisista) todennäköisyyksistä $p^\mathsf{F}_\rho(\{i\}), i\in\Omega,$ voidaan helposti toteuttaa. [56]

Olkoon $\mathcal{S}$ sellainen $d$-tasosysteemi jolle on olemassa sellainen puhtaiden tilojen (yksiulotteisten projektioiden) joukko $\rho_1, \ldots ,\rho_{d^2}$, joille pätee (symmetriaehto) $tr{[\rho_i\rho_j]}=\frac 1{d+1}, i\ne j$. Efektit $F_i=\frac 1d\rho_i, i\in\Omega= \{1, \ldots ,d^2\},$ määrittelevät suureen $\mathsf{F}$ ehdosta $\mathsf{F}(\{i\})=F_i$. Suure on informatiivisesti täydellinen. Lisäksi tila $\rho$ voidaan lausua suureen $\mathsf{F}$ ja sen mittaustulostodennäköisyyksien avulla muodossa

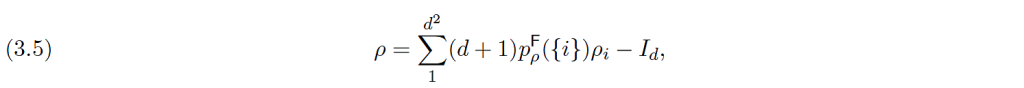
missä $I_d$ on ($d$-ulotteisen avaruuden) identiteettioperaattori. Tilan $\rho$ subjektiivinen tulkinta syntyy siitä, että todennäköisyyksien $p^\mathsf{F}_\rho(\{i\})$ katsotaan nyt edustavan havainnoijan (agentin) priori todennäköisyyksiä, uskomuksia, tarkastelemastaan systeemistä, ja hän voi halutessaan varmistaa ne referenssimittauksella $\mathsf{F}$. Näiden pohjalta hän muodostaa ’vedonlyöntisuhteensa’ kyseisen systeemin minkä tahansa suureen $\mathsf{E}$ mahdollisista mittaustuloksista kytkemällä todennäköisyydet $p^\mathsf{E}_\rho(X)$ bayesiläiseen kokonaistodennäköisyyden lausekkeeseen. [57]

Mikä tahansa $\mathsf{F}$-mittaus on informatiivisesti täydellinen, mutta Bornin todennäköisyyksien kytkeminen bayesiläisiin todennäköisyyksiin vaatii paitsi sen että mittaus on teorian puitteissa kuvattavissa niin myös sen että mittauksen synnyttämät ehdolliset tilamuunnokset $\rho\mapsto\hat m_i(\rho)$ ovat sellaisia, että $\hat m_i(\rho)=\rho_i$. Vaikka suure $\mathsf{F}$ ei ole tarkka [$F_i^2=(\frac 1d\rho_i)^2=\frac 1{d^2}\rho_i \leq F_i$], niin sille voidaan kuitenkin konstruoida tällainen mittaus, ns. yleistetty Lüdersin mittaus, jolle $\rho^f=\hat m_\Omega(\rho)=\sum p^\mathsf{F}_\rho(\{i\})\hat m_i(\rho)= \sum p^\mathsf{F}_\rho(\{i\})\rho_i$, jolloin komponenttitilat $\hat m_i(\rho)$ ovat tarkalleen suureen $\mathsf{F}$ efektien määrittelemät puhtaat tilat $\rho_i$. [58] Tämä kaikki johtuu efektien $F_i$ erikoislaatuisuudesta. Kuten aiemmin jaksossa 2.2.1 on jo ollut esillä, todennäköisyys $p^\mathsf{E}_{\hat m_i(\rho)}(X)$ on todennäköisyys sille että suureen $\mathsf{E}$ mittaus johtaa tulokseen joukosta $X$ ehdolla, että ensin tilassa tilassa $\rho$ suoritettu $\mathsf{F}$ mittaus tuottaa asteikkolukeman $i$. Kun merkitään tätä ehdollista todennäköisyyttä symbolilla $p(\mathsf{E}(X)|i)$ ja huomataan, että $p(\mathsf{E}(X)|i)=p^\mathsf{E}_{\rho_i}(X)$, niin saamme tuloksen

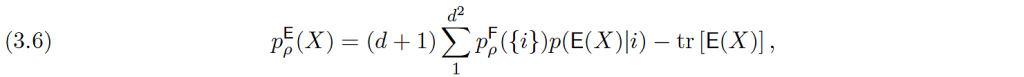
joka osoittaa, että suureen $\mathsf{E}$ mittaustulostodennäköisyydet $p^\mathsf{E}_\rho(X)$ tilassa $\rho$ ovat oleellisesti (vakiotermiä $(d+1)$ ja lukua $tr{[\mathsf{E}(X)]}$ vaille) bayesiläinen kokonaistodennäköisyys $\sum_1^{d^2}p^\mathsf{F}_\rho(\{i\})p(\mathsf{E}(X)|i)$. Merkintä $p(\mathsf{E}(X)|i)$ peittää alleen sen tosiasian, että kyseinen ehdollinen tulkinta edellyttää suureen $\mathsf{F}$ mittauksen $\mathsf{M}$ spesifiointia, ja siis erityisesti myös mittalaitteen $\mathcal{M}$ alkutilan $\sigma$ kiinnittämisen. Toisin sanoen, havainnoijalla pitää olla priori tieto myös käyttämästään mittalaitteesta, erityisesti sen alkutilasta. Tähän liittyvien uskomusten varmistaminen puolestaan näyttäisi edellyttävän vastaavaa mittaussarjaa synnyttäen päättymättömän mittausketjun.

Bornin lausekeen palauttaminen bayesiläiseksi kokonaistodennäköisyyden lausekkeeksi on yleisesti ottaen avoin kysymys. Voidaan myös kysyä missä mielessä tila esittää yksittäisen havaitsijan uskomuksia hänen henkilökohtaisista odotuksistaan mahdollisesti suorittamilleen mittauksille kun tilan (3.5) priori todennäköisyydet $p^\mathsf{F}_\rho({i})$ sekä lausekkeen (3.6) edellyttämä yleistetty Lüdersin mittaus ovat kaikille havainnoille (agenteille) samat, tai ainakin ekvivalentit jos kaikki agentit tunnistavat tarkasteltavan systeemin samaksi $d$-tasosysteemiksi. Mutta tällöin tulkinta olisikin intersubjektiivinen. [59] Tämä taas vastaa paremmin paitsi kokeellista käytäntöä niin myös fysiikan perustavoitteita objektiivisen fysikaalisen todellisuuden kuvaamiseksi.

Lopuksi

Kvanttimekaniikan matemaattinen ja käsitteellinen perusta tunnetaan varsin hyvin, teoriaa on menestyksellisesti sovellettu kohta jo sata vuotta ja usko uuteen kvanttiteknologiaan on vahva. Tähän kaikkeen riittää minimitulkittu kvanttimekaniikka. Jos kuitenkin yritämme hahmottaa tieteellistä maailmankuvaa kvanttimekaniikan pohjalta niin kohtaamme ilmeisiä vaikeuksia jotka kulminoituvat teorian aitoon todennäköisyysluonteeseen ja kvanttikietoutumiseen sekä näiden piirteiden yhteensopimattomuuteen arkikokemuksen kanssa; von Wrightin sanoin ”fysiikan käsitettävyyden klassiset mallit näyttävät luhistuneen”. Mutta mitä ovat ne uudet tieteellisen käsitettävyyden mallit joita kvanttimekaniikan tulkintaan kohdistunut laaja tutkimus on nostanut esille?

Ajatus klassiseen fysiikkaan perustuvan klassisen kielen välttämättömyydestä kvantti-ilmiöiden kuvaamiseksi on tässä suhteessa varsin konservatiivinen ja se johtaa vaikeaan kysymykseen kyseisten teorioiden pätevyysalueista. Toistaiseksi tuntuu myös varsin etäiseltä, että neurotieteiden kehitys johtaisi havainto-ongelman ratkaisuun havaitsijan tietoisuuden kvantitatiivisen ymmärtämisen kautta esimerkiksi Orch OR mallin mukaisesti. Mullistava uusi käsitettävyyden moodi on maailman jatkuva jakautuminen rinnakkaisiin, riippumattomiin todellisuuksiin, mutta ratkaiseeko tämä kvanttimekaniikan synnyttämän ymmärrettävyyden kriisin vai siirtääkö se ongelman vain toisaalle? Modaalitulkintojen pyrkimys lieventää varmaan ennustettavuuteen perustuvaa todellisuusehtoa on mielenkiintoinen mutta onko se tyydyttävä: mittauksessa epäobjektiivinen suure kyllä objektivoituu mutta tiedämme sen arvon vain alkuperäisellä todennäköisyydellä.

Fysiikan keskeisiä metodologisia periaatteita ovat mahdollisuus jakaa maailma tarkastelua varten osiin (systeemi, mittalaite, ympäristö, $\ldots$) ja vaatimus kokeen ajallis-paikallisesta toistettavuudesta. Jos ympäristön vaikutusta ei voida kuitenkaan täysin eliminoida tai edes kontrolloida ja jos objektivointiongelmaan saadaan vain ympäristön sattumanvaraisesta rakenteesta johtuva käytännöllinen ratkaisu, niin kyseiset periaatteet ovat uhattuina.

Kvanttimekaniikan rajoittuneesta pätevyysalueesta ei ole olemassa kokeellista näyttöä mutta pitäisikö kvantti-ilmiöiden puuttuminen makroskooppisella tasolla kuitenkin tulkita teorian riittämättömyydeksi varsinkin kun kysymys kvanttimekaniikan klassisesta rajasta on vielä auki? Gravitaation, taustasäteilyn tai lämpöliikkeen mahdollisesti aiheuttaman kvanttiobjektien spontaanin lokalisoinnin varaan on kuitenkin ennenaikaista laskea. On myös epäselvää johtaisiko käsitteen ”todennäköisyys” vaihtaminen käsitteeksi ”informaatio” tai QBismin hengessä Bornin objektiivisten todennäköisyyksien muotoilu bayesiläisittäin havaitsijan vedonlyöntisuhteiksi uusiin käsitettävyyden malleihin.

Kvanttimekaniikan tulkintavaihtoehtoja on tutkittu valtavasti ja sen minimitulkinnan yli tai ohi menevistä tulkintalinjoista on kasvanut keskenään kiisteleviä koulukuntia. Jää nähtäväksi tuoko kvanttitilaskentaa hyödyntävä tekoäly ongelmaan lopullisen ratkaisun!

---

Kirjoitukseni on monin tavoin hyötynyt kollegojeni dosentti Juha-Pekka Pellonpään  ja professori emeritus Kari Ylisen  kanssa käymistäni keskusteluista.  

Kiitos myös FM Tuomo Riekkiselle sujuvasta taittotyöstä.

---

Viitteet

[1] Kvanttimekaniikan lopullisena läpimurtona ja siis syntymäpäivänä voidaan pitää N/A.12.1925, joilloin Werner Heisenbergin tutkimus ’Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen’ ilmestyi aikakauskirjassa Zeithscrift für Physik 33 (1925) 879-893; tutkimus, joka johti kvanttimekaniikan matemaattisen rakenteen keksimiseen ns. matriisimekaniikan muodossa. Synnytysprosessi kesti lähes päivälleen neljännesvuosisadan siitä kun Max Planck antoi 14.12.1900 Saksan fyysikkoseuran kokouksessa hieman aiemmin keksimälleen ns. mustan kappaleen, kuuman uunin, seinämien säteilyn spektrin matemaattiselle lausekkeelle selityksen: uunin seinämien värähtelijät eli atomit luovuttavat ja vastaanottavat energiaa vain epäjatkuvina hyppäyksinä, energiakvantteina. Planck itse piti tätä mielestään epätoivoiselta tuntuvaa selitystä väliaikaisena.

[2] Ks. esim. M. Suleymanin, M. Bhaskarin, The Coming Wave, Penguin, 2023, https://www.ibm.com/thoughtleadership/institute-business-value/report/quantum-decade, tai kirjoitus https://www.vttresearch.com/fi/uutiset-jatarinat/suomen-toinen-kvanttitietokone-valmistunut (poimittu 10.10.2023).

[3] Kaikki kvanttimekaniikan tulkinnat eivät jaa tätä pyrkimystä.

[4] Lyhenne K2.4.2 viittaa aiemman Dimension artikkelin K2 lukuun 4.2.

[5] On syytä korostaa, että tällaiset ristiriidat syntyvät kun kvanttimekaniikkaa yritetään täydentää joillakin tyypillisesti klassisesti motivoiduilla lisäolettamuksilla. Ne eivät ole kvanttimekaniikan ristiriitoja, mutta asettavat rajoja teorian tulkinnoille.

[6] Ks esim. Henk W. De Regt, Understanding scientific understanding, Oxford University Press, 2017.

[7] Taustalla on siis ajatus, että toistokokeista saadut ‘suotuisten tapausten’ suhteelliset frekvenssit approksimoivat näitä todennäköisyyksiä. On syytä korostaa, että tämä ei ole kannanotto todennäköisyyden mahdolliselle tulkinnalle. Muistettakoon myös (K1.2), että teoriaan on sisäänrakennettu tilastollinen täydellisyys, jolloin erityisesti tilat $s$ voidaan samaistaa todennäköisyyksien $p^O_s, O\in \boldsymbol{O}$, kokonaisuuteen, ja tilan merkitys voidaan näin liittää myös todennäköisyyden merkitykseen.

[8] Ajatus on peräisin Paul Diracilta (1930), sen matemaattinen muotoilu V.S. Varadarajanilta (1968).

[9] Suurempaa konkretiaa kaipaava lukija voi halutessaan tulkita tällaiset suureet artikkelin K1 kubittisuureina.

[10] Eräät kvanttimekaniikan tulkinnat kiistävät myös varmaan ennustettavuuteen perustuvan realistisen puhetavan.

[11] Todennäköisyyden subjektiiviset tulkinnat eivät poista sitä matemaattista tosiasiaa, että puhtaisiin tiloihin liittyviä epätriviaaleja ($\ne 0,1$) todennäköisyyksiä ei voida palauttaa 0 – 1 -todennäköisyyksiin. Sekoitettujen tilojen monikäsitteinen esitys puhtaiden tilojen avulla vain korostaa tätä tulosta.

[12] M. Born, Zur Quantenmechanik der Stoßvorgänge, Z. Physik 37 (1926) 863-867.

[13] The Born-Einstein letters : correspondence between Albert Einstein and Max and Hedwig Born from 1916-1955, with commentaries by Max Born, London, Macmillan, 1971.

[14] Jos kvanttimekaniikka on yleispätevä perusteoria, kuten usein ajatellaan, niin näin luonnollisestikin on.

[15] On syytä korostaa, että teoria perustuu sille metodologiselle olettamukselle, että tutkittava systeemi $\mathcal{S}$ ja mittalaite $\mathcal{M}$ sekä niiden muodostama yhdiste $(\mathcal{S}, \mathcal{M})$ voidaan eristää muusta (fysikaalisesta) maailmasta.

[16] Lisäksi asteikkosuure $\mathsf{Z}$ voidaan aina valita tarkaksi suureeksi, alkutila $\sigma$ puhtaaksi tilaksi, sekä mittausvuorovaikutus $V$ unitaariseksi, siis $V(\rho\otimes\sigma)=U(\rho\otimes\sigma)U^*$, jollekin unitaarikuvaukselle $U: \mathcal{H}\otimes \mathcal{K}\to \mathcal{H}\otimes \mathcal{K}$.

[17] Yhtäpitävästi, jonotodennäköisyys $p^\mathsf{F}_{\hat m_X(\rho)}(Y)p^\mathsf{Z}_{\sigma^f}(X)$ on sama kuin todennäköisyys sille, että kaksoissuureen $(\mathsf{F}, \mathsf{Z})$ mittaus systeemillä $(\mathcal{S}, \mathcal{M})$ tilassa $V(\rho\otimes\sigma)$ tuottaa tulosparin (karteesisesta) tulojoukosta $Y\times X$; kaavana, $p^\mathsf{F}_{\hat m_X(\rho)}(Y)p^\mathsf{F}_{\sigma^f}(X) = p^{\mathsf{F}\otimes \mathsf{Z}}_{V(\rho\otimes\sigma)}(Y\times X)$.

[18] Toisin kuin hajotelma (2.1), tämä komponenttitilahajotelma saadaan aina (kaikilla $\mathsf{M}$) mutta komponenttitilat eivät välttämättä ole suureen $\mathsf{E}$ ominaistiloja, saatikka muotoa $p^\mathsf{E}_\rho(\{\pm\})^{-1} E_\pm\rho E_\pm$.

[19] Tässä ilmenee se seikka että myös kvanttimekaniikan mukaan systeemiä mitenkään muuttamatta voidaan saada selville mitä ominaisuuksia (suureiden arvoja) systeemillä tietyssä tilassa on (probabilistisen varmuuden mielessä); vrt. jakson K2.4.2. todellisuusehto (R).

[20] Huomaa, että tämä vaatimus ei vaikuta mitenkään alisysteemitiloihin (2.1) ja (2.2).

[21] Taustalla on kohteen metodologinen jako kolmeen osaan: tutkittava systeemi, mittalaite, ympäristö. Jos mittalaitetta, sen relevanttia osaa, ei voida täysin eristää ympäristöstä niin sekoitettu tila olisi luonnollinen lähtötila.

[22] Ks. esim. P. Busch, Can ‘Unsharp Objectification’ Solve the Quantum Measurement Problem?, Int J Theor Phys 37 (1998) 241–247.

[23] Vrt. alaviite 15.

[24] Tulkinta kuuluu lähinnä kvanttimekaniikan historiaan, eräänä reaktiona Albert Einsteinin, yhdessä Boris Podolskyn ja Nathan Rosenin kanssa, esittämälle kvanttimekaniikan epätäydellisyyskritiikille, K2.4.

[25] Piilomuuttujan valinta riippuu siitä mikä suure tulkitaan ’klassiseksi’ suureeksi, kaikkia ei voida näin valita. Tyypillisesti tämä on paikkasuure.

[26] Filosofi Paavo Pylkkänen on ns. bohmilaisen mekaniikan pitkän linjan suomalainen asiantuntija. Hänen ja muiden bohmilaisen tulkinnan kehittäjien ajatuksiin voi paneutua mm. kirjoituskokoelmassa: Jan Walleczek , Gerhard Grössing, Paavo Pylkkänen and Basil Hiley, Emergent Quantum Mechanics: David Bohm Centennial Perspectives, Entropy 21 (2019) 113. Myös Detlef Dürrin ja Dustin Lazarovicin teos Understanding Quantum Mechanics: the world according to modern physics, Springer, 2020, on voimakas puheenvuro bohmilaisen mekaniikan puolesta. Vaikka teorialla on vankka kannattajakuntansa niin on kuitenkin huomattava, että sen selitysvoima on vielä varsin heikko esimerkiksi atomi- ja molekyylifysiikassa, joka on kvanttimekaniikan keskeisiä sovellusaloja.

[27] Termi ”Kööpenhaminan tulkinta” esiintyy ilmeisesti ensimmäisen kerran vuonna 1955 Werner Heisenbergin artikkelissa The development of the interpretation of the quantum theory kokoomateoksessa Niels Bohr and the development of physics (1955) ja laajemmin kirjassa Physics and Philosophy (1958), jonka luvun luvun III otsikko on The Copenhagen Interpretation of Quantum Theory. Ns. Chicago-luennoissaan vuonna 1929 Heisenberg toivoi levittävänsä kvanttiteorian Kööpenhaminan henkeä, ”Kopenhagener Geist der Quantentheorie”.

[28] Google Scholar antaa hakusanalle Copenhagen interpretation 1 010 000 viitausta, poimittu 28.11.2023.

[29] Näiden keskustelujen tuloksina syntyivät artikkelit N. Bohr, The Quantum Postulate and the Recent Development of Atomic Theory, Nature 121 (1928) 580-590, ja W. Heisenberg, Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik, Z. Physik 43 (1927) 172–198.

[30] von Weizsäcker, teoksessa Quantum Theory and Beyond, 1971. Bohrin omin sanoin: ”The quantum theory is characterized by the acknowledgment of a fundamental limitation in the classical physical ideas when applied to atomic phenomena. The situation thus created is of a peculiar nature, since our interpretation of the experimental material rests essentially upon the classical concepts.” (Bohr, alaviite 29). Heisenbergin vastaava muotoilu on selkeimmin luettavissa hänen 1958-kirjansa luvun III alusta, alaviite 27.

[31] Useimmat näistä kirjoituksista sisältyvät Bohrin artikkelikokoelmiin Atomic Theory and the Description of Nature, Atomic Physics and Human Knowledge, ja Essays 1958-1962 on Atomic Physics and Human Knowledge vuosilta 1934, 1958, ja 1963, vastaavasti. Aihepiirin sekundäärinen kirjallisuus on hyvin laajaa, mainittakoon vain teokset H.J. Folse, The philosophy of Niels Bohr: The framework of complementarity, Elsevier Science Pub. Co.,1985, ja Arkady Plotnitsky, Niels Bohr and Complementarity: An introduction, Springer, 2012.

[32] N. Bohr, Causality Problems in Atomic Physics, teoksessa New Theories in Physics, Paris, 1939, pp. 11-45.

[33] Katso esim. K1, Taustatietoa 1.

[34] Nimitys projektiopostulaatti on peräisin artikkelista H. Margenau, Philosophical Problems concerning the Meaning of Measurement in Physics, Philosophy of Science 25, 23-33, 1958.

[35] S. Kochen, A new interpretation of quantum mechanics, teoksessa Symposium on the Foundations of Modern Physics 1985, P. Lahti and P. Mittelstaedt, eds., World Scientific, ss. 151-169.

[36] Everettin vuonna 1957 aikakauslehdessä Reviews of Modern Physics julkaisema yllä mainittu artikkeli on typistetty versio hänen väitöskirjastaan The theory of the universal wave function (1956), joka julkaistiin vasta DeWittin ja Grahamin kirjassa, ibid. Everettin työn tieteenhistoriankin näkökulmasta varsin erikoisista vaiheista voi lukea Jeffrey A. Barrettin ja Peter Byrnen teoksesta The Everett Interpretation of Quantum Mechanics : Collected Works 1955-1980 with Commentary, Princeton University Press, 2012. Siirryttyään väitöskirjansa jälkeen yliopistomaailman ulkopuolisiin tehtäviin Everett ei varsinaisesti kommentoinut tulkintansa uudelleen tulkintoja eikä osallistunut niiden jatkokehittelyihin.

[37] Everettin käyttämä ’tiedostavan havaitsijan’ kieli ei tässä ole oleellinen; se voidaan korvata automaatilla, joka kykenee tallentamaan muistijonoja.

[38] Väitöskirja, sivu 68.

[39] W. Ochs, On the strong law of large numbers in quantum probability theory, J Phil Logic 6 (1977) 473-480; B.S. Witt, The many-universes interpretation of quantum mechanics, Proceedings of the International School of Physics ‘Enrico Fermi’, Academic Press, 1971.

[40] Ks. esim. konferenssin The Many-Worlds Interpretation of Quantum Mechanics, 2022, kokoomajulkaisua osoitteessa https://www.mdpi.com/journal/quantumrep/specialissues/MWI, poimittu 26.4.2024.

[41] Tilojen $V(\rho\otimes\sigma)$, $\sigma^f$, $\rho^f$ asiaan kuuluvien rakenneominaisuuksien suhteen voidaan helposti määritellä useita ”luonnollisia” näissä tiloissa mahdollisten ominaisuuksien joukkoja.

[42] Aiheesta laajemmin esim. P. Busch, P. Lahti, P. Mittelstaedt, The Quantum Theory of Measurement, 2nd revised edition, 1996, luku IV.5, tai J. Bub, Interpreting Quantum World, Cambridge UP, 1997, luku 6.2.

[43] Eristetyn systeemin dynaaminen kehitys voidaan aina antaa unitaarisena.

[44] Ilmiö on luonnollisesti sama kuin tilan $\rho$ muuntuminen mittauksessa $\mathcal{M}$ tilaksi $\hat m(\rho)=p^\mathsf{E}_\rho(\{+\})\hat m_+(\rho)+p^\mathsf{E}_\rho(\{-\})\hat m_-(\rho)$.

[45] Kvanttidarwinismi rakentuu ensisijaisesti Wojciech Zurekin tutkimuksille joissa mittausongelmaa on pyritty ratkaisemaan juuri ympäristön aiheuttaman dekoherenssi-ilmiön pohjalta. Zurekin artikkeli Quantum Darwinism, Nature Physics 5 (2009) 181-188, on hyvä katsaus aihepiiriin ja sen alkuperäislähteisiin. Tulkinnan nimellä halutaa korostaa sitä, että kysymyksessä on eräänlainen luonnollinen evoluutio.

[46] Ks. esim. J.K. Korbicz, Roads to objectivity: quantum darwinism, spectrum broadcast structures, and strong quantum darwinism–a review. Quantum 5 (2021) 571.

[47] Artikkeli Bassi, A., Lochan, K., Satin, S., Singh, T. P., \& Ulbricht, H., Models of wave-function collapse, underlying theories, and experimental tests, Reviews of Modern Physics 85 (2013) 471, on kattava katsaus näihin teorioihin

[48] Ks. esim, S.Gerlich et al, Quantum interference of large organic molecules, Nature communications 2:263 (2011); M. Arndt, K. Hornberger, Testing the limits of quantum mechanical superpositions, Nature Physics 10 (2014) 271-277.

[49] G.C. Ghirardi, A. Rimini, T. Weber, Phys. Rev. D 34 (1986) 470.

[50] Teknisesti, ja yksinkertaistaen, $N$-hiukkastila $\rho$ kokee unitaarisen evoluution $t\mapsto V_t(\rho)$ lisäksi kunkin yksittäisen osasysteemin osalta satunnaisen toisistaan riippumattoman tilaromahduksen, sumean Gaussisen lokalisoinnin, $\rho_t\mapsto \lambda_{GRW}\int_R L_{q}\rho_tL_{q}^*\,dq,$ missä $L_{q}= (\pi r_c^2)^{-1/4}e^{-(\mathbf Q-q)^2/2r_c^2}$, $\mathbf Q$ kyseisen osasysteemin paikkaa (avaruudessa $\mathbb{R}^3$) edustava operaattorikolmikko $(Q_1,Q_2,Q_3)$ ja $\boldsymbol{q}=(q_1,q_2,q_3)\in \mathbb{R}^3$ piste jossa lokalisointi tapahtuu.

[51] Alaviitteen 47 lisäksi, ks. esim. S. Nimmrichter, K. Hornberger, P. Haslinger, M. Arndt, Testing spontaneous localization theories with matter-wave interferometry, Phys. Rev. A 83, 043621 (2011), sekä S. Donadi, K. Piscicchia, C. Curceanu, L. Diósi, L.,M. Laubenstein, A. Bassi, Underground test of gravity-related wave function collapse, Nature Physics 17 (2021) 74-78.

[52] C. Rovelli, Relational Quantum Mechanics, Int. J. Theor. Phys. 35 (1996) 1637, ja esim. C. Rovelli, Space is blue and birds fly through it, Phil. Trans. R. Soc., A 376 (2017).

[53] E. Adlam, C. Rovelli, Information is Physical: Cross-Perspective Links in Relational Quantum Mechanics, arXiv:2203.13342v2.

[54] P. Lahti, J.P. Pellonpää, An attempt to understand relational quantum mechanics, Int J Theor Phys, 62 (2023) 170.

[55] Ks. esim. C.A. Fuchs, B.C. Stacey, QBism: Quantum theory as a hero’s handbook, teoksessa Proceedings of the International School of Physics ’Enrico Fermi ’ 197 (2019) 133-202. Ks. myös R. Healey, Quantum-Bayesian and pragmatist views of quantum theory, verkko-osoitteessa https://plato.stanford.edu/archives/win2016/entries/quantum-bayesian/, joka johdattaa myös alan alkuperäiskirjallisuuteen, sekä J.B. DeBrota ja B. Staceyn artikkeli FAQBism, arXiv preprint arXiv:1810.13401, 2018, joka puolestaan antaa lyhyitä ytimekkäistä vastauksia QBismin peruskysymyksiin.

[56] On avoin kysymys onko tällainen suure olemassa kaikilla äärellistasoisilla systeemeillä.

[57] ”To be a QBist is to use quantum theory to be a “better bettabilitarian” in this world in which we are all immersed and which we shape with our every action”, Fuchs ja Stacey, alaviite 55.

[58] Vaikka mittaus muistuttaa tarkan suureen ihanteellista toistavaa mittausta, niin tässä komponenttitilat $\rho_i$ eivät ole keskenään ortogonaalisia, $tr{[\rho_i\rho_j]}=\frac {\delta_{ij}+1}{d+1}$, eivätkä ne ole suureen $\mathsf{F}$ ominaistiloja, $tr{[\rho_iF_i]}=\frac 1d$.

[59] Ks. myös M. Ozawa, Intersubjectivity of outcomes of quantum measurements. arXiv preprint arXiv:1911.10893. Vrt. myös Huomautuksen [4] Orch OR teoriaa koskevaa vastaavaa huomiota.