Millainen oli matematiikan valtakunnallinen koe 1980-luvulla?
Oletko koskaan pohtinut, millaisia olivat matematiikan kokeet 1980-luvulla? Elettiinkö 7.–9. luokkien opetuksessa tuolloin koulumatematiikan kulta-aikaa vaatimustasoa ja osaamista ajatellen? Esittelen artikkelissa matematiikan valtakunnallisen 9. luokan kokeen vuodelta 1985 ja esitän samalla subjektiivisia huomioita siitä, miltä vaatimustaso näyttää tämän päivän näkökulmasta katsottuna. Pohdintojen tueksi tarjolla on myös yhteenveto oppilaiden silloisesta koemenestyksestä.
Vuoden 1985 koetehtävät ovat niin sanotusta tasokurssittomasta kokeesta eli sen suorittaneita oppilasryhmiä ei enää muodostettu taitotason ja opiskelumotivaation mukaisesti peruskoulun yläluokilla – kuten ei nykyäänkään. Tällaisia kokeita MAOL ry:n kustannusyhtiö MFKA-Kustannus Oy toimitti kouluihin 80-luvun puolivälin molemmin puolin muutamina vuosina. Lisäksi kokeita laadittiin vielä tuohon aikaan kolmen tasokurssin (yleiskurssi, keskikurssi, laaja kurssi) tarpeisiin. Ilmeisesti tasokurssitonta toteutustapaa kokeiltiin osassa kouluja ennen kuin tasokurssien lakkautus astui voimaan. Joka tapauksessa: on ollut kokeenlaatijoilla kiireisiä vuosia! 1980-luvulla myös fysiikan ja kemian valtakunnallisia kokeita teetettiin suurilukuisella oppilasjoukolla nykypäivään verrattuna.
Vuoden 1985 matematiikan valtakunnallisen kokeen ohjeistus opettajalle on lyhyt ja mahtuu arvosteluasteikkoineen yhdelle A4-sivulle. Koeajaksi annetaan 90 minuuttia ja laskinta saa käyttää. Mielenkiintoisena ja jopa edistyksellisenä ratkaisuna kukin koetehtävä sisältää helpoksi katsotun a-kohdan, joiden täydellinen osaaminen ilman muita pisteitä toisi hyväksytyn arvosanan 5,5. Kaikkiaan tehtäviä on tarjolla yhdeksän kappaletta, mutta näistä on suoritettava vain kahdeksan. Tehtäväkohtainen maksimipistemäärä on tuttuun ja turvalliseen tapaan kuusi. Arviointiasteikko on yllätyksetön: viidesosa pisteistä riittää läpäisyyn ja puolet maksimipistemäärästä tuo seiskan.
Alkupään tehtävät: aikaa kestäviä perustehtäviä
Ensimmäinen tehtävä on sinänsä tasoltaan sellainen, että se voisi tänä päivänäkin ehkä c-kohdan neliöjuurilaskua lukuun ottamatta esiintyä matematiikan valtakunnallisessa kokeessa. Toisaalta nykyään etenkin valtakunnallisen kokeen alussa on jonkin verran tehtäviä, joiden ratkaiseminen onnistuu alakoulutaidoilla. Tässä edetään suoraan yläkoulutasoisiin asioihin – toki laskimen käytön taitavat hyötyvät siitä merkittävästikin. Vuodet opettajana ovat osoittaneet sen, että varsin usein tehtävän 1b)-kaltaiset laskut tuottavat haasteita oppilaille, kun ajallinen etäisyys murtolukujen opiskelusta kasvaa. Lisäksi on todettava, ettei tällä hetkellä voimassa olevien päättöarvioinnin kriteerien mukaan tehtävää 1b) voitane lukea tätä nykyä perustehtäviin, vaan kyse on noin kahdeksikon tason osaamisesta.
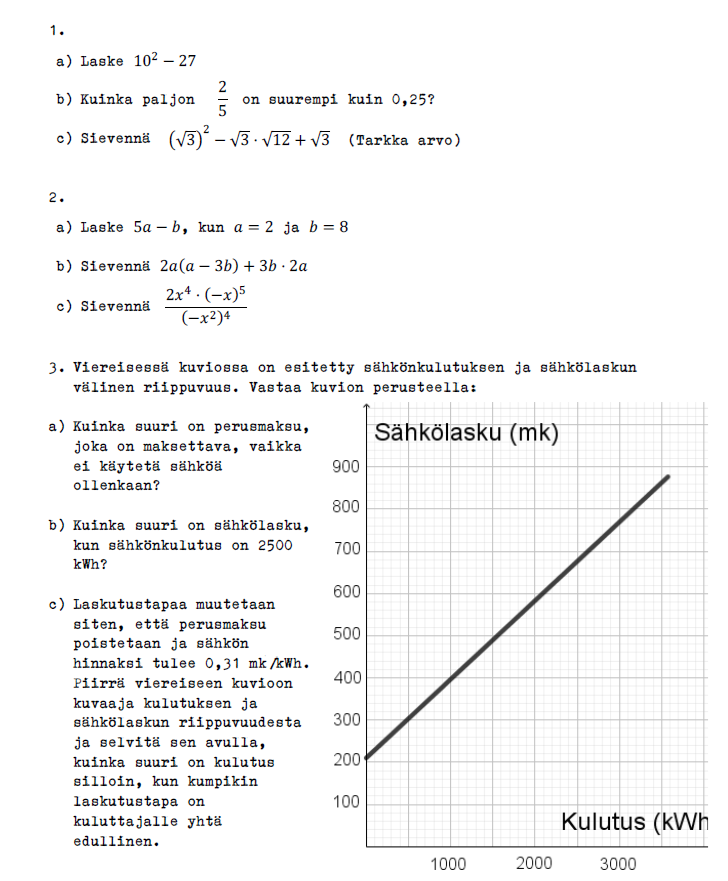
Toisen tehtävän a- ja b-kohdat ovat hyvin tyypillisiä myös 2020-luvun koulumatematiikassa, ja tällaisia yksinkertaisia polynomitehtäviä oppilaat pääsevät ratkomaan myös tämän päivän valtakunnallisissa kokeissa. Kohdan c vaikeustaso ei sekään ole sitä luokkaa, etteikö tehtävää voisi panna kirjainlaskennan kokeeseen. Tällä hetkellä voimassa olevat päättöarvioinnin kriteerit lausuvat melko vähän siitä, minkä tasoisesti kirjainlausekkeita pitää osata sieventää korkeimpia arvosanoja ajatellen.
Jotkut tehtävät kestävät aikaa erinomaisesti. Kolmostehtävä on tällainen. Kun markkojen tilalle vaihdettaisiin eurot, hinnat olisivat jopa melko lähellä viime vuosien todellisuutta – toki kalliin puoleiset sentään. Tehtävä on sekä formaatiltaan että vaatimustasoltaan täysin ajankohtainen, ja tehtävän sisällä eriytyvän vaikeustason mukaisesti osuu melko hyvin nykyisten päättöarvosanan kriteerien 5, 7 ja 9 tasolle kohta kohdalta edeten.
Keskiosan tehtävät: tuttua ja vierasta
Neljäs tehtävä jättäisi nykyiset yläkoululaiset melko lailla vaille mahdollisuuksia. Edes alkeellinen murtolausekkeiden käsittely ei kuulu enää millään muotoa opetettaviin sisältöihin. Lausekkeiden käsittelyn taitoa pidettiin tasokurssien päättymisen jälkeen yllä monissa kouluissa matematiikan valinnaiskursseilla ainakin 2000-luvun ensimmäiselle vuosikymmenelle saakka, mutta nykyään näitä järjestetään enää harvoissa kouluissa. Tottumattomuus polynomien ja rationaalilausekkeiden ”pyörittelyyn” aiheuttaa käsittääkseni monille hankaluuksia etenkin lukion pitkässä matematiikassa, jossa muistikaavat ja lausekkeiden käsittely pitäisi edelleen ottaa haltuun melko nopeasti.
Sen sijaan viidennen tehtävän a- ja b-kohdat pitäisi olla monella peruskoululaisella hallussa tänäkin päivänä, joskin nimittäjien poistoa vaativia hankalampia yhtälöitä esiintyy nykyisissä valtakunnallisissa kokeissa harvakseltaan. Tehtävän viimeinen kohta on tekstimäärältään mittava ja epäilemättä saisi nykyiseen kokeeseen pantuna aikaiseksi palautteita siitä, soveltuvatko pitkät tehtävänantotekstit matematiikan kokeeseen. Erinomainen mittari se silti olisi yhä: sekä luetun ymmärtämiselle että matemaattisen työkalupakin hyödyntämisen taidolle.

Seuraava eli kuudes tehtävä voisi sellaisenaankin esiintyä nykyisessä polynomilaskennan kokeessa. Valtakunnallisissa kokeissa nykyisen opetussuunnitelman aikana polynomeista on ollut pääasiassa vain perustehtäviä, ja geometriaan linkittyviä kirjainlaskennan tehtäviä on esiintynyt harvakseltaan. Pinta-alan selvittämiseen vaadittava polynomien kertolasku ehtii monelta unohtua 9. luokan kevääseen mennessä, ellei sopivaa kertaushetkeä satu kohdalle. Näkemissäni 80-luvun oppikirjoissa spiraaliperiaate toteutuu melko vahvasti, ja polynomiasiaakin kerrataan ja syvennetään vuodesta toiseen.
Seitsemännessä tehtävässä kuvattu tilanne lihatiskillä asioinnista oli varmaankin jokaiselle koululaiselle tuttu 80-luvun Suomessa, mutta miten mahtaisi olla tänä päivänä? Ellei tehtävän konteksti pääse häiritsemään, moni pääsisi pisteille tänäkin päivänä. Tosin kilohinnan laskeminen on osoittautunut viime vuosina yllättäväksi haasteeksi monille yläkoulun aloittaneille. Kohdissa b ja c esiintyvät keskitasoinen ja vaikeahko prosenttilaskutehtävä ovat melko tuttuja näkyjä myös nykypäivän valtakunnallisissa kokeissa.
Viimeiset tehtävät: kuka muistaa geometrian kaavat ulkoa?
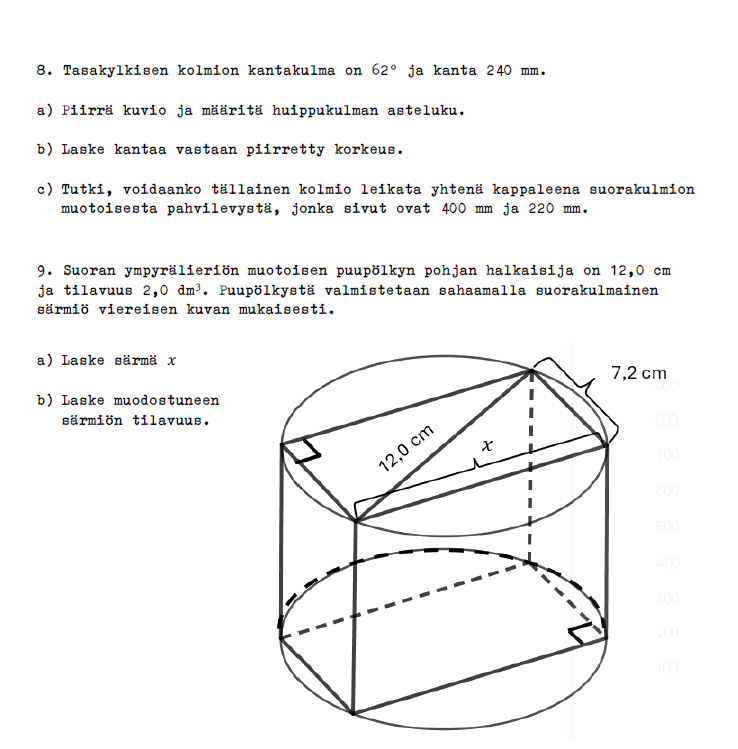
Kokeen lopussa on kaksi melko haastavaa geometrian tehtävää. Syystä tai toisesta nykyisissä oppikirjoissa lähes kaikkiin trigonometrian tehtäviin tarjotaan valmis mallikuva, vaikka kahdeksannen tehtävän mukainen tilanne olisi paljon opettavaisempi. Sinänsä tehtävässä ei c-kohtaa lukuun ottamatta ole mitään tämän päivän vaatimustason ylittävää, ja saattavat nykyistenkin valtakunnallisten kokeiden viimeiset geometrian tehtävät olla varsin haastavia. Huomionarvoista on toki se, ettei vuoden 1985 kokeen ohjeistus sisällä tietoa oppilaille annettavista kaavoista, joten taso- ja avaruusgeometrian peruskaavat on pitänyt kaiketi opetella ulkoa. Tämä lisää etenkin jo muutoinkin melko vaikean yhdeksännen tehtävän vaikeustasoa.
Yhteenvetoa ja pohdintaa
Jonkinlaisena yhteenvetona voisi todeta, ettei vuoden 1985 kokeen yksittäisten tehtävien vaikeustaso ole sinänsä ylivoimainen tähän päivään verrattuna. Ennen mukavaan oloon tuudittautumista on kuitenkin huomioitava useampi seikka. Ensinnäkin nykyiset valtakunnalliset kokeet sisältävät geometrian kaavat sekä kohtalaisen joukon tehtäviä ja alakohtia, jotka ovat helpompia kuin mikään vuoden 1985 kokeen tehtävä. Ja sittenkin menestys valtakunnallisessa kokeessa on vuotuisten pisteyhteenvetojen mukaan nykyään heikonlaista – viime kevään pistekeskiarvo oli 28/70 ja arvosanana 6+. Vuoden 1985 kokeessa pistekeskiarvo oli 23:n ja 24:n välissä (arvosanakeskiarvo 6,8), mutta maksimipistemäärä olikin tuolloin vain 48. Lyhyesti ja vähän tylystikin voidaan sanoa, että kokeet ovat helpottuneet, ja niissä menestytään aiempaa huonommin. Toki joku saattaisi oikeutetusti huomauttaa, että myös sisällöt ovat muuttuneet ja nykyään opiskellaan asioita, joihin ei vielä 80-luvulla peruskoulussa paneuduttu. Mieleen tulevat lähinnä tilastoihin ja todennäköisyyteen liittyvät sisällöt sekä ohjelmointi, johon liittyvän osaamisen mittaaminen on oma haasteensa.
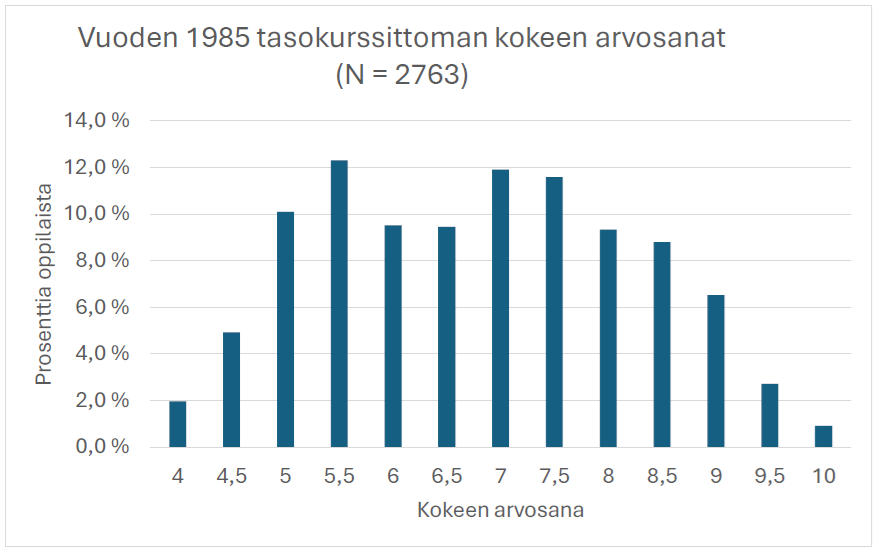
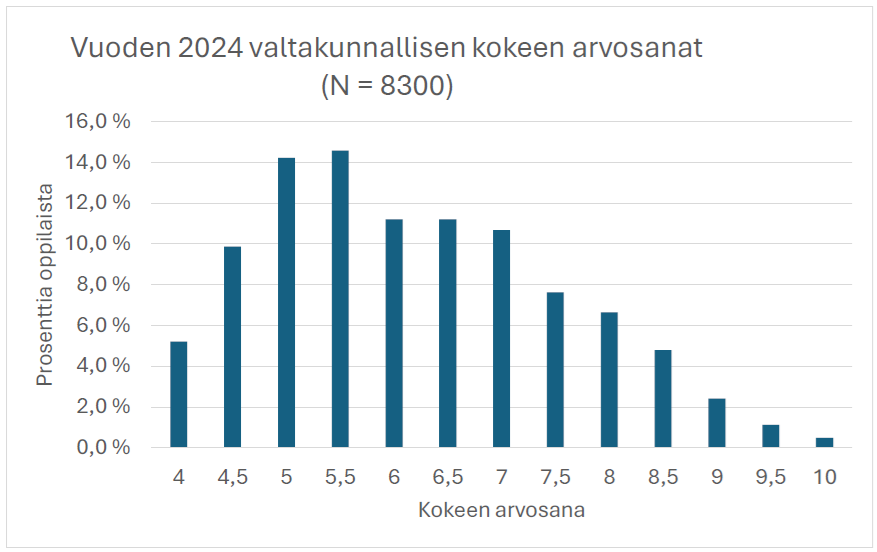
Alla olevat tulosjakaumat vuodelta 1985 sekä viime keväältä kertovat oman tarinansa. MAOL:n vuoteen 1985 asti ilmestyneestä Relaatio-lehdestä saamani tulokset 39 vuoden takaa muodostavat lievästi kaksikyttyräisen mutta sittenkin symmetrisen jakauman. MFKA-Kustannus Oy:n julkaisema viime kevään (2024) jakauma, josta olen laskenut arvosanoja saaneiden prosenttiosuudet niin ikään puolen numeron välein, on oikealle vino. Kaiken lisäksi nykyään käytössä oleva arvosanataulukko antaa jakauman alapäässä hieman parempia arvosanoja kuin vuoden 1985 vastaava taulukko, joten tuon ajan suhteellisilla pisterajoilla etenkin arvosanoja 4 ja 4,5 esiintyisi vielä runsaammin vuoden 2024 tulosjakaumassa.
Pitäisin erittäin mielenkiintoisena kokeilua, jossa jotkut koulut tai vähintäänkin luokat suorittaisivat valvotusti jonkin 80-luvun tasokurssittoman matematiikan kokeen. Kokeesta voitaisiin karsia pois murtolausekkeisiin liittyvät tehtävät, koska niiden opettaminen ei enää kuulu opetussuunnitelmaan. Sen sijaan enemmän tai vähemmän kaikki muu kuuluu, ja olisi paikallaan tutkia, miten vanhan vaatimustason kanssa kävisi.
Loppubonus: mitä laajalla tasokurssilla opiskeltiin?
Ikään kuin loppubonuksena esittelen vielä vuoden 1985 valtakunnallisen kokeen laajalle kurssille tarkoitetun version. Sen voisi antaa nykyään tehtäväksi esimerkiksi sellaiselle matematiikan opetuksen erikoisluokalle, jolla on muita perusopetuksen ryhmiä enemmän aikaa ja mahdollisuuksia laajentaa ja syventää yläkoulun oppimäärää. Jo tehtävien silmämääräinen vilkaisu riittää osoittamaan yhden huonon puolen siitä ratkaisusta, että tasokursseista luovuttiin. Nykyisen yläkoulumatematiikan opiskelulla on hyvin vaikeaa tai jopa mahdotonta saavuttaa sitä osaamistasoa, jonka merkittävän suuri osa ikäluokasta, vaikkakin toki vähemmistö, saavutti laajan tasokurssin opiskelemalla. Vaikka mahdollisuus tasokursseihin onkin kenties menetetty iäksi, riittävän vaatimustason ja ylöspäin eriyttämisen vaaliminen on kriittisen tärkeää. Muutoin voi käydä niin, että kymmenen vuoden kuluttua tämän tyyppinen vertailu osoittaa yläkoulumatematiikan lähestyvän sisällöiltään ja vaatimuksiltaan entisaikojen suppeaa yleiskurssia, mikä tuskin oli tasokurssien poistossa asetettu tavoite.
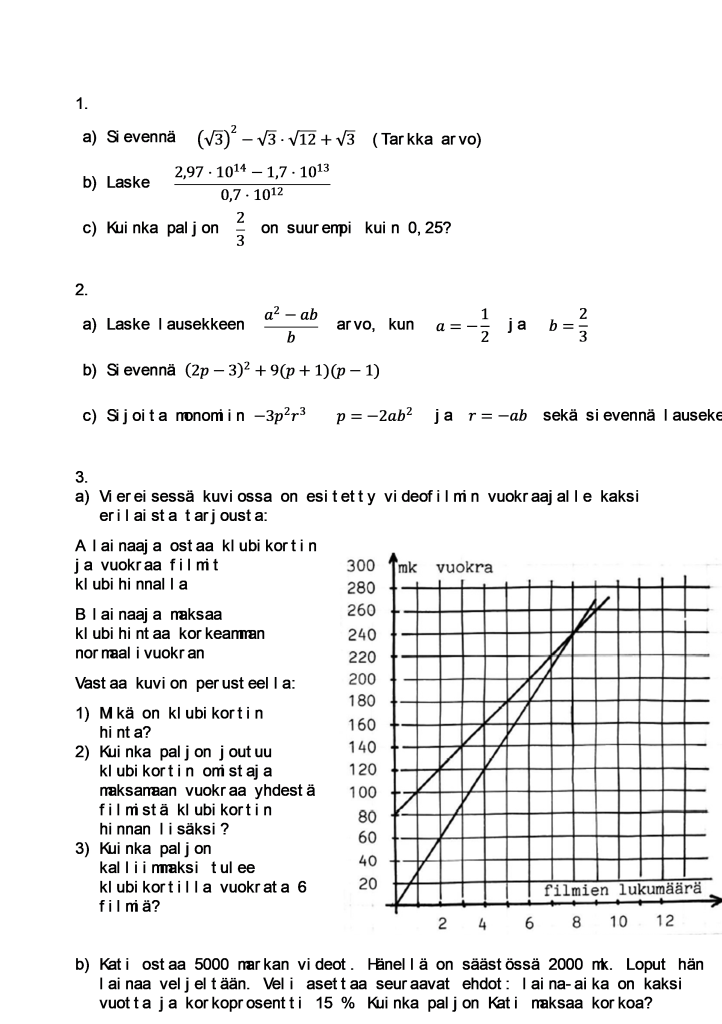
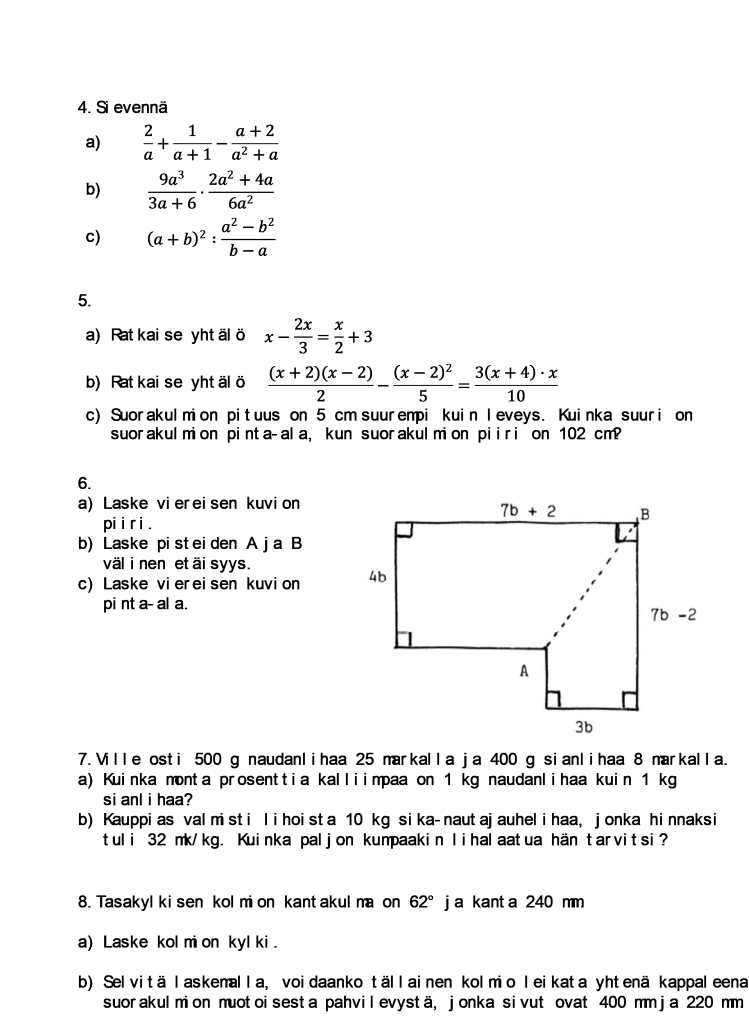
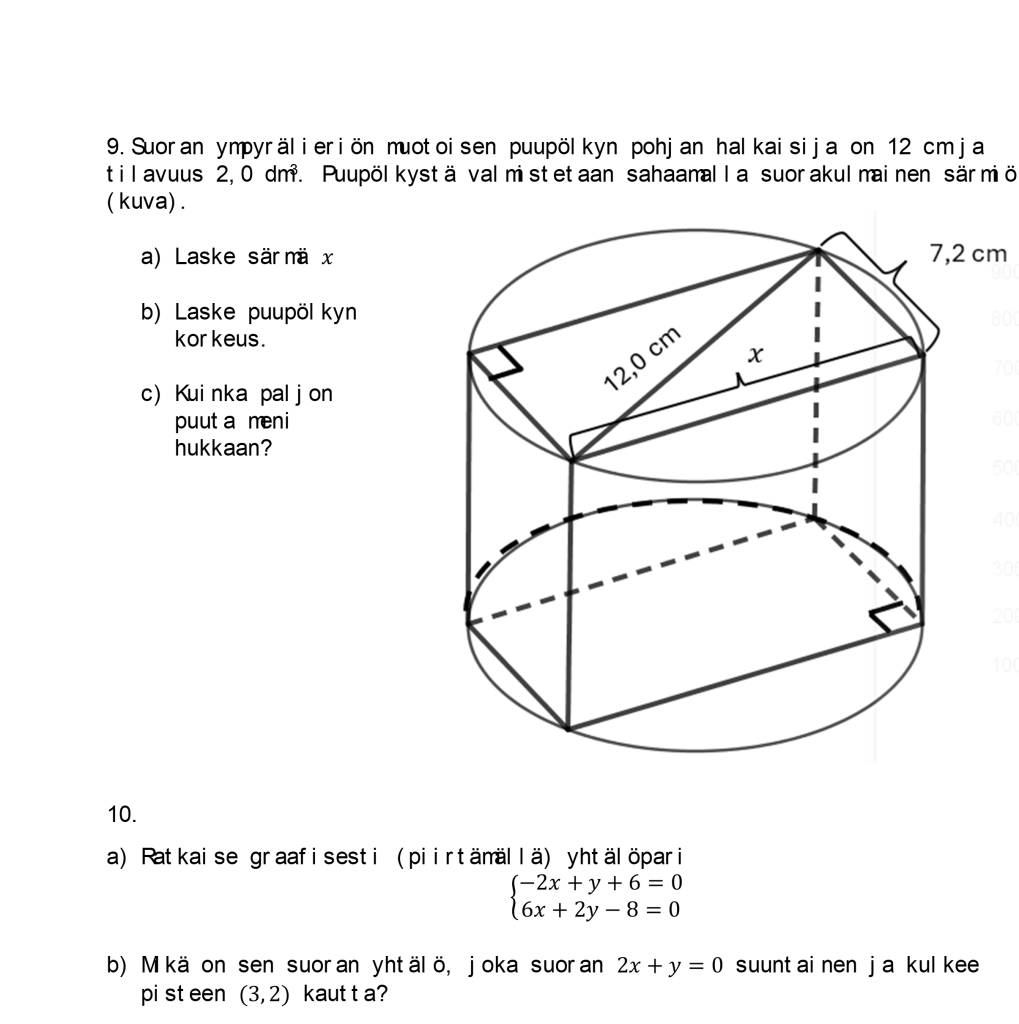
Kuva 6. Vuoden 1985 laajan matematiikan koe.
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista







