Monikulmioiden jakamisia

Matematiikan mahtavimpia piirteitä on ideoiden yleistettävyys. Yksinkertainen ongelma laajenee vähittäisillä muunteluilla laajaksi ongelmakentäksi tai kokonaiseksi teoriaksi. Tässä jutussa tarkastellaan monikulmion jakamista osiin.

Lähtökohta on Ville Aitlahden matikkamatskujen videossa [1].  Neliö jaetaan neljäksi nelikulmioksi, joissa kahtena sivuna ovat neliön sivun puolikkaat ja joiden kaikkien yhteinen kärkipiste on neliön sisällä oleva piste (kuva 1). Videon pääsisältö on sen todistaminen, että vastakkaisten nelikulmioiden pinta-alojen summa on puolet neliön pinta-alasta.

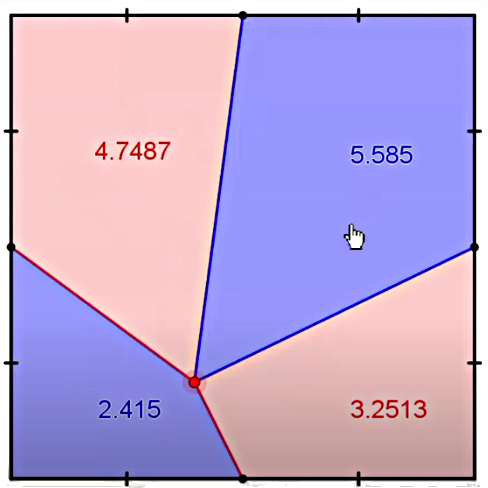
Olkoon ensimmäisenä muunnelmana se, että neliön sivuilla olevat jako-osien kärkipisteet eivät ole neliön sivujen keskipisteitä, vaan määräsuhteeseen jaettujen sivujen jakopisteitä [2]. Sama vastakkaisten nelikulmioiden summien yhtäsuuruus pätee edelleen (kuva 2).

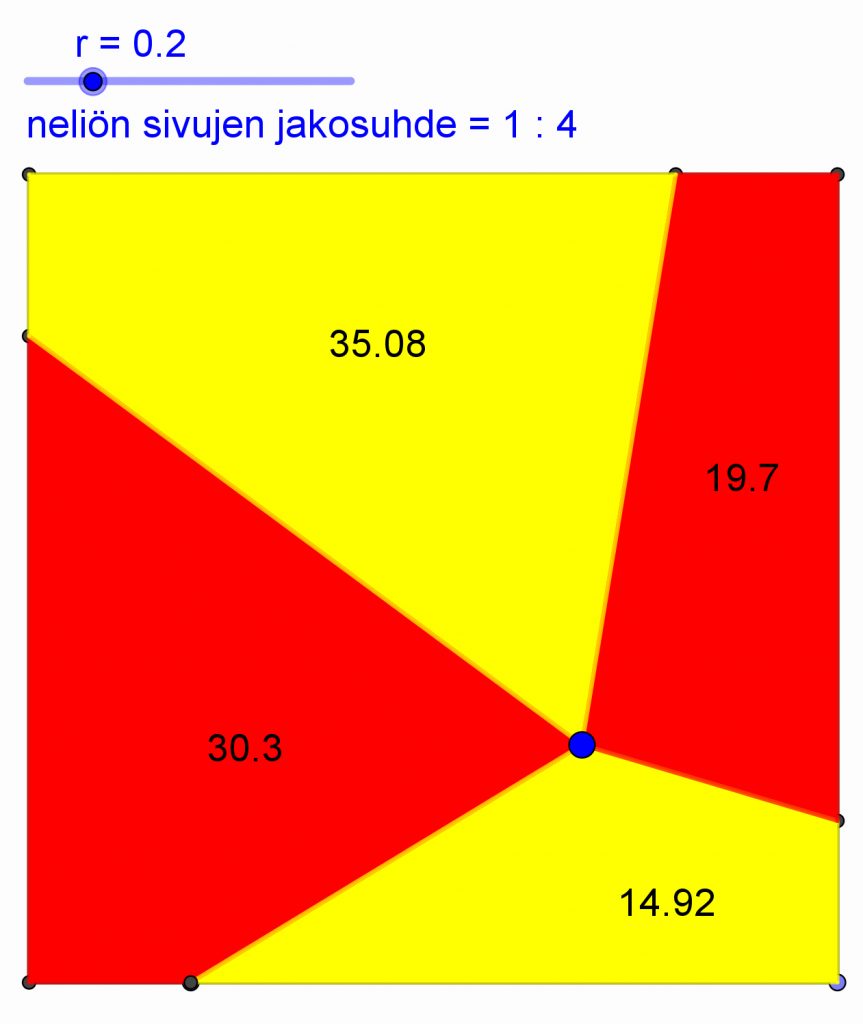
Säännöllinen monikulmio voidaan jakaa vastakkaisiksi nelikulmioiksi vastaavalla tavalla [3] aina, kun sivujen määrä on parillinen (kuva 3). Vastakkaisten, kuvassa samanväristen nelikulmioiden pinta-alojen summat ovat yhtä suuret. Samalla periaatteella voi jatkaa muihin säännöllisiin monikulmioihin.

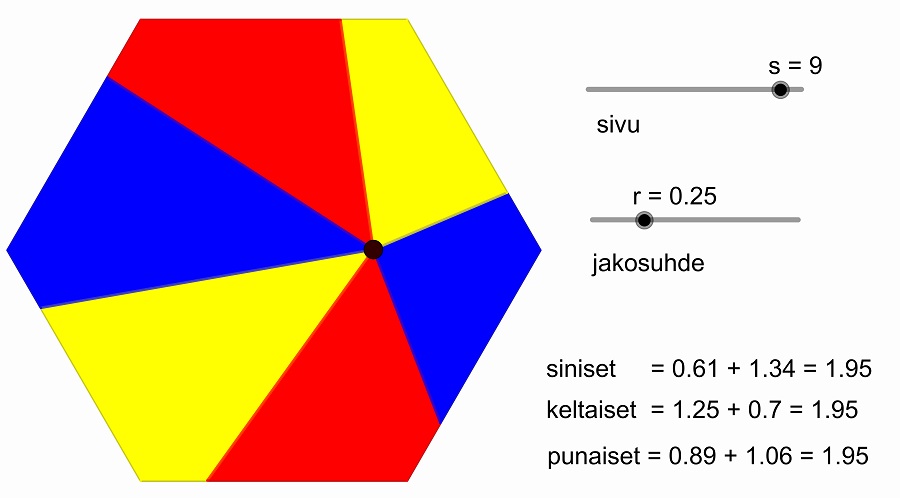
Säännöllisen monikulmion jakaminen yhtä suuriksi osiksi edellä mainitulla tavalla ei ole mahdollista, kun sivujen määrä on pariton. Paritonsivuinen säännöllinen monikulmio voidaan kuitenkin jakaa yhtä suuriksi osiksi [4], joiden yhteinen kärkipiste on kuvion keskipisteessä (kuva 4). Tämän tapainen periaate näyttää sopivan kaikille säännöllisille monikulmioille [5] (kuva 5).

Monikulmioiden tasanjaosta (engl. equidissection) on viimeisen puolivuosisadan aikana kasvanut ihan oma matematiikan tutkimusalueensa. On esimerkiksi osoitettu, että ei neliötä eikä useimpia muitakaan monikulmioita voi jakaa tasan parittomaksi määräksi yhtä suuria kolmioita [6]. Jako parilliseksi määräksi kolmioita kyllä onnistuu useallakin tavalla (kuva 6).

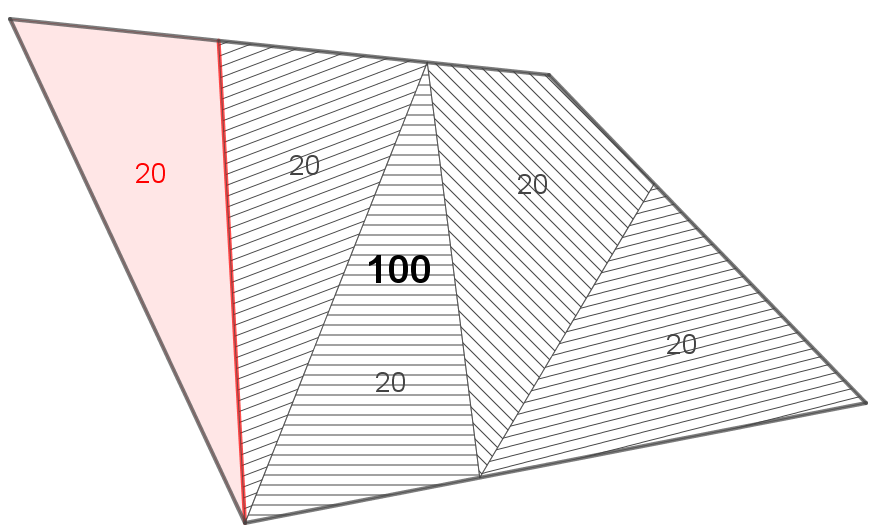
Myös epäsäännöllisiä monikulmioita voidaan jakaa yhtä suuriksi osiksi. Menetelmä [7] on rekursiivinen ja työläs. Se perustuu siihen, että erotetaan ensin esimerkiksi nelikulmiosta viidesosa (kuva 7) tiettyjen sääntöjen mukaan. Sitten erotetaan jäljelle jääneestä nelikulmiosta vastaavalla tavalla neljäsosa jne.

Lähteet:

[1] Aitlahden video https://www.youtube.com/watch?v=iF5G6uH75rA

[2] Geogebra-materiaali https://www.geogebra.org/m/hfc7ccjm

[3] Geogebra-materiaali https://www.geogebra.org/m/rzrcfkkr

[4] Tal, I. Geogebra-materiaali https://www.geogebra.org/m/pHajWs2u

[5] Geogebra-materiaali https://www.geogebra.org/m/enubwxt9

[6] Equidissection https://en.wikipedia.org/wiki/Equidissection

[7] Khetarpal, S. Dividing A Polygon In Any Given Number Of Equal Areas osoitteessa http://www.khetarpal.org/polygon-splitting/