Oloinaccin lukujono
Lukuteoria keskittyy lukujen tutkimukseen. Perinteisesti kyseessä ovat luonnolliset luvut. Niin on tässäkin kehittämäni lukujoukon tapauksessa.
Johdanto
Ajatuksen Oloinaccin lukujonosta sain kun tutkin Fibonaccin lukuja. Fibonaccin lukujonohan on lukujono joka saadaan kun lasketaan aina yhteen kaksi edellistä lukua ja muodostetaan näin uusi luku. Fibonaccin lukujonon ensimmäiset kymmenen lukua järjestyksessä ovat 0, 1, 1, 2, 3, 5, 8, 13, 21 ja 34.
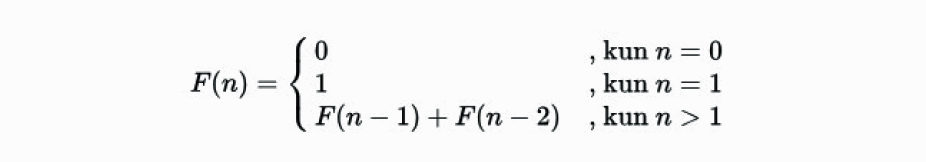
Fibonaccin luvuista on muokattu useita eri muotoja. Tribonaccin luvuissa lasketaan kahden sijaan yhteen kolme perättäistä lukua. Sen ensimmäiset luvut ovat 0, 0, 1, 1, 2, 4, 7, 13, 24 ja 44.
Tribonaccin lukuja seuraavat korkeamman asteen lukujonot ovat Tetranacci, Pentanacci, Heksanacci, Heptanacci, Octanacci ja Enneanacci. Näissä lasketaan neljä, viisi, kuusi, seitsemän, kahdeksan tai yhdeksän perättäistä lukua yhteen.
Oloinaccin lukujono
Oloinaccin lukujonossa luvun arvo saadaan kun lasketaan yhteen lukujonon kaikki edelliset luvut. Tästä tuleekin nimitys. Kreikankielen sana όλοι on suomeksi kaikki. Yhdistin sen vain Fibonacci-sanaan. Siis Oloinaccin luvut.
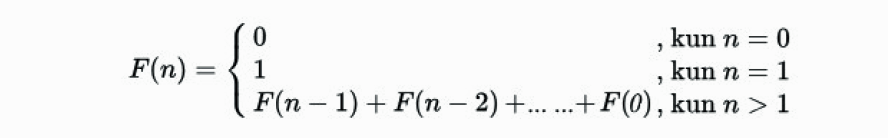
Tietty Oloinaccin luku saadaan laskettua myös yksinkertaisella kaavalla:
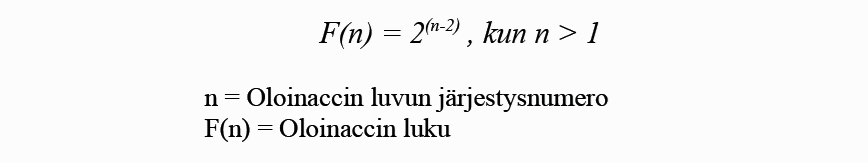
Ensimmäset kymmenen Oloinaccin lukua ovat 0, 1, 1, 2, 4, 8, 16, 32, 64 ja 128.
Oloinaccin luvuilla on paljon mielenkiintoisia ominaisuuksia ja olen määrittänyt niistä muutamia konjektuureja.
Konjektuuri 1 (jaollisuus):
Kun n > 2, ovat kaikki Oloinaccin luvut jaollisia kahdella. Mistä seuraa että seuraavan Oloinaccin luvun saa kertomalla Oloinaccin luvun kahdella.
Konjektuuri 2 (loppusekvenssi):
Kun n > 2, noudattavat Oloinaccin lukujen viimeiset numerot sekvenssiä 2, 4, 8, 6, 2, 4, 8, 6. 2, 4….
Konjektuuri 3 (numerosuhde):
Kun Oloinaccin luvun numeroiden määrä N jaetaan Oloinaccin luvun järjestysnumerolla n saadaan aina tulokseksi likimäärin 0,3. Kuitenkin kun Oloinaccin luvun järjestysnumero on tasakymmen saadaan aina täsmälleen 0,3.
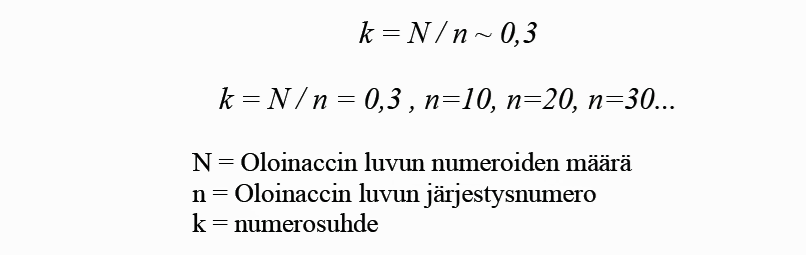
Konjektuuri 4 (korotus):
Kun Oloinaccin luku korotetaan toiseen potenssiin saadaan aina tulokseksi jokin Oloinaccin luku.
Lopuksi
Mielenkiintoistahan näitä on pohtia. Ja tulokset saattavat olla joskus todella yllättäviäkin.
