Otavan havainnollistuksia GeoGebralla

Otava on tunnetuimpia pohjoisen tähtitaivaan kuvioita. Siitä kerrotaan sekä kansanrunoudessa että tähtitieteen kirjoissa ja verkkosivuilla. Tekstit ja taulukkotiedot alkavat elää dynaamisissa malleissa.

Otava on osa Suuren Karhun tähdistöä. Suomenkielisen nimensä se on saanut virtapaikoissa käytetystä kalaverkosta. Muualla maailmassa se on nähty muun muassa aurana, kauhana tai vaunuina.

Otavan tähtikuvio koostuu seitsemästä tähdestä. Niillä on arabialaisperäiset nimet (kuva 1). Nimet eivät ole vakiintuneita, vaan käytössä on useita kirjoitusmuotoja, jopa eri nimiä, esimerkiksi Alkaidista myös nimeä Benetnasch [1]. Nimeämisperusteet eivät useinkaan ole enää tiedossa. Esimerkiksi Alkaidin sanotaan saaneen nimensä ruumissaaton itkijänaisen mukaan.

Kansainvälinen tähtiteellinen unioni on julkaissut yhtenäistävän nimilistan vain muutama vuosi sitten [2]. Siinä käytetään nimen ohella nimeävää merkintää, joka kertoo mihin tähdistöön tähden katsotaan sijoittuvan. Koska Otava kuuluu Ison Karhun tähtikuvioon (Ursa Major), niin esimerkiksi Dubhe on α Ursae Majoris (α UMa) ja Merak on β Ursae Majoris (β UMa). Tässä luettelossa Otavan tähdet on merkitty kreikkalaisin aakkosin α:sta η:aan tähtikuvion mukaisessa järjestyksessä, vaikka varsinkin aikaisemmin kreikkalaisia aakkosia on käytetty kirkkauden mukaisessa järjestyksessä niin, että tähtikuvion kirkkainta tähteä on merkitty α:lla jne.

Viisi Otavan tähdistä on suunnilleen samalla noin 80 valovuoden etäisyydellä Maasta, Alkaid ja Dubhe vähän kauempana. Kirkkain on Alioth (näennäinen kirkkaus 1,77), himmein Megrez (3,31). Mizar on kaksoistähti, mutta osat eivät erotu paljaalla silmällä. Hyvin lähellä Mizaria on himmeämpi tähti Alcor, jota on käytetty näkökyvyn testinä. [3]

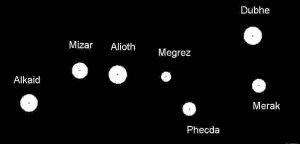
Tähtitaivas samoin kuin tähtikartta näyttävät tähtikuvion kaksiulotteisena (kuva 2, vasen). Todellisuudessa tähtikuvio on kolmiulotteinen, sillä tähdet ovat eri etäisyyksillä Maasta. Havaitsijan sijainnista riippumaton pallokoordinaatisto (kuva 2, oikea) on ekvatoriaalinen koordinaatisto. Sen xy-taso (ekvatoriaalitaso) on Maan päiväntasaajataso ja z-akseli sama kuin Maan akseli.

Pituuspiiriä vastaava koordinaatti rektaskensio θ ilmoittaa kohteen suunnan kulmaetäisyyden kevättasauspisteestä vastapäivään mitattuna (samoin kuin itäinen pituus maapallolla, meridiaani, pituuspiiri). Se ilmoitetaan tunteina, minuutteina ja sekunteina. Tämä kuulostaa ehkä vaikealta, mutta on käytännöllistä, koska näin rektaskensio kertoo, milloin kohde on etelässä eli korkeimmillaan taivaalla.  

Deklinaatio ϕ ilmoittaa tähden kulmakorkeuden horisontista (samoin kuin pohjoinen leveys, latitudi, leveyspiiri). Se ilmoitetaan asteina, minuutteina ja sekunteina välillä [0, 90°]. Tämän kanssa pitää olla tarkkana, sillä pallokoordinaatistoissa käytetään usein toisena kulmakoordinaattina myös ϕ:n komplementtikulmaa [5]. Katso lisätietoa täältä [6].

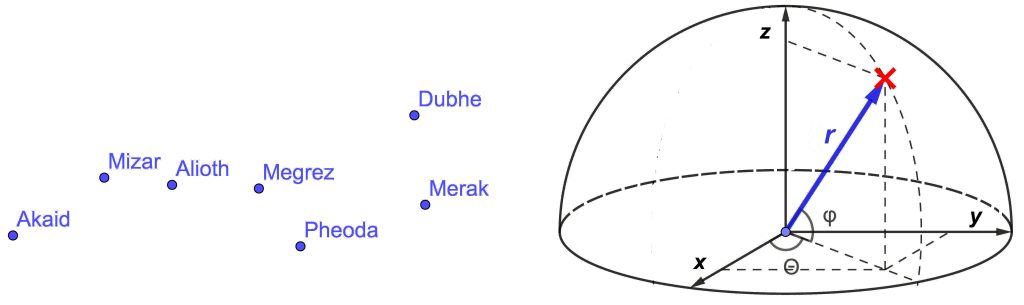
Taulukko: perustietoja Otavan tähdistä (lähteen [3] mukaan)

IAU:n tunnus	Bayerin luettelon merkintä	Nimi	rektaskensio (engl. right ascension)	deklinaatio	näen- näinen kirkkaus	todellinen kirkkaus	etäisyys Maasta (valovuosia)
α UMa	α	Dubhe	11h 03m 43.84s	+61° 45′ 04.0″	1.79 (β)	−1.08	124
β UMa	β	Merak	11h 01m 50.39s	+56° 22′ 56.4″	2.37 (ε)	0.41	79
γ UMa	γ	Phecda	11h 53m 49.74s	+53° 41′ 41.0″	2.44 (ζ)	0.36	84
δ UMa	δ	Megrez	12h 15m 25.45s	+57° 01′ 57.4″	3.31 (η)	1.33	81
ε UMa	ε	Alioth	12h 54m 01.63s	+55° 57′ 35.4″	1.77 (α)	−0.21	81
Mizar	ζ	Mizar	13h 23m 56s	+54° 55′ 25″	2,04 (δ)	0.25	83
η UMa	η	Alkaid	13h 47m 32.55s	+49° 18′ 47.9″	1.86 (γ)	-0,60	101

Kolmiulotteinen kuva voidaan piirtää esimerkiksi 3D-Geogebralla. Se ei lue taulukon koordinaattilausekkeita sellaisinaan. Ne saadaan ymmärrettävään muotoon helposti vaikkapa Excelillä. Esimerkiksi Dubhen rektaskensio asteina on 360 · (11 + 6 / 60 + 43,84 / 3600) / 24 ≈ 165,93. Kuva näyttää sellaiselta kuin pitääkin, vaikka kolmiulotteisuuden hyöty ei näy, kun katsotaan pelkkiä tähtiä (kuva 3, vasen). Kolmiulotteisuus näkyy kuitenkin jo tähtien keskinäisistä etäisyyksistä (kuva 3, oikea).

Kolmiulotteista kuvaa [8] voi kiertää ja tarkastella siten Otavan muotoa muualta kuin Maasta katsottuna ja samalla Maan ja Otavan tähtien keskinäistä sijaintia eri suunnista nähtynä (kuva 4). Keskinäiset etäisyydet säilyvät tietysti kierrossa, mutta Otava näyttää toisenlaiselta kuin Maasta katsottuna.

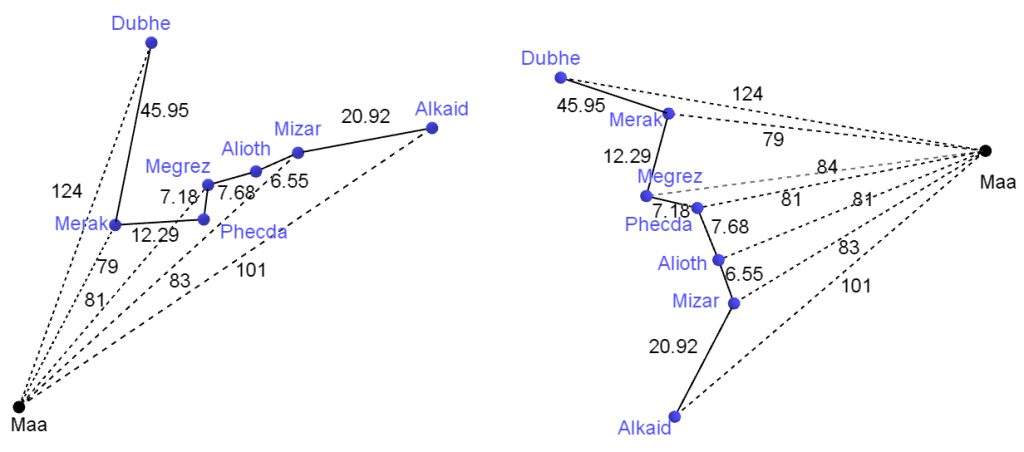
Geogebra tekee tämän kuvan piirtämisen helpoksi, sillä se tulkitsee puolipisteillä erotetut koordinaatit pallokoordinaateiksi, esimerkiksi (100; 45°; 60°). Kaukana origosta, edellä siis Maasta, olevat pisteet saadaan näkymään, kun kuvaa skaalataan hiiren vierityspyörällä.

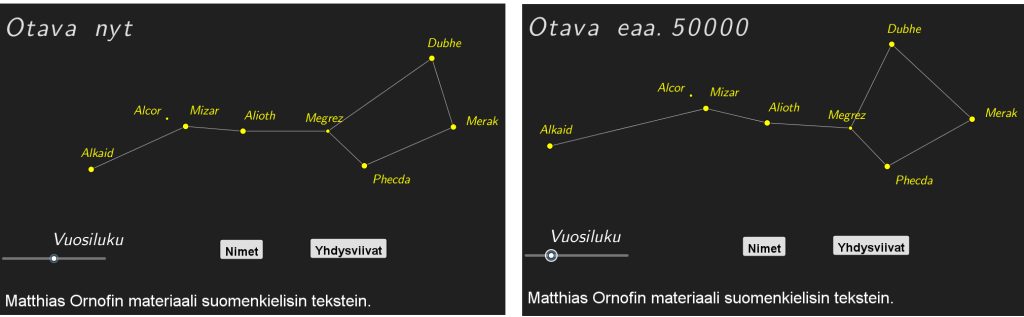
Otavan tähtikuvion muoto muuttuu ajan mukana, sillä tähdet liikkuvat eri suuntiin (kuva 5).

Lisää luettavaa ja tutkittavaa

[1] Tähden nimi osoitteessa [2] List of proper names of stars osoitteessa https://en.wikipedia.org/wiki/List_of_proper_names_of_stars

[3] List of stars in Ursa Major osoitteessa https://en.wikipedia.org/wiki/List_of_stars_in_Ursa_Major

[4] Geogebra-materiaali Otavan tähtien näennäiset kirkkaudet osoitteessa https://www.geogebra.org/m/esrhdq6n

[5] Geogebra-materiaali Brezinski, Tim: Spherical Coordinates: Dynamic Illustrator osoitteessa https://www.geogebra.org/m/h9xS5ZZs

[6] Lisätietoja atikkelista Korhonen, Hannu: Pallogeometrian perushahmotusta, osa 5, Dimensio 5.6.2019 https://dimensiolehti.fi/pallogeometrian-perushahmotusta-osa-5/

[7] Otava osoitteessa https://www.astro.utu.fi/zubi/constel/dipper.htm

[8] Geogebra-materiaali Otavan ja Maan muodostama järjestelmä2 osoitteessa https://www.geogebra.org/m/by9bpxk3

[9] Geogebra-materiaali Hornof, Matthias:  Ursa Major osoitteessa https://www.geogebra.org/m/BYc8x5cA