Pythagoraan porsaat

Pythagoraan lause on ollut ja on edelleen olennainen osa koulumatematiikkaa. Siitä saataisiin kuitenkin irti paljon enemmän kuin tavanomaiset oppikirjat tarjoavat.

Pythagoraan lause on nimetty kreikkalaisen filosofin Pythagoraan mukaan, mutta sen asiasisällön tunsivat sekä egyptiläiset että babylonialaiset ja intialaiset jo runsaat tuhat vuotta aikaisemmin [1]. Egyptiläiset käyttivät sitä maanmittauksessa suoran kulman määrittämiseen. Babylonialaiset tunsivat sen numeerisessa muodossa lukukolmikoina. Alkuperäistä savitauludokumenttia säilytetään Columbia Universityn kokoelmissa New Yorkissa [2].

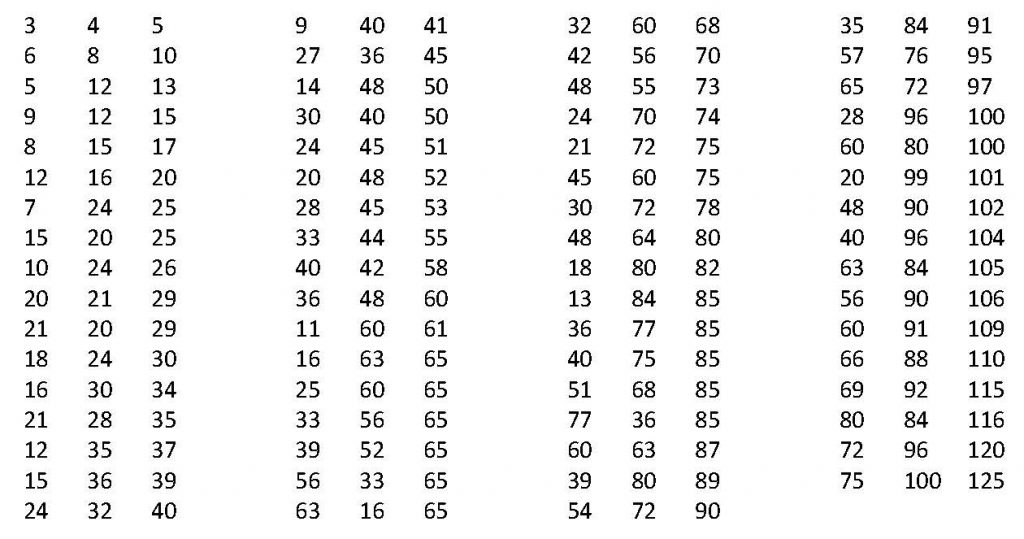
Vielä 150 vuotta sitten Pythagoraan lausetta käsiteltiin koulussa kreikkalaiseen tapaan geometrisessa muodossa, sellaisena se esiintyi myös ylioppilaskirjoitustehtävässä 1874: 2 [3]. Nykyään sitä käytetään enimmäkseen algebrallisessa muodossaan suorakulmaisen kolmion sivujen laskemiseen. On siis tavallaan palattu babylonialaisille juurille, kun etsitään kolmatta ehdon     $a^2+b^2=c^2$ täyttävän lukukolmikon luvuista, kun kaksi muuta tunnetaan. Luonnollisten lukujen joukossa nämä ovat aika harvinaisia, sillä esimerkiksi tällaisia lukukolmikoita, joissa kaksi pienintä lukua ovat pienempiä tai yhtä suuria kuin 100 on vain 67 (taulukko), siis 5000 mahdollisesta lukuparista (taulukko).

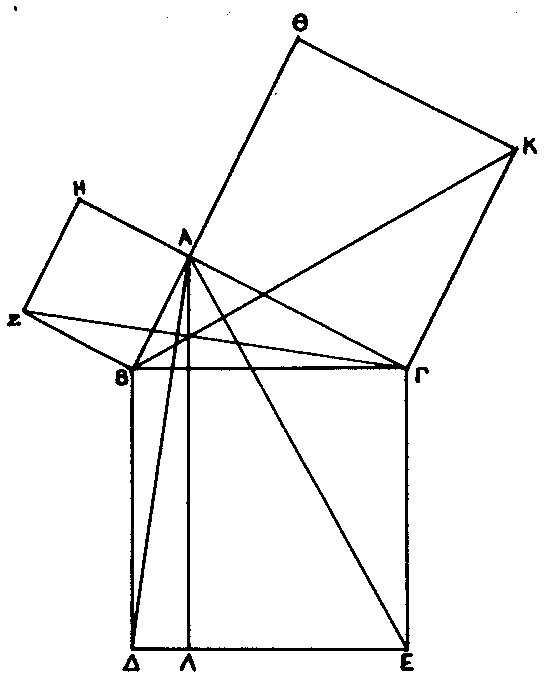
Todistamista varten Pythagoraan lause esitetään koulukirjoissa vieläkin samassa geometrisessa muodossa kuin Eukleideen Alkeissa yli 2000 vuotta sitten (kuva 1) [4]: Suorakulmaisessa kolmiossa suoran kulman vastaiselle sivulle piirretty neliö on yhtä suuri kuin suoran kulman viereisille sivuille piirrettyjen neliöiden summa. Pythagoraan lauseesta on kyllä paljon muuhunkin, vaikka joissakin lähteissä toisin väitetään, siis että ”Pythagorean theorem can only be applied to right triangles.”[5]

Geometrian tarkoituksiin Pythagoraan lause voitaisiin esittää myös näin: Jos suorakulmaisen kolmion sivut ovat a, b ja c ja sen sivuille on piirretty kolme yhdenmuotoista kuviota, siis mittakaavassa a : b : c, niin kahden pienemmän kuvion pinta-alojen summa on yhtä suuri kuin suurimman kuvion pinta-ala. Kuvion ei suinkaan tarvitse olla neliö tai muu monikulmio, vaan mikä tahansa muukin kuvio kelpaa [6], vaikka esimerkiksi porsas [7] (kuva 2).

Kuva 2: Kahden pienemmän porsaan pinta-alojen summa on yhtä suuri kuin suurimman porsaan pinta-ala. Voit muuttaa kolmion muotoa raahaamalla kärkipisteitä.

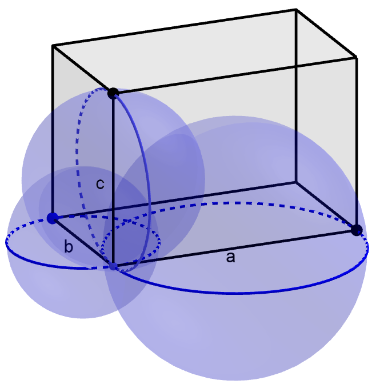
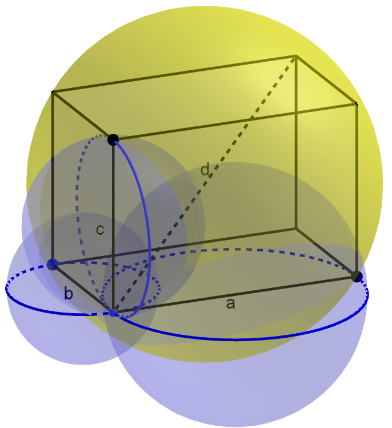
Olisi houkuttelevaa pohtia, yleistyisikö tämä mittakaavatarkastelu myös kolmiulotteisiin kappaleisiin. Tilavuuksien suhdehan on mittakaavan suhdelukujen kolmansien potenssien suhde. Suorakulmaista kolmiota vastaava geometrinen perusta kolmiulotteisessa avaruudessa voisi olla suorakulmainen särmiö, jonka särmät ovat a, b ja c. Piirretään kolme palloa, joiden halkaisijat ovat särmiön toisiaan vastaan kohtisuorassa olevat särmät (kuva 3). Miten tähän kuvaan voisi piirtää pallon, jonka tilavuus olisi näiden kolmen pallon summa? Alkeellisen analogian perustella voisi tutkia palloa, jonka halkaisija on särmiön avaruuslävistäjä (kuva 4 [8]).

Kolmen pallon tilavuuksien summa on     $\frac{4\pi}{3}\left((\frac{a}{2})^3+\left(\frac{b}{2}\right)^3+\left(\frac{c}{2}\right)^3\right)=\frac{\pi}{6}(a^3+b^3+c^3).$ ja neljännen, jonka halkaisija on särmiön avaruuslävistäjä,     $\frac{4\pi}{3}\left((\frac{a}{2})^2+\left(\frac{b}{2}\right)^2+\left(\frac{c}{2}\right)^2\right)^{\frac{3}{2}}=\frac{\pi}{6}\left(a^2+b^2+c^2\right)^{\frac{3}{2}}.$ Neljäs pallo ei siis ole haluamamme, vaikkakin summa lähestyy avaruuslävistäjälle piirretyn pallon tilavuutta, kun kahden muun särmän pituudet lähestyvät nollaa (kuva 5).

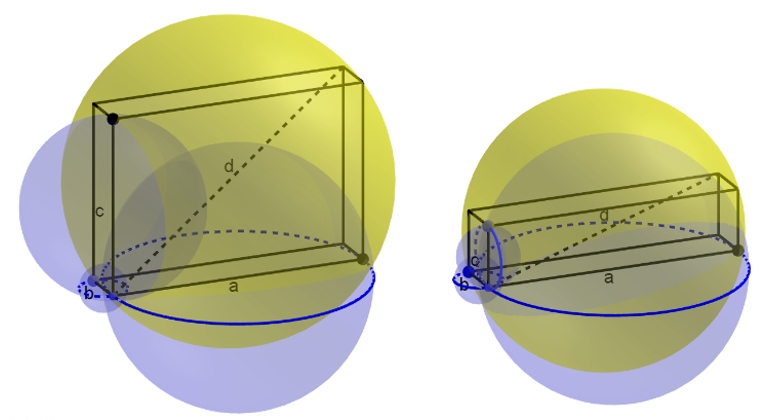
Särmille piirrettyjen pallojen tilavuuksien summan suhde avaruuslävistäjälle piirrettyyn palloon on     $S\left(a,\ b,\ c\right)=\ \frac{a^3+b^3+c^3}{{(a^2+b^2+c^2)}^{3/2}}.$ Helposti nähdään, että tämä lähestyy ykköstä, kun yhtä sivua pidetään vakiona ja kaksi muuta pienenevät kohti nollaa, niin kuin kuvasta 5 jo konkreettisesti nähtiin. Jos yhtä särmää a pidetään vakioparametrina, niin suhde voidaan esittää kahden muun särmän funktiona:     $S\prime\left(a,\ x,\ y\right)=\ \frac{a^3+x^3+y^3}{{(a^2+x^2+y^2)}^{3/2}}.$ Kun x ja y kasvavat rajatta, niin suhde lähestyy lukua     $\frac{1}{\sqrt2}\approx0,707,$ mikä nähdään helposti tavanomaisella rajankäynnillä. 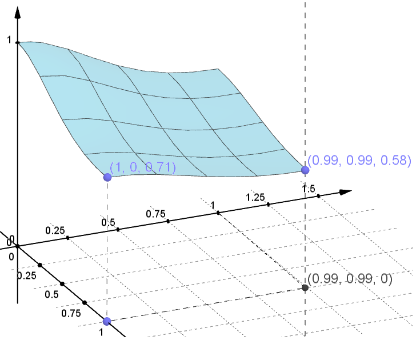Funktion minimiarvo     $\frac{1}{\sqrt3}\approx0,577$ saavutetaan, kun särmiö on kuutio eli siis kohdassa $(a, a)$. Kuvassa 6 on suhdefunktion $S’$ kuvaaja arvolla $a = 1$, kun $0 ≤ x ≤ 1$ ja $0 ≤ y ≤ 1$. Pinnan oikeassa alakulmassa oleva piste vastaa yksikkökuutiota, vasemmassa alakulmassa oleva piste neliötä ja $z$-akselin piste janaksi supistunutta särmiötä.

Lähteitä ja lisää tutkittavaa:

[1] Ifrah, Georges (2001): Räknekonstens kulturhistoria, del 1, s. 148, 227. Wahlström & Widstrand, Smedjebacken.

[2] Plimpton 322 osoitteessa https://en.wikipedia.org/wiki/Plimpton_322

[3] Laurén; Rafaël (1916): Matemaattiset tehtävät ylioppilaskirjoituksissa vuosina 1874–1915, s. 1. Gummerus, Jyväskylä. Katso myös Geogebra-materiaalia A square whose area is equal to the difference of two given squares  https://www.geogebra.org/m/eqtcjcFm

[4] Heath, Thomas L. (1956): The Thirteeen Books of th Elements, vol. 1, Book I, prop. 47, p. 349. Dover Publications, New York.

[5] Pythagorean Theorem Project osoitteessa https://fi.pinterest.com/pin/462252349226241463/

[6] Pythagoras’ Theorem and Areas osoitteessa https://www.mathsisfun.com/geometry/pythagoras-areas.html

[7] Geogebra-materiaali Pythagoraan porsaat osoitteessa https://www.geogebra.org/m/mvwbvsdb

[8] Geogebra-materiaali Suorakulmainen särmiö ja neljä palloa osoitteessa https://www.geogebra.org/m/kexzyc5w