Singapore-matematiikkaa
Singapore on ollut kärjessä vuodesta toiseen TIMSS- ja PISA-tutkimuksissa, jotka mittaavat matematiikan osaamista kansainvälisesti. On syytä hieman tutkia, mitä Singaporessa on tehty toisin. Käsite Singapore-matematiikka on peräisin Yhdysvalloista, kun siellä vertailtiin yhdysvaltalaisten ja singaporelaisten taitoja matematiikassa ja havaittiin suuri ero singaporelaisten eduksi. Monet koulut Yhdysvalloissa ovat alkaneet käyttää Singapore-matematiikan metodeja oppimisessa ja siksi termiä mainostetaan myös oppikirjoissa ja amerikkalaisten koulujen opetussuunnitelmassa.
Aluksi Singaporessa käytettiin oppikirjoja, jotka oli tuotu ulkomailta, onhan Singapore Britannian entinen siirtomaa. 1980-luvulla Singaporen opetushallitus halusi kehittää omia oppikirjoja ja opetussuunnitelmaa, jotka perustuisivat amerikkalaisen psykologi Jerome S. Brunerin julkaisuihin. Hänen lähestymistapansa matematiikkaan on kolmivaiheinen: konkretia (Concrete = C), kuvallinen (Pictoral = P) ja abstrakti (Abstract = A) ja siksi tätä oppimisen metodia usein kutsutaan CPA-metodiksi. Singapore-matematiikka perustuu tähän kolmivaiheeseen metodiin.
Oppimisen kolme vaihetta
Käydään esimerkin avulla läpi CPA-metodia.
1. Konkretia
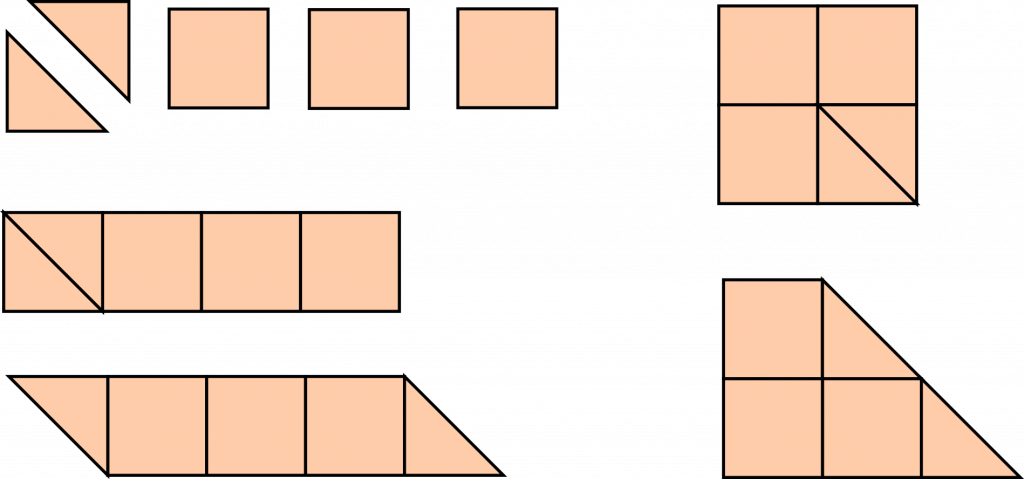
Otetaan käytännön esimerkki geometriasta ja monikulmioista. Aluksi opettaja antaa oppilaille kaksi tasakylkistä kolmiota, jossa huippukulma on suorakulma (Kuva 1). Opettaja pyytää oppilaita tekemään erilaisia kuvioita näillä kahdella kuviolla. Oppilaiden tulokset piirretään taululle. Opettaja kysyy ”mitä yhteistä on kahdella ensimmäisellä kuviolla?” Vastaus: ne ovat nelikulmioita, koska niillä on neljä sivua. Viimeinen kuvio on kolmio, koska sillä on kolme sivua. Lisäksi jokaiselle kuviolle löytyy oma nimi, kuten neliö, suunnikas ja kolmio. Tässä ensimmäisessä vaiheessa luodaan käsitteitä tutkittavista kappaleista. Opettaja kysyy ”Mikä on kuvioiden pinta-ala?” Vastaus: Kaikkien kuvioiden pinta-ala on yksi, koska kuviot ovat palautettavissa neliöksi, joka on pinta-alan perusyksikkö.

Seuraavaksi opettaja antaa kolme neliötä lisää ja pyytää muodostamaan kuvioita, jotka ovat nelikulmiota (Kuva 2). Tulokset piirretään taululle. Sieltä löytyy helposti neljä erilaista vaihtoehtoa, kuten neliö, suorakulmio, suunnikas ja puolisuunnikas. Kun verrataan tuloksia aikaisempiin kuvioihin, niin uutena kuviona löytyi suorakulmio ja puolisuunnikas. Opettaja kysyy: ”Mikä on näiden kuvioiden pinta-ala?” Oppilaat keskustelevat tästä ja tulokset käydään yhdessä läpi. Kaikkien kuvioiden pinta-ala on sama ja se on neljä. Seuraavaksi opettaja pyytää tekemään lisää kuvioita, joiden pinta-ala on 4. Kuviot voivat olla sitten jo mitä tahansa. Vaikka oppilaat välillä tekevät virheitä, niin ne ei tyrmätä, vaan niistä käydään keskustelu. Virheet johtavat uusiin käsitteisiin.
2. Kuvallinen
Seuraavassa vaiheessa otetaan esille ruutupaperi, ja oppilaat piirtävät annetun ohjeen mukaan. Esimerkiksi: piirrä neliöillä ja kolmioilla kaksi kuviota, joilla on sama pinta-ala. Kuvion voit itse päättää. Laske piirtämäsi kuvion pinta-ala. Toisena tehtävänä voisi olla: kuinka monta erilaista kuviota, joiden pinta-ala on kaksi, voit piirtää (Kuva 3), kun käytössä on kaksi kolmiota ja neliö. Kuviot ovat erimuotoisia, kuten kolmio, suorakulmio ja puolisuunnikas.
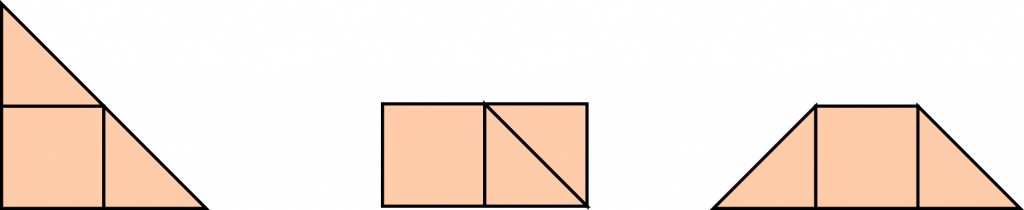
Nyt otetaan myös esille matematiikan tehtäväkirja, jossa ensimmäiset tehtävät ovat kuvallisia tehtäviä. Tehtävänä voi olla esimerkiksi erilaisten pinta-alojen laskemista (Kuva 4) kuviosta.
3. Abstrakti
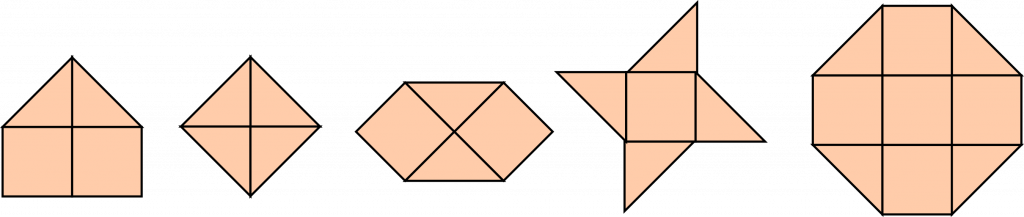
Viimeisessä abstraktissa vaiheessa luodaan laskusääntöjä. Suorakulmion pinta-ala saadaan laskettua myös kertolaskulla, jossa kanta kerrotaan korkeudella. Suunnikkaan pinta-ala lasketaan samalla tavalla kuin suorakulmion pinta-ala, koska suunnikas on helposti muutettavissa suorakulmioksi (Kuva 5).

Kuten tämä esimerkki osoitti, niin Singapore-matematiikassa käytetään paljon aikaa konkretialle ja piirtämiselle. Tärkeää on myös käydä keskustelua oppilaiden kanssa konkreettista havainnosta. Vasta viimeisenä vaiheena on abstaraktin mallin luominen. Periaate Singapore-matematiikassa on, että vähemmän on enemmän. Tärkeää on luoda yhteys konkretian ja abstaraktin mallin välille. Kun yhteys on vahva, niin uuden oppiminen on helpompaa ja jopa hauskaa. Oppiminen perustuu oppilaan omaan oivaltamiseen, ei valmiin mallin antamiseen.
Joustavuus
Toinen erityinen piirre Singapore-matematiikassa on joustavuus. Matematiikassa ei anneta vain yhtä ainoaa ratkaisutapaa, vaan pyritään joustavuuteen. Annetaan oppilaan aluksi itse keksiä oma ratkaisumenetelmä. Otetaan niinkin yksinkertainen esimerkki kuin yhteenlasku. Yhteenlaskulle voidaan esimerkiksi löytää kolme erilaista ratkaisutapaa, joista viimeinen kolmas tapa on Suomessa yleisesti käytetty tapa.
Esimerkki 1: Havainnollistetaan eri tapoja laskea yhteenlasku 48 + 27

Singapore-matematiikassa yleensä päädytään tähän toiseen tapaan, koska se on helpompi havainnollistaa piirtämällä. Allekkainlasku muuttuu silloin seuraavanlaiseksi.
Esimerkki 2: Yhteenlasku allekkain Singapore-matematiikassa
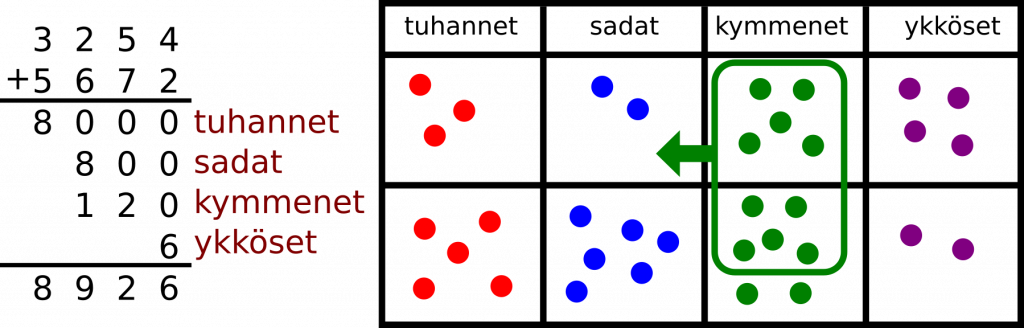
Allekkain laskussa summataan erikseen tuhannet, sadat, kymmenet ja ykköset. Ylitykset eri kymmeniin on helppo havainnollistaa piirtämällä. Suomessa opittu tapa alkaa tuntua paljon hankalammalta, koska Suomen tapa on paljon abstraktimpi. Laskun mekaaninen opettelu ei paranna ymmärrystä. Moni alakoulussa epäselväksi jäänyt asia näkyy helposti oppimisvaikeuksina myös yläkoulussa. Ratkaisu oppimisvaikeuksiin ei ole toiston lisääminen tai laskun helpottaminen, vaan paremminkin konkretian ja piirrosten lisääminen.
Ongelmanratkaisu
Vuoden 1992 Singaporen opetussuunnitelmassa mukaan otettiin ongelmanratkaisutaidot. Ongelman ratkaisumenetelmä perustuu unkarilaissyntyisen matemaatikon George Polyan julkaisuun ”How to Solve it”, jossa ongelman ratkaisumenetelmä on jaettavissa neljään eri vaiheeseen:
- Ymmärrä ongelma.
- Tee suunnitelma ongelman ratkaisemiseksi.
- Toteuta suunnitelma.
- Tarkastele ratkaisua.
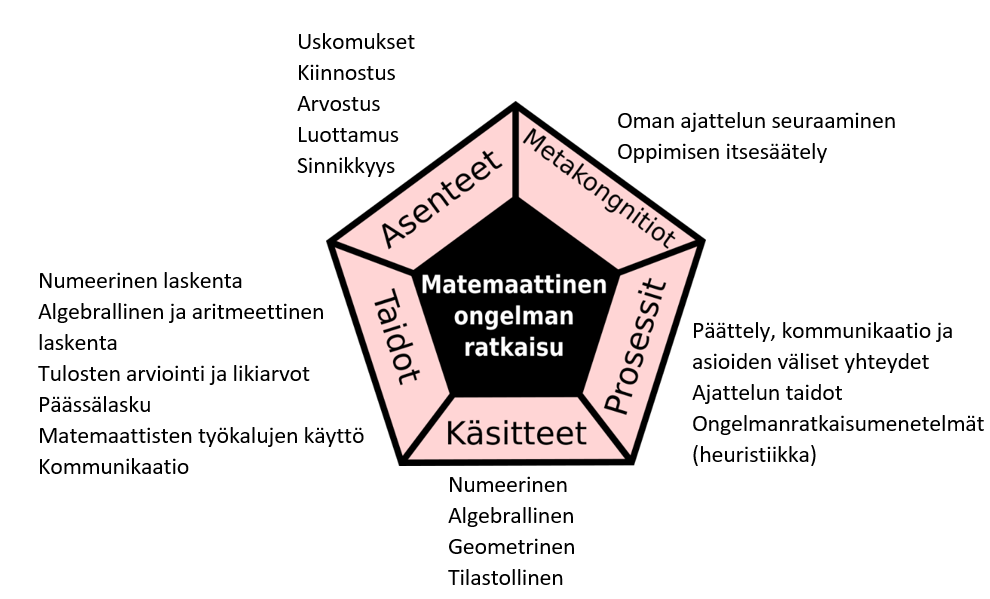
Singaporessa ongelmanratkaisu on jo vahvasti mukana alakoulussa keskeisenä osana kaikkia taito- ja käsitekeskusteluja. Ongelmat ovat usein monimutkaisia ja ei-rutiininomaisia, mutta toki rutiininomaisia ongelmiakin esiintyy. Pääpaino ongelmanratkaisussa on ongelmanratkaisustrategian löytäminen, joista tunnetuin on mallipiirroksen käyttö ongelmanratkaisussa. Aluksi mallipiirrosta käytetään rutiininomaisissa ongelmissa, mutta samaa ideaa sitten sovelletaan myös ei-rutiininomaisiin ongelmiin. Singapore-matematiikassa George Polyan ongelmaratkaisumenetelmässä korostuvat 1. ja 4. vaihe. Ensimmäisessä vaiheessa oppilaat yhdistävät ongelman aiempiin ongelmiin. Pohdintavaiheessa opiskelijat pohtivat, voidaanko menetelmää soveltaa muihin ongelmiin ja voidaanko ratkaisu löytää nopeammin. Myös oppilaiden asenteisiin kiinnitetään erityistä huomiota. Vuoden 1992 opetussuunnitelmassa ongelmaratkaisun viitekehys on esitetty viisikulmiona (Kuva 6).
Katsotaan vielä parin esimerkin avulla, kuinka piirrosta käytetään ongelmanratkaisumenetelmän apuna.
Esimerkki 3. Tyttöjä on koulussa 134 ja poikia 119. Kuinka monta tyttöä on enemmän kuin poikia?
 | Kun ongelmasta piirretään kuvio, niin on helposti havaittavissa, että kyseessä on yksikertainen vähennyslasku, jolloin vastaus saadaan vähentämällä tyttöjen määrästä poikien määrä. 154 – 119 = 35 Vastaus: Tyttöjä on 35 enemmän kuin poikia |
Esimerkki 4. Tyttöjä on koulussa 154 ja poikia 43 enemmän. Kuinka monta oppilasta on koulussa yhteensä?
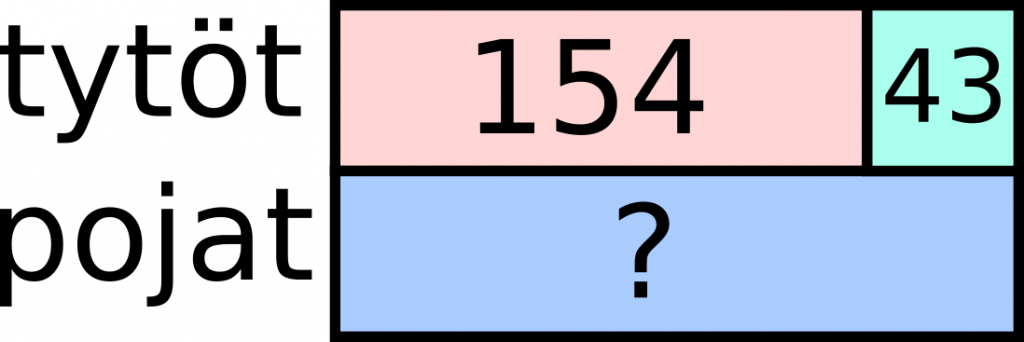 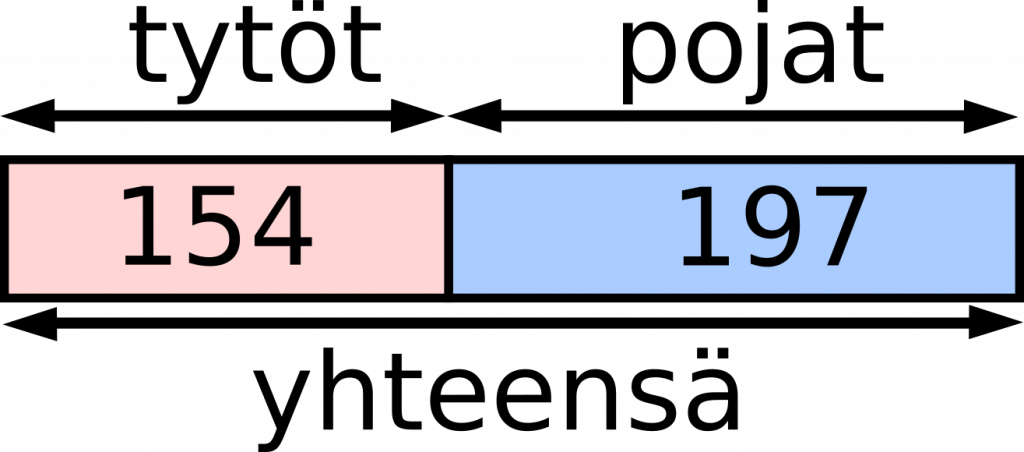 | Vaikka ongelma on jo monimutkaisempi, niin kuvion piirtämisen jälkeen havaitaan, että poikien määrä saadaan selville yhteenlaskulla: 154 + 43 = 197. Samoin oppilaiden määrä saadaan selville laskemalla yhteen tyttöjen ja poikien määrä eli 154 + 197 = 351. Tästä toisesta tilanteesta piirretään myös oma kuvansa. Vastaus: Oppilaita on yhteensä 351 |
Tärkeintä on huomata, että kuvat ongelmasta pidetään mahdollisimman yksinkertaisena. Myös Suomessa saattaa törmätä vastaavanlaisiin kuvioihin yhtälönratkaisun apuna. Se mikä Singapore-matematiikassa on kuitenkin erilaista verrattuna Suomeen, on, että piirroskuvioita käytetään paljon ja kaikissa laskutyypeissä. Sanallisten ongelmien ratkaiseminen piirtämällä kuviota apuna käyttäen aloitetaan jo 3. ja 4. luokalla ja sitä käytetään jatkuvasti aina yläkouluun 8. luokalle asti. Jos miettii, että näistä ongelmista tehtäisiin yhtälö, niin x:n lisääminen ongelmiin on vasta kolmas eli abstrakti vaihe. Tämä kolmas vaihe tuntuu jo helpolta, koska ongelma osataan jo ratkaista kuvion yhteen- ja vähennyslaskun avulla. Kyse on lähinnä merkitsemistavasta. Vertailu toisten maiden opetussuunnitelmiin on usein hedelmällistä ja ehkä Suomellakin olisi tästä jotain opittavaa, vaikka samankaltaisuuksiakin löytyy paljon.
Lue myös Dimension aikaisempi juttu samasta aiheesta
Singapore Mathin menestystarina, 13.3.2020 https://dimensiolehti.fi/singapore-mathin-menestystarina/
Lähteet
[1] Singapore math Wikipediassa https://en.wikipedia.org/wiki/Singapore_math
[2] Clark, Andy: Problem Solving in Singapore Math.
http://storage.cloversites.com/nextgenerationschool/documents/MIFProbSolving.pdf
[3] Maths — No Problem! -käyttäjän video Year 4 Singapore Maths Model Lesson: Measuring Area https://youtu.be/67Bd_UVsfTU
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista







