Viivojen taivuttelua
Sana ”viiva” herättää monenlaisia mielikuvia yhdysviivasta elämänviivaan ja janasta tikku-ukkoon. Viiva voi olla lyhyt tai pitkä, ohut tai paksu, suora tai koukeroinen, sininen tai punainen sen mukaan, kuka sen piirtää ja millaisella välineellä. Viiva on myös geometrinen muoto.
Avoimeksi sanotaan viivaa, jolla on päätepisteet, toisin sanoen joka alkaa jostakin ja päättyy johonkin muualle. Suljettu viiva ei ala eikä pääty mistään tietystä kohdasta, vaan sitä pitkin voidaan kulkea ympäri ja ympäri yhä uudestaan. Paperille piirrettynä se rajoittaa yhden tai useamman alueen. Viiva voi myös leikata itseään. Silloin avoimenkin viivan mutkat voivat rajata alueita.

Geometriassa viivalla ei ole leveyttä, vaan se on yksiulotteinen. Tämä tarkoittaa sitä, että viivaa pitkin voi kulkea vain eteen tai taakse. Ei voi poiketa oikealle tai vasemmalle eikä hypätä ylös tai alas. Monimuotoisuutta tuovat haarautumiskohdat ja risteykset. Tarkastelemme seuraavassa vain sellaisia viivoja, jotka ovat yhtenäisiä ja jotka eivät haaraudu eivätkä leikkaa itseään. Mitkä seuraavan kuvan viivoista ovat sellaisia? Vasemmanpuoleisia viivoja paraabelia, hyperbeliä, polynomifunktion kuvaajaa ja ruuviviivaa voidaan tarkastella äärellisinä viivoina, siis juuri sellaisina, joina ne on kuvaan piirretty, tai matemaattisina abstraktioina, joiden vapaiden päiden ajatellaan jatkuvan äärettömyyteen.
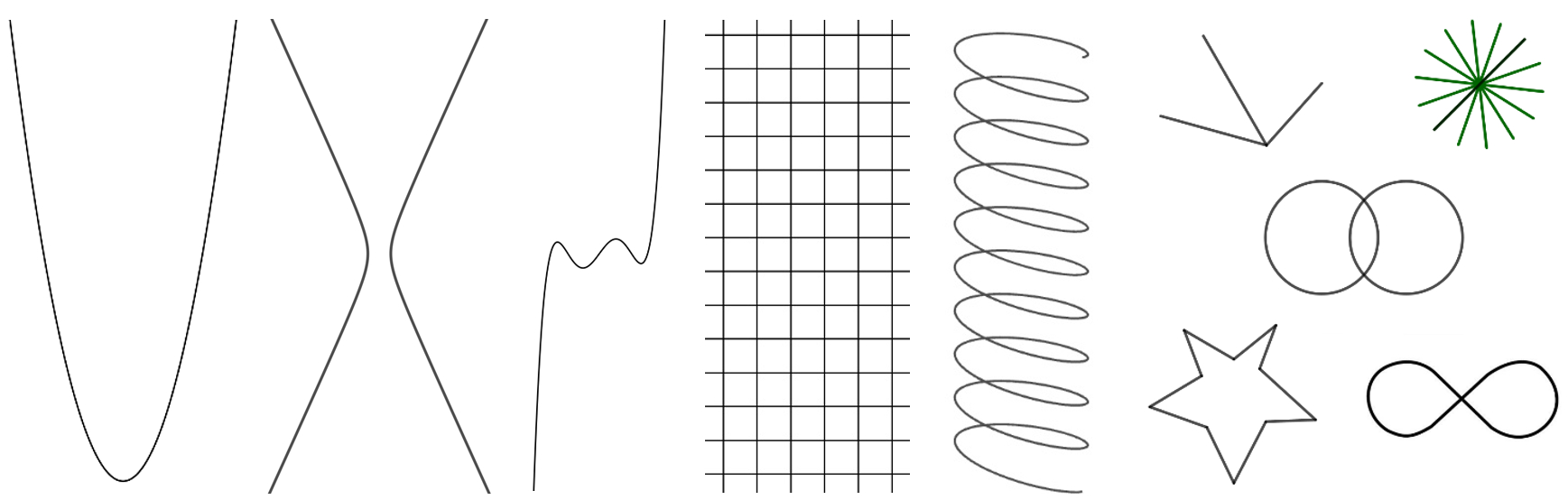
Vaikka viiva itsessään on yksiulotteinen muoto, niin suuri merkitys on sillä, millaisessa avaruudessa se asuu, matemaattisemmin sanoen millaiseen avaruuteen se on upotettu. Kuvaava esimerkki on edellisessä kuvassa binaaripuun oikealla puolella oleva ruuviviiva. Jos se on piirretty kaksiulotteiselle pinnalle, niin se leikkaa itsensä monessa kohdassa jokaisen lenkin jälkeen. Mutta kuva voidaan nähdä myös kolmiulotteisessa avaruudessa olevan ruuviviivan kaksiulotteisena projektiona. Kolmiulotteisessa avaruudessa ruuviviiva ei leikkaakaan itseään.
Tarkastelemme seuraavaksi tasolle piirrettyjä viivoja, jotka eivät haaraudu eivätkä leikkaa itseään. Kuinka monta eri lajia – viivojen luokkaa – tällaisia viivoja on? Ensikatsannolta saattaisi näyttää siltä, että viivat voitaisiin luokitella rajoitettuihin ja sellaisiin, joiden voidaan ajatella jatkuvan äärettömyyteen. Osoittautuu kuitenkin, että tämä ei ole olennainen ero. Samanlaisina – samaan muotoluokkaan kuuluvina – on nimittäin tarkoituksenmukaista pitää viivoja, jotka voidaan venyttää tai taivuttaa toisikseen. Matemaattisesti tämä tarkoittaa sitä, että on olemassa kuvaus, joka kuvaa viivan toiseksi viivaksi.
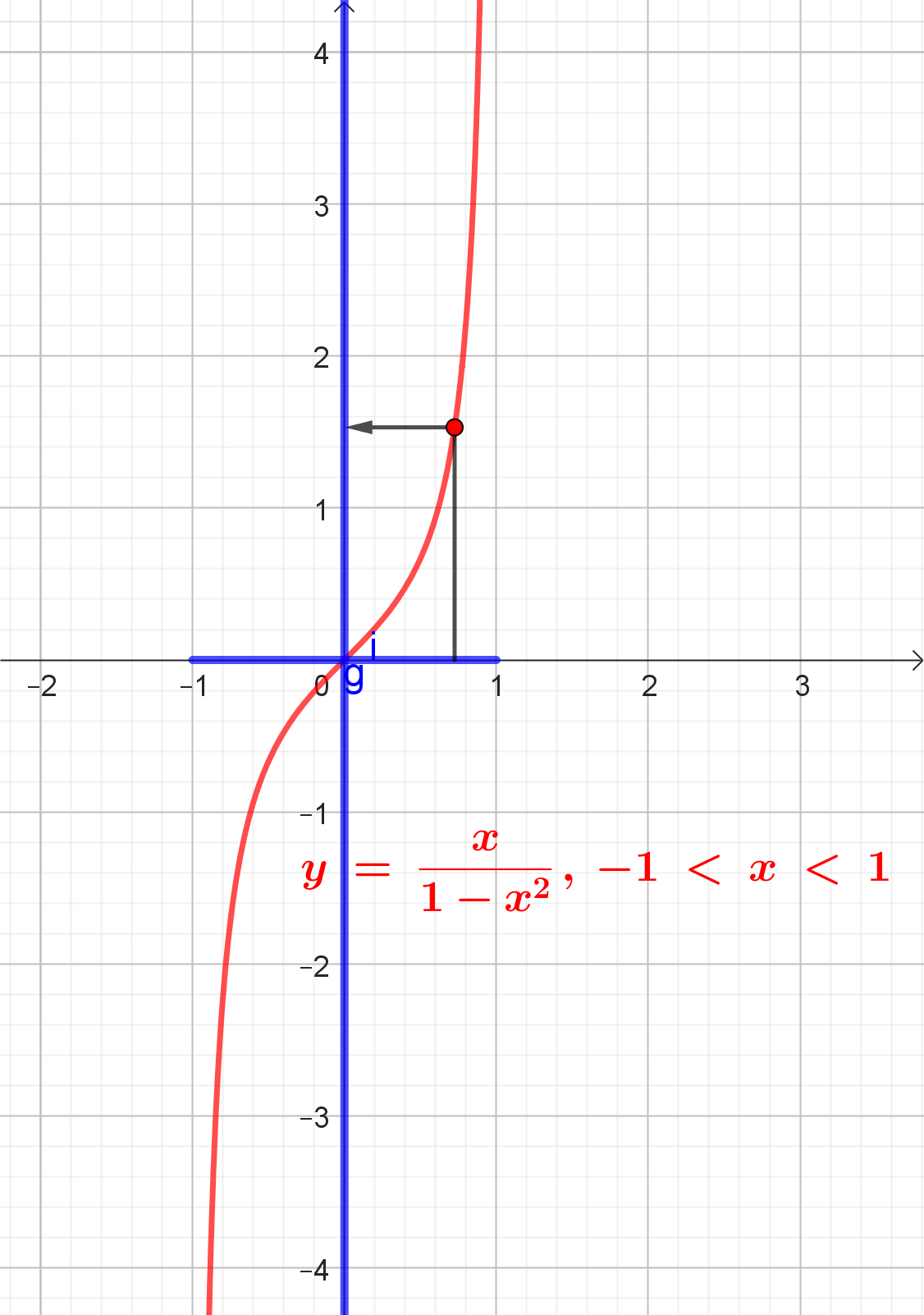
Olkoon esimerkkiparina jana ja suora: x-akselin väli ]–1, +1[ ja y-akseli. Funktio
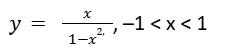
kuvaa janan suoralle kääntäen yksikäsitteisesti. Suora ja jana, jonka päätepisteet eivät ole mukana, ovat siis samaa muoto(luokka)a. Matematiikan kielessä tällaista samanlaisuutta merkitsevä sana on homeomorfisuus. Janan pituudella ei ole väliä, sillä eripituiset janat voidaan venyttää toisikseen. Samaan luokkaan kuuluvat mitkä tahansa muutkin itseään leikkaamattomat, haarautumattomat, avoimet viivat. Käyrät viivat voidaan oikaista suoriksi viivoiksi, siis janoiksi tai suoriksi. Äärellisen pituisia viivoja tarkastellaan ilman päätepisteitään. Silloin ne siis ovat samaa muotoluokkaa kuin suora. Siihen luokkaan kuuluvat myös äärettömyyteen ulottuvat viivat kuten paraabeli, hyperbelin toinen kaari, ruuviviiva sekä polynomifunktioiden niin kuin muidenkin funktioiden kuvaajat.

Suljetut käyrät tarvitsevat oman muotoluokkansa, sillä jos niitä ei katkaista, niin niitä ei voi venyttää tai taivuttaa janaksi. Tämän luokan yksinkertaisin muoto on ympyrä. On helppoa kuvitella, että mikä tahansa itseään leikkaamaton suljettu geometrinen muoto (kuvassa neliö) voidaan tasoittaa ympyrän muotoon, vaikka kuvauksen analyyttistä lauseketta ei olisikaan aina kovin helppoa keksiä. Voidaan siis sanoa, että kaksiulotteisessa avaruudessa on vain kahdenlaisia itseäänleikkaamattomia ja haaraantumattomia viivoja: suorankaltaisia avoimia viivoja ja ympyränkaltaisia suljettuja viivoja. Niiden tarkastelu monistoina johtaa havainnollisen geometrian ulkopuolelle abstraktiin topologiaan. Se menee jo paljon ulos tämän jutun perushahmotuksen tasoisesta tarkastelutavasta.
Kolmiulotteisessa avaruudessa on avointen viivojen lisäksi äärettömän monta suljettujen viivojen luokkaa. Tarkastellaan esimerkkinä solmuja. Kahdessa ulottuvuudessa solmuja ei oikeastaan ole, vaikka ympyrää nimitetäänkin joskus triviaalisolmuksi tai epäsolmuksi (engl. unknot). Kaikkia kolmiulotteisen avaruuden solmuja ei voida purkaa tai muotoilla toisikseen viivaa katkaisematta. Niitä luokitellaan risteysluvun mukaan. Risteyksellä tarkoitetaan kohtaa, jossa solmuviiva ylittää itsensä kaksiulotteisessa kuvassa. Ympyrän (triviaalisolmun) risteysluku on 0. Seuraava solmu on apilasolmu, tavallisessa puheessa umpisolmu (ylärivissä toinen vasemmalta). Sen risteysluku on 3. Kuvassa ovat seuraavina solmut, joiden risteysluku on 4, 5 tai 6. Alarivissä olevien solmujen risteysluku on 7. Erilaisten solmujen lukumäärä kasvaa nopeasti risteysluvun kasvaessa. Niinpä esimerkiksi erilaisia solmuja on jo 165, kun risteysluku on 10. Solmujen lukumäärän laskemiseen risteysluvun funktiona ei tunneta mitään kaavaa.
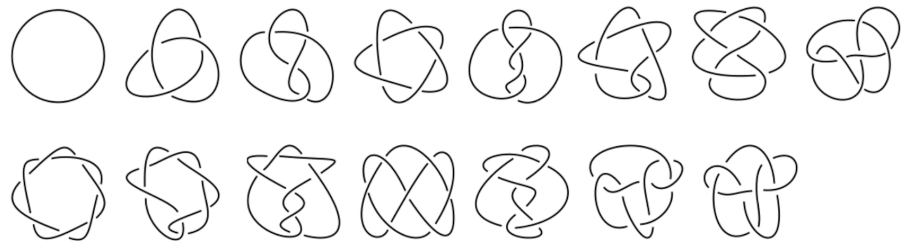
Huomaa, että risteysluvulla 1 ei muodostu solmua, vaan solmu purkautuu samaksi kuin triviaalisolmu eli ympyrä, samoin risteysluvulla 2. Neliulotteisessa avaruudessa ei ole muita solmuja kuin triviaalisolmu, sillä siellä kaikki solmut purkautuvat triviaalisolmuksi.








