Sangaku – Japanilaista temppeligeometriaa

Tiede ja teknologia

11.7.2024

Vuonna 1543 kolme portugalilaista haaksirikkoutui Kyushun saaren edustalla Japanissa ja tämän seurauksena portugalilaiset kauppiaat ja jesuiittalähetyssaarnaajat alkoivat saapua Japaniin. Pian portugalilaisten jälkeen saapuivat myös espanjalaiset fransiskaanit käännyttämään japanilaisia uuteen uskontoon. Tämä aiheutti epäluuloja Japanin hallitsijoissa.

Voittoisan taistelun jälkeen vuonna 1603 Tokugawa Ieyasusta tuli Japanin hallitsija eli shōgun. Ieyasu perusti päämajansa linnoituskaupunki Edoon (nykyinen Tokio), josta alkoi lähes 300 vuotta kestänyt Edo-kausi, jolloin Japani eristäytyi täysin ulkomaista ja ulkomaiset lähetyssaarnaajat karkotettiin Japanista 1600-luvun puoliväliin mennessä kokonaan ja kristinuskoon kääntyneet surmattiin. Koska lähes kaikki länsimaista tuleva oli kiellettyä Japanissa, myös modernin matematiikan uudet virtaukset 1700-luvulla jäivät saapumatta Japaniin. Eristyksen seurauksena matemaattinen pohdinta tapahtui hallituksen virkamiesten, joista moni toimi kirjanpitäjinä, kesken. Virkamiehillä oli usein paljon joutilasta aikaa, ja toisaalta ajattelun tuotokset haluttiin esille, jolloin matematiikka siirtyi Japanissa temppeleihin, jotka olivat kansan kohtaamispaikkoja. Matemaattiset ongelmat kirjoitettiin puisiin tauluihin, joita nimitettiin sangakuksi. Sangakussa oli kuvattuna kauniisti geometrisia ongelmia, ja ne olivat samalla taideteoksia ja uskonnollisten seremonioiden uhrilahjoja. Nämä geometriset ongelmat olivat nähtävillä kaikille temppelissä kävijöille, koska ne usein kiinnitettiin kattoon. Sangakun yhteydessä voidaan hyvinkin puhua kansanmatematiikasta, jota ratkoivat ja kehittivät niin japanilaiset matemaatikot, kuin naiset ja lapsetkin temppelissä käydessään. [1] [2]

Kun Japani eristäytyi ulkomaailmasta, niin samuraiden taistelutaidoille oli vähemmän käyttöä ja niinpä heistä tuli paremminkin hallituksen virkamiehiä kuin taistelijoita 1800-luvulle tultaessa. Valtion virkamiehen kuului osata myös matemaattisia taitoja ja osasta tulikin matemaatikkoja. Virkamiesten matemaattisia taitoja tarvittiin kirjanpidossa, veronkannossa ja pinta-alojen laskemisessa. Koska virkamiesten palkka oli huono, niin monet matemaatikot kunnostautuivat lisäksi opettajina yksityisissä kouluissa nimeltään juku. Matemaattisia tekstejä alettiin myös painamaan riisipaperille, mutta jos paperipainatukseen ei ollut varaa, niin matemaattinen ongelma voitiin siinä tapauksessa julkaista puutaulu sangakulle kirjoitettuna. Sangaku siis toimi sekä uskonnollisissa seremonioissa temppeleissä taiteellisena uhrilahjana että samalla antoi mahdollisuuden mainostaa omia matemaattisia tekstejä julkisesti. Shintolaisuus ja buddhalaisuus hyväksyvät monenlaiset uhrilahjat ja sangaku kävi sellaiseksi oikein hyvin, sillä olihan se samalla mielen hallinnan harjoittamista.

Monet sangakulle painetut ongelmat ovat helppoja ja muistuttavat paljolti antiikin Kreikan aikaisia geometrisia ongelmia, mutta osassa on hyvinkin pitkälle vieviä ideoita. Esimerkiksi matemaatikko Muramatsu Shigekiyo (1608–1695) laski 32 768-sivuisella monikulmiolla piin kaksikymmentäkaksi ensimmäistä numeroa. Tosin myöhemmin on todettu, että vain ensimmäiset kahdeksan numeroa oli laskettu oikein. Sitä vastoin ”Japanin Newton” Seki Takakazu (1640–1708) ratkaisi jo yhtälöryhmiä sekä toisen ja kolmannen asteen yhtälöitä. Seki myös kehitti diffrentiaali- ja integraalilaskentaa eli samaa kuin mitä Newton ja Leibniz tekivät samaan aikaan Euroopassa. Seki loi perustan japanilaiselle matematiikalle, jota kutsutaan nimellä wasan. Sekin työtä jatkoivat matemaatikot Matsunaga Yoshisuke (1692–1744) ja Ajima Naonobu (1732–1798), jotka kehittivät avaruuskappaleiden tilavuuden laskemista Sekin julkaisujen perusteella. Japanin eristyneisyyden kausi johti myös siihen, että japanilaisten matemaatikkojen saavutukset jäivät tuntemattomiksi muulle maailmaa. [1] [2]

valokuva vanhasta puutaulusta, jossa japaniksi tekstiä ja mallikuvia geometrian tehtävistä — Kuva 1: Sangaku, joka sijaitsee Emmanjin temppelissä Narassa. Kuva: Wikipedia Commons. [1]

Fujita Kagen (1765–1821) julkaisi ensimmäisen sangaku-ongelmien kokoelman Shimpeki sampo, jota seurasi jatko-osa Zoku shimpeki sampo. Ja hyvä että julkaisi, koska Edo-kauden jälkeen 1868 alkoi Japanin länsimaistaminen ja suurin osa puisista sangaku-tauluista hävitettiin silloin. Tähän päivään näistä puisista tauluista on säilynyt noin yhdeksänsataa. Nämä puiset taulut löysi uudestaan matematiikanopettaja Hidetoshi Fukagawa tutkiessaan kirjaston kirjoja, kun hän etsi mielenkiintoisia tapoja opettaa oppilaitaan. Hidetoshi perehtyi asiaan perusteellisesti ja julkaisi aiheesta kirjan Sacred Mathematics: Japanese Temple Geometry, joka kertoo sangaku-taulujen historian matemaattisten esimerkkien avulla. Kirja on ehdottomasti tutustumisen arvoinen. [1] [2]

Millainen matemaattinen ongelma sangaku-pulmatehtävä voisi esimerkiksi olla? Katsotaan kuvaa 2. Olkoon kuusikulmainen tasasivuinen monikulmio, jonka sisään voi piirtää kaksi tasasivuista kolmiota, jolloin muodostuu tähtikuvio. Piirretään tähtikuviossa olevalle sisemmälle kuusikulmiolle iso ympyrä, jonka keskipiste on O ja ympyrän säde on r. Piirretään lisäksi jokaiselle tähtikuvion sakaralle ympyrä niin, että se sivuaa isoa ympyrää ja ulkopuolella olevan kuusikulmion sivuja. Jos ison ympyrän säde on r = 10, niin mikä on tällöin pienen ympyrän säde t?

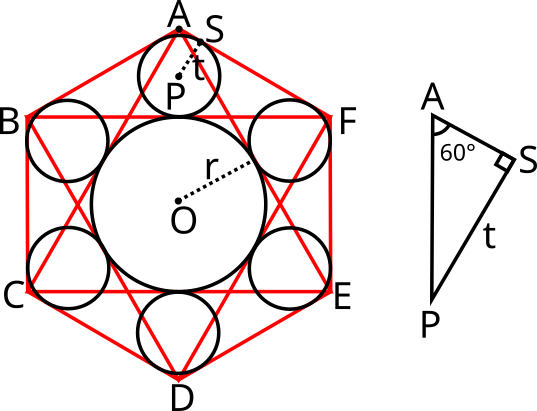
esimerkkikuva geometrian tehtävästä. — Kuva 2: Esimerkki sangaku-ongelmasta. Mikä on pienen ympyrän säde t, jos ison ympyrän säde r on annettu? Kuva: Tuomo Riekkinen.

Katsomalla pientä kolmiota APS saadaan sivujen suhde $\frac{t}{PA}=\frac{\sqrt3}{2}$, joka on sama kuin sin 60°. Matka

$OA=OP+PA=r+t+\frac{2}{\sqrt3}t$. Toisaalta $OA=2r$, jolloin saamme $t+\frac{2}{\sqrt3}t=r$ ja ratkaisemalla tästä t:n saamme $t=\frac{\sqrt3r}{\left(\sqrt3+2\right)}=\frac{\left(\sqrt3-2\right)\sqrt3r}{\left(\sqrt3-2\right)\left(\sqrt3+2\right)}=\left(2\sqrt3-3\right)r$

Jos r = 10, niin silloin t ≈ 4,641. [2]

Haluatko vielä itse kokeilla ratkaista geometrisen sangaku-pulmatehtävän? Alla olevassa kuvassa on suorakulmainen kolmio, jonka kateetit ovat 3 ja 4, sekä hypotenuusa on 5. Suorakulmaisen kolmion sisälle piirretään kaksi samankokoista ympyrää, jotka juuri ja juuri mahtuvat kolmion sisälle. Ympyrät sivuavat toisiaan ja kolmion tahkoja. Näillä annetuilla tiedoilla ratkaise ympyrän säteen suuruus. [3]

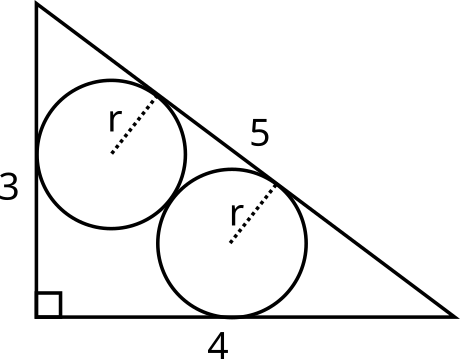
esimerkkikuva geometrian tehtävästä. Matemaattiset ongelmat kirjoitettiin puisiin tauluihin joita nimitettiin sangakuksi. — Kuva 3: Kuvan mukaisen suorakulmaisen kolmion sisälle piirretään kaksi ympyrää, jotka sivuavat toisiaan ja kolmion tahkoja. Selvitä ympyrän säde. Kuva: Tuomo Riekkinen [3].

Monet matematiikan harrastajat ovat palanneet näihin ongelmiin ja tehneet näistä malleja Geogebralla. Voit tutustua Geogebralla tehtyihin sangaku-pulmiin täällä: https://www.geogebra.org/search/sangaku