Kirjallisuutta: Matematiikan perusteita
Usko Lahti: Matematiikan perusteita havainnollisesti. MFKA 2025, 283 sivua.
Tekijä on eläkkeellä oleva Hyvinkään Sveitsin lukion matematiikanopettaja. Hän on tuottelias oppikirjailija. Finna tuntee kolmattakymmentä oppikirjaa, joissa hän on tekijänä. Tähän teokseen hän on koonnut sen, mitä tietää matematiikasta ja millaisena oppiaineena hän matematiikan näkee.
Kirja on todellinen järkäle. Ei ehkä niinkään sivumäärältään kuin asiasisällöltään. Tuntuu nimittäin siltä, että siinä käydään läpi koko se matematiikka differentiaalilaskentaa lukuun ottamatta, jota sain oppia Helsingin yliopistossa 1960-luvun loppupuolella, niin kuin varmaan kirjoittajakin, ikätoverini. Kirjan sisältö ja matematiikkakuva tuovatkin siksi mieleen vähintään yhtä paljon nostalgisia mielikuvia kuin matemaattisia ajatuksia.
Kirja jakaantuu 11 lukuun matemaattisesta päättelystä joukko-opin, reaalilukujen, euklidisen geometrian ja topologian kautta integraalilaskentaan. Harjoitustehtäviä on jokaisen luvun lopussa 5–38, eniten reaalilukuluvussa. Tehtäviin on myös ratkaisut niin kuin oppikirjoja kirjoittaneelta tekijältä on lupa odottaakin. Lisäksi mukana on yhdeksän sivua kommentteja (erikoisuutena erään kantakirjan isäoriiden säkäkorkeustaulukko), yksisivuinen matematiikan perussanasto (parikymmentä oppisanaa), symbolihakemisto, samoin yksisivuinen lähdeluettelo (30 julkaisua, runsaat puolet 1970-luvulta tai aikaisemmalta ajalta, mutta myös pari uutta verkkolähdettä) ja asiahakemisto (lähes 300 hakusanaa).
Kirjan johdanto alkaa tyyliin sopivasti antiikin kreikkalaisiakin vanhemmalta ajalta, lähes neljän tuhannen vuoden takaa kuvitteellisesta babylonialaisesta ”naismatemaatikosta” nimeltä Tiamat (sama nimi kuin meren ja kaaoksen alkujumalattarella), ajalta, jolloin matemaatikoita ei voinut olla olemassa, koska matematiikkaa ei ollut vielä keksitty. Jakson varsinaisena aiheena on yksi vanhimpia matemaattisia dokumentteja, neliön lävistäjää käsittelevä nuolenpääkirjoituksella kirjoitettu savitaulu.
Alkulauseessa tekijä sanoo, että ”olen pyrkinyt esittämään asiat havainnollisesti, mutta kuitenkin täsmällisesti”. Kirjan alkupuolella tuntuu siltä, että muodollisuus olisi ensisijaista ja havainnollisuus jäisi sen varjoon. Vaikutelma saattaa syntyä siitä, että alkupuolen aiheista monet ovat kovin tuttuja kokeneelle oppikirjailijalle ja että hän ehkä juuri siksi käsittelee niitä koulumatematiikan matemaattisina perusteina. Esitystapa on tutun matemaattinen: muodollisia määritelmiä, lauseita, apulauseita, todistuksia ja esimerkkejä. Toinen syy vaikutelmaani saattaa olla se, että olen tottunut ajattelemaan ainakin perusopetuksen matematiikkaa ymmärtämisen ja toiminnallisten menetelmien kautta, joten odotukseni havainnollisuuden suhteen ovat kohtuuttoman suuret.
Havainnollisuus alkaa näkyä vahvemmin, kun lähestytään kirjan puoliväliä ja päästään geometriaan. Luku alkaa muutaman sivun pituisella historiallisella katsauksella. Sitten tarkastellaan koulumatematiikan keskeisiä käsitteitä: kulmia, tason kuvauksia – myös analyyttisesti – ja pinta-aloja. Havainnollisuutta lisäävät monet GeoGebralla piirretyt kuvat. Luvussa on hauskoja yksityiskohtia, esimerkiksi hyperbeli peilattuna yksikköympyrän suhteen, ”geometrian Helenan” eli sykloidin parisivuinen käsittely, tikkataulun leikkaaminen ympyrän neliöinnin konkreettisena mallina ja Poincarén kiekon nelisivuinen tarkastelu esimerkkinä epäeuklidisista geometrioista. Geometria onkin kirjan luvuista pisin, lähes viidesosa kirjan sivumäärästä.
Seuraavissa kahdessa luvussa käsitellään euklidista avaruutta. Niissä mennään jo vähän ulos koulumatematiikasta, kun etäisyyden määrittelyn yhteydessä viitataan mielivaltaiseen metriseen avaruuteen ja käsitellään euklidisen avaruuden topologiaa. Topologiatarkastelujen rajaaminen kaksi- ja kolmiulotteiseen euklidiseen avaruuteen on viisas ratkaisu, sillä silloin voidaan käyttää perusgeometriasta tuttuja käsitteitä ja nojata sen luomiin konkreettisiin mielikuviin.
Raja-arvoa ja jatkuvuutta käsittelevän luvun havainnollisuus perustuu ehkä vahvimmin harjoituksiin ja esimerkkeihin. Osa niistä on kuitenkin kovin epätavanomaisia, esimerkiksi Rosenbrockin funktio, pistejonon

kuvaaja sekä babylonialaiseksi algoritmiksi nimitetyn lukujonon
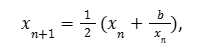
raja-arvo, missä x1 ja b ovat positiivisia lukuja ja n = 1, 2, 3, … Tämä on antiikin ajoista tunnettu Heronin menetelmä luvun b neliöjuuren arvon laskemiseen, mitä kirjassa ei sanota. Epätavanomaisuudestaan huolimatta näiden tapaiset esimerkit valottavat – ja ehkä ainakin jossain mielessä havainnollistavatkin – käsiteltävänä olevaa asiaa, jos lukija jaksaa niihin paneutua.
Kirjan viimeinen luku Lebesquen mitta menee käsittelytavaltaan ulos laskennallispainotteisesta koulumatematiikasta, vaikka se johdatteleekin integraalilaskentaan. Se on myös kirjan havainnollisin luku, ehkä siksi, että sitä eivät rasita koulumatematiikan esittämis- ja käsittelytapojen tottumukset. Ehkä kirjoittajakin on joutunut kehittelemään havainnollistavia mielikuvia oman ymmärtämisensä tueksi enemmän kuin loppuunkalutuissa koulumatematiikan aiheissa. Esimerkiksi valinta-aksiooman merkitys havainnollistuu joukkojen mitallisuuden tarkastelun yhteydessä.
Matematiikan perusteita kirjassa on ja havainnollisuuskin paranee luku luvulta. Sanalliset ilmaukset ovat välistä niin niukkoja, että lukija saa joskus pohtia tosissaan, mihin perustuu se, mitä tekijä sanoo. Kokonaiskuvaa matematiikasta tiedonalana kirjasta ei saa eikä se varmaan ole ollut kirjoittajan tarkoituskaan. Matematiikan historiaa valottavat siellä täällä olevat yksittäiset maininnat ja tätä kirjaa varten piirretyt matemaatikkojen muotokuvat. Matematiikan opettamista käsitellään vain yksisivuisessa ohjetekstissä Koulumatematiikkaa, oppimista ei ollenkaan.
Alkulauseen mukaan kirja on tarkoitettu opettamisen, opiskelun, soveltamisen ja harrastamisen avuksi. Ajatus on varmaan ihan oikea, mutta ainakin osa esimerkeistä ja tehtävistä sekä osin myös itse tekstikin on sen verran haastavaa, että kirjan käyttö itsenäisessä opiskelussa vaatinee erityistä harrastuneisuutta ja paneutumista. Se kyllä kannattaa, sillä pieniä, ilahduttavia yllätyksiä tulee varmasti vastaan enemmänkin matematiikkaa opiskelleelle tai harrastaneelle. Kaikkia niitä ei löydy asiahakemistosta, vaan ne tulevat eteen joskus vähän yllättävissäkin kohdissa kirjaa luettaessa. Sellainen on esimerkiksi ”pannukakkulause” (s. 135), joka koskee kahden erillisen, riittävän säännöllisen kuvion samanaikaista jakamista kahteen yhtenevään osaan yhdellä suoralla leikkauksella.







