Heilurin matematiikkaa ja koodausta – Fysiikan simulaation rakentaminen käytännössä
PhET-simulaatiot ovat tuttuja monelle, mutta voinko itse tehdä samanlaisen simulaation? Sehän onnistuu helposti, jos osaa jotain selaimessa pyörivää ohjelmointikieltä, esimerkiksi JavaScriptiä. JavaScriptiä helpompi lähestymistapa löytyy käyttämällä P5js-ohjelmointikieltä, joka on itse asiassa JavaScript-kirjasto. Tehdään simulaatio heiluriliikkeestä P5js-ohjelmointikielellä. Mutta käydään aluksi heilahdusliikkeen teoriaa.
Heilahdusliikkeen teoriaa
Vuonna 1656 hollantilainen fyysikko ja matemaatikko Christiaan Huygens rakensi heilurikelloja pohtien samalla heilurin toimintaa laskukaavojen avulla. Hän johti heilahdusajalle fysiikan oppikirjoista tutun laskukaavan [5]
$$T=2\pi\sqrt{\frac{r}{g}} \hspace{3cm}(1)$$
jossa todetaan heilahdusajan T kasvavan heilurin narun pituuden r kasvaessa. Huygensin pohdinnat heiluriliikkeestä jäivät keskeneräisiksi, joten italialaisranskalainen matemaatikko ja tähtitieteilijä Joseph-Louis Lagrange täydensi sitä vasta 100 vuotta myöhemmin johtamalla kuuluisan heiluriyhtälönsä (katso kaava 7). [6]
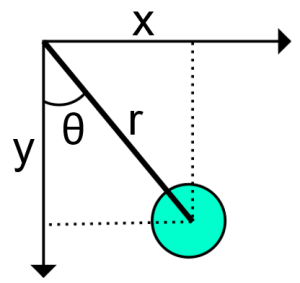
Heiluriliike on jaksollista edestakaista liikettä, joka tapahtuu ympyräradalla. Jos tiedetään ympyrän säde r eli heilurin langan pituus ja kulma θ, niin pallon paikka (x, y) koordinaatistossa voidaan helposti johtaa sinin ja kosinin avulla seuraavasti.
$$sin\ \theta =\frac{x}{r} \Leftrightarrow x=r\cdot sin\ \theta\hspace{3cm} (2)$$
$$cos\ \theta =\frac{y}{r} \Leftrightarrow y=r\cdot cos\ \theta \hspace{3cm} (3)$$
Kaavojen johtaminen voidaan havaita kuvasta 1.
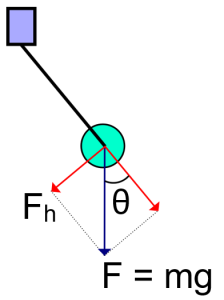
Heiluriliikkeen kulma θ ei ole vakio, eikä se kasva tai vähene lineaarisesti, koska siihen vaikuttaa painovoima ja voimahan tunnetusti aiheuttaa kiihtyvyyden. Mutta koska tässä on kyseessä ympyräliike, niin voidaan puhua tässä yhteydessä kulmanopeudesta ja kulmakiihtyvyydestä, jotka muuttavat kulman θ suuruutta. Kiihtyvyys ja voima liittyvät toisiinsa Newtonin II-lain mukaisesti eli F = ma. Kun katsomme kuvaa 2, niin sinin laskukaavalla voimme johtaa voiman Fh, joka aiheuttaa kulmakiihtyvyyden.
$$sin\ \theta =\frac{F_{h}}{F} \Leftrightarrow F_{h}=mg\cdot sin \ \theta\hspace{3cm} (4)$$
Voima Fh aiheuttaa momentin [7]
$$M={-F}_h\cdot\ r=-mg\cdot\ sin\ \theta\cdot\ r\ \hspace{3cm}(5)$$
Toisaalta pyörimisliikkeen momentti M on hitausmomentin I = mr2 ja kulmakiihtyvyyden a tulo [8]
$$M=I\cdot\ a=mr^2\cdot\ a\hspace{3cm} (6)$$
Yhdistämällä kaavat 5 ja 6 saadaan kuuluisa Joseph-Louis Lagrangen heiluriyhtälö.
$$mr^2\cdot\ a=-mg\cdot\ sin\ \theta\cdot\ r\ \Longleftrightarrow\ a=- \frac{g\cdot\ sin\ \theta}{r} \hspace{3cm} (7)$$
Eli kulmakiihtyvyys a riippuu painovoimasta g, kulmasta θ ja kääntäen heilurin pituudesta r. Tämän olet varmaan havainnut ihan käytännössä, mitä pidempi heiluri, sitä hitaammin heiluri heilahtaa, koska kulmakiihtyvyys on tällöin pienempi.
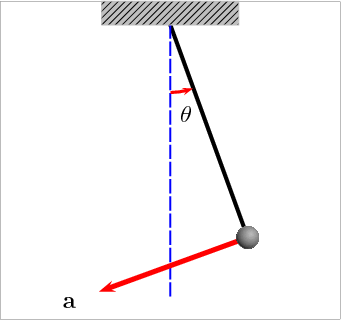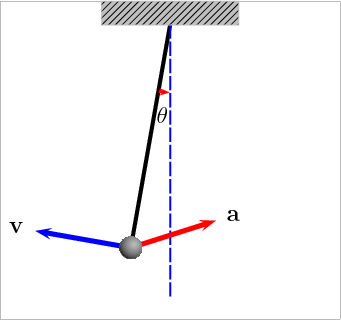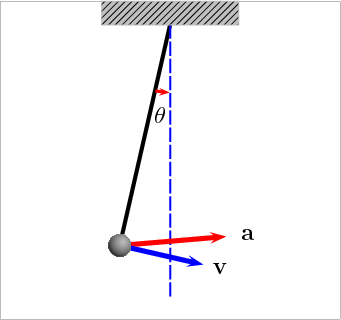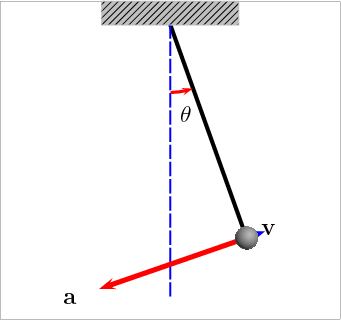
Kuva 3: Kulmakiihtyyden a ja kulmanopeuden v muuttuminen heilahduksen mukaan. Lähde: Wikipedia [3].
Kulmanopeus v lasketaan lisäämällä kulmakiihtyvyyden muutos at tähän eli
$$v=v_0+at\hspace{3cm} (8)$$
Ja uusi kulma θ saadaan tietysti lisäämällä tämä muuttunut kulma vt vanhaan kulmaan eli
$$\theta=\theta_0+vt \hspace{3cm} (9)$$
Ja tämän kulman θ avulla voidaan laskea heilurin uusi paikka xy-koordinaatistossa kaavojen 2 ja 3 avulla.
P5js -ohjelma
Rakennetaan edellisen idean pohjalta simulaatio. Perustetaan ohjelmaan seuraavat muuttujat: r = narun pituus, kulma = narun ja pystysuoran välinen kulma, g = putoamiskiihtyvyys, kulma_a = kulmakiihtyvyys ja kulma_v = kulmanopeus. Kuten kaavassa 7 todettiin, niin kulmakiihtyvyys voidaan kirjoittaa P5js-ohjelmointikielessä muotoon:
kulma_a = -g*sin(kulma)/r; (10)Oletuksena ohjelma käyttää radiaaniasteita, mutta laittamalla komento angleMode(DEGREES); setup-lohkoon, ohjelma saadaan käyttämään kulma-asteita. Kun ajatellaan, että ajan yksikkö on 1, niin kulmanopeuden kaava voidaan kirjoittaa muotoon:
kulma_v = kulma_v + kulma_a; (11)Siis kun kulmanopeuteen lisätään kulmakiihtyvyys, niin saadaan uusi kulmanopeus. Tämä on siis muuttunut kulma, joka lopuksi lisätään nykyiseen kulman arvoon eli
kulma = kulma + kulma_v; (12)Myös tässä ajatellaan, että ajan yksikkö on 1. Lopuksi tietysti lasketaan pallon xy-koordinaatit laskukaavoilla.
x = r*sin(kulma); (13)
y = r*cos(kulma);Nyt voimme rakentaa tästä kokonaisen ohjelman:
var r = 300; // Narun pituus
var kulma = 90; // Aloituskulma
var g = 10; // Putoamiskiihtyvyys
var kulma_a = 0; // kulmakiihtyvyys
var kulma_v = 0; // kulmanopeus
function setup () {
createCanvas(1000,600); // Ikkunan koko
strokeWeight(2); // Viivan paksuus
angleMode(DEGREES); // Kulma-asteet käytössä
}
function draw () {
background(220,220,200); // Taustaväri
translate(width/2,100); // Siirretään origon Paikka
fill(0,200,255); // Sininen täyttöväri
rect(-10,-100,20,100); // Piirrä suorakulmio
kulma_a = -g*sin(kulma)/r; // Lasketaan kulmakiihtyvyys
kulma_v = kulma_v + kulma_a;// Lasketaan kulmanopeus
kulma = kulma + kulma_v; // Lasketaan kulma
var x = r*sin(kulma); // Lasketaan x-koordinaatti
var y = r*cos(kulma); // Lasketaan y-koordinaatti
fill(0,255,0); // Vihreä täyttöväri
ellipse(x,y,50,50); // Piirretään ympyrä
line(0,0,x,y); // Piirretään viiva
}Ohjelman idea on se, että kulman θ suuruus vaikuttaa kulmakiihtyvyyteen a ja vastaavasti kulmakiihtyvyys a muuttaa kulmaa θ. Koska tämä laskutoimitus on draw -lohkon sisällä, niin laskut päivittyvät jatkuvasti eli kyseessä on jatkuva prosessi. Kulma θ muuttuu ja niin muuttuuvat ympyrän xy -koordinaatitkin.
Voit testata ohjelman toimivuuden täältä: https://editor.p5js.org/riekkinen/sketches/h7DSv3Bqj
Kokeile muuttaa narun pituutta: r, aloituskulmaa: kulma ja putoamiskiihtyvyyttä: g. Jos haluat realistisimman heilurin, jossa mukana on ilmanvastus eli kitka, niin muuta kaava 12 muotoon:
kulma = 0.999*kulma + kulma_v; (14)Kuten tämä esimerkki osoitti, simulaation rakentaminen ei ole kovinkaan vaikeaa. P5js-ohejlmointikieli antaa tähän hyvät selkeät komennot ja simulaation esittäminen ja jakaminen on helppoa, kun ensin luo P5js -ohjelmointiympäristöön omat tunnukset. Jos haluat vielä kehittää simulaatiota eteenpäin, niin P5js-kielessä lisäksi on valmiit liukupalkki -komennot, joilla vakioiden arvoja voidaan muuttaa helposti, niin kuin PhET -simulaatiossakin voi tehdä. Ohjelman alussa luodaan liukupalkille oma muuttujansa, esimerkiksi komennolla:
var painovoima; (15)Jonka jälkeen liukupalkki luodaan setup -lohkossa komennolla:
painovoima = createSlider(1,100,10); (16)
painovoima.position(10,10);Tässä liukupalkin arvot vaihtelevat välillä 1,…,100 ja oletusarvo on 10. Ja lopuksi liukupalkin lukema siirretään esimerkiksi muuttujan g-arvoksi draw -lohkossa komennolla:
g = painovoima.value(); (17)Tämä kokeilu jätetään lukijalle.
Simulaatiosta animaatioksi
Olisiko mahdollista luoda simulaatiosta animaatio? Kun ohjelman koodi ajetaan p5js-ympäristön sijasta Processing-ohjelmointiympäristössä ja viimeiseksi komennoksi lisätään saveFrame(); -komento, niin simulaation jokainen vaihe (frame) voidaan tallentaa bittikarttakuviksi. Nämä yksittäiset kuvat on helppo koostaa animaatioksi, esimerkiksi GIMP-kuvankäsittelyohjelmalla. Pieniä muutoksia koodiin joudumme tekemään, koska P5js pohjautuu JavaScriptiin ja Processing taas pohjautuu Javaan. Muutamme ohjelman kuvan 4 mukaiseen muotoon.
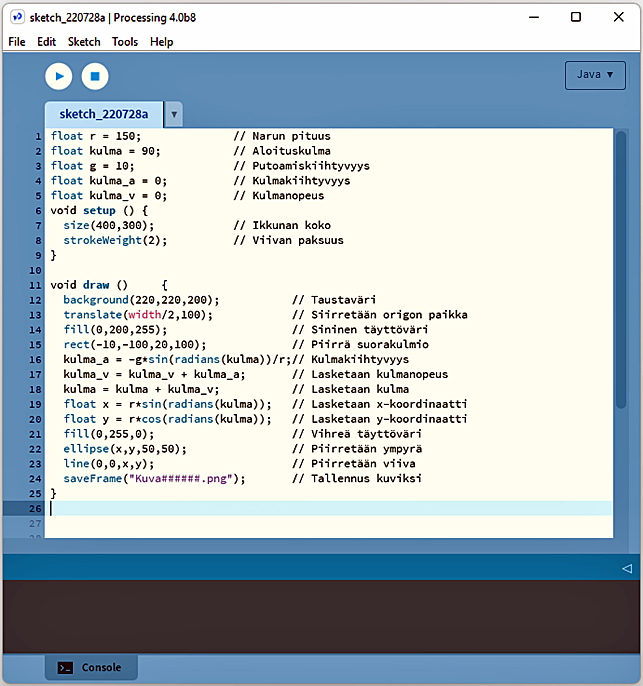
Sinun pitää ensin asentaa Prosecessing-ohjelmointiympäristö omalle tietokoneellesi, jotta voit kokeilla tämän koodin ajamista. Katso lähde [2] ja siellä kohta Download.
Ohjelmaa ei missään nimessä saa jättää pyörimään pitkäksi aikaa, koska saveFrame(); komento nopeasti täyttää kovalevyn kuvilla. Riittää kun käymme läpi yhden jakson eli edestakaisen heilahduksen. Tarvittaessa tallennukseen voit lisätä if -lauseen, joka lopettaa tallennuksen, kun jokin reunaehto täyttyy. Huomaat pieniä muutoksia koodissa. Muuttujan määrittely var on muuttunut float-määrittelyksi, function on muuttunut void-määrittelyksi ja createCanvas(); komento on muuttunut size(); -komennoksi. Lisäksi kulman laskemisessa käytämme radians() muunnoskomentoa. Muuten koodi on samanlainen. Tallennetuista kuvista on helppo koostaa animaation esimerkiksi GIMP-kuvankäsittelyohjelmalla. Toimi seuraavasti.
- Aukaise GIMP-ohjelma ja ota komento: Tiedosto | Avaa tasoina. Valitse ensimmäinen tiedosto, paina Shift-painike pohjaan ja valitse viimeinen tiedosto, jolloin saat kaikki kuvat valittua. Napsauta Avaa -painiketta.
- Kun kaikki kuvat ovat latautuneet kukin omille tasoillensa, niin ota komento: Tiedosto | Vie nimellä. Anna tiedostolle nimi esimerkiksi: heiluri.gif ja paina Vie -painiketta. Loppupääte gif on tässä pakollinen tieto.
- Laita kohtaan: As animation, ruksi. Määritä animaation nopeus, esimerkiksi 20 ms on tässä hyvä. Laita ruutujen poistotapa: ruutu per taso (korvaa). Myös muihin kohtiin voit laittaa ruksit, kuten: Ikuinen silmukka, Use delay entered above for all frames ja Use disposal entered above for all frames. Kuittaa lopuksi napsauttamalla Vie -painiketta.
- Kun menet Processing-ohjelman kansioon, jossa on kuvat ja ohjelman koodi, niin siellä on nyt myös heiluri.gif niminen tiedosto, jonka voit käynnistää kaksoisnapsauttamalla ja valitsemalla oletusohjelmaksi esimerkiksi jonkin selaimen, joka osaa näyttää animaation.
Lopputulos näyttää tältä:
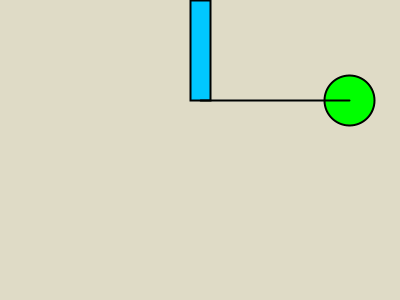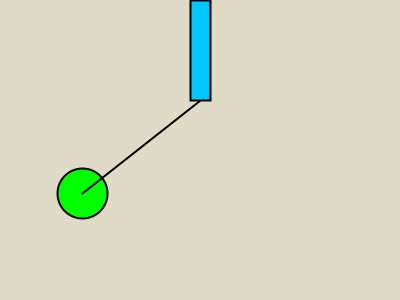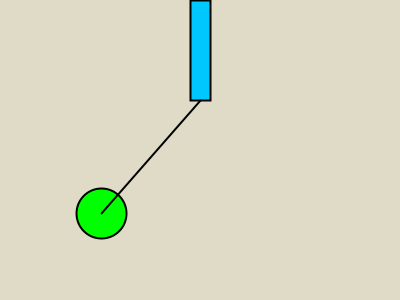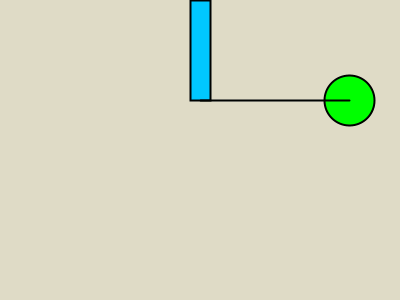
Kuva 5: Simulaatiosta luotu gif-animaatio
Lähteet
[1] P5js-ohjelmointiympäristö https://p5js.org/
[2]: Processing-ohjelmointikieli https://processing.org/
[3]: Wikipedia: Pendulum https://en.wikipedia.org/wiki/Pendulum
[4]: The Coding Train: Coding Challenge #159: Simple Pendulum Simulation https://youtu.be/NBWMtlbbOag
[5]: Wikipedia: Christiaan Huygens https://en.wikipedia.org/wiki/Christiaan_Huygens
[6]: Wikipedia: Joseph-Louis Lagrange https://en.wikipedia.org/wiki/Joseph-Louis_Lagrange
[7]: Wikipedia: Voiman momentti https://fi.wikipedia.org/wiki/Voiman_momentti
[8]: Wikipedia: Hitausmomentti https://fi.wikipedia.org/wiki/Hitausmomentti







