Hullun summa

Äkkiä ajatellen luulisi että tavallinen aritmeettinen summa (+) jos mikä on tarkka ja luotettava matemaattinen apuväline. Mutta onko se? Sehän riippuu täysin siitä millä tarkkuudella miellämme laskettavat objektit. Tätä kannattaakin tutkia tarkemmin.

Johdanto

Asetetaan koriin kolme omenaa ja kaksi banaania. Jos nyt kysymme montako hedelmää korissa on saamme lähes varmasti vastaukseksi viisi. Ja jos kysymme montako omenaa korissa on saamme mitä ilmeisimmin vastaukseksi kolme. Mutta jos valitsemme vaikkapa yhden noista omenoista ja haluamme tietää montako sellaista omenaa korissa on olemme hienoisissa vaikeuksissa. Kuinka ja millä tarkkuudella vastaus on selvitettävä ja ilmoitettava? Jonkun mielestä vastaus voi olla yksi, etenkin jos omena poikkeaa selvästi ulkonäkönsä puolesta kahdesta muusta omenasta. Toisen, hiukan suurpiirteisemmän henkilön mielestä sellaisia omenoita on korissa kolme kappaletta. Tämä kuulostaa enemmänkin arvailulta kuin matematiikan peruslaskutoimitukselta.

Zenonin paradoksi

Zenonin samanlaisuutta ja erilaisuutta koskevasta paradoksista Wikipedia toteaa näin: ”Samanlaisuutta ja erilaisuutta koskevan argumentin mukaan jos on olemassa monia asioita, niiden täytyy olla sekä samanlaisia että erilaisia keskenään, mikä on ristiriitaista. Argumentista ja sen perusteluista ei kuitenkaan tiedetä mitään muuta.” Näin on. Korin viisi hedelmää ovat sekä samanlaisia että erilaisia. Ne kolme omenaakin ovat keskenään samanlaisia ja erilaisia. En tietenkään tiedä varmasti mutta olettaisin että Zenon painiskeli juuri tämänkaltaisten ongelmien kanssa miettiessään samanlaisuutta ja erilaisuutta.

Hullun summa

Hullun summa on kehittämäni algoritmi, jota käytetään laskettaessa ”kuinka monta” jotain tiettyä objektia on jossain tietyssä joukossa.

Hullun summa ei aseta ylärajaa objektien (O₁, O₂, O₃, …) lukumäärälle. Objekteja voidaan lisätä laskettavaan joukkoon äärettömiin saakka. Jos jotkin objektit ovat riittävän samanlaisia voidaan niiden lukumäärä antaa algoritmissa kertoimena Q. Se toimii algoritmissa siis objektin painotuskertoimena.

Myöskään objektien piirteille (q_a, q_b, q_c, …) ei ole ylärajaa. Ulkoiset syyt tietysti asettavat rajat, koska on mahdotonta löytää, mitata, laskea tai muutoin selvittää objektin kaikki suureet. Objektin piirteitä voivat olla esimerkiksi massa, tilavuus, pinta-ala jne. Objektin piirteille (q) voidaan algoritmissa asettaa haluttaessa painotuskertoimia (w).

Hullun summa palauttaa halutun objektin näennäismäärän tietyssä objektien joukossa. Se on siis eräänlainen tavallisen aritmeettisen summan muunnos ja äärettömiin laajennettavissa ja tarkennettavissa. Sillä voi myös tutkia mahdollisen uuden objektin soveltuvuutta joukkoon. Lisäksi sillä voi selvittää joukossa jo olevan objektin kuuluvuutta joukkoon ja joukon kykyä tuottaa tiettyä objektia. Hullun summa summaoperaattorilla ilmaistuna:

Σ = summaoperaattori
i = muuttuja suureille q. Esim. massa (q_m), tilavuus (q_V), pinta-ala (q_A),… Suureen arvo sijoitetaan muuttujaan i
i´ = indeksimuuttuja suureille q. Esim. massa (q_m), tilavuus (q_V), pinta-ala (q_A),… Suoritusvuorossa olevan suureen ilmaisin. Suureen nimi/tunnus sijoitetaan indeksimuuttujaan i’
j’ = indeksimuuttuja objekteille O. Esim. omena (O_o), päärynä (O_p), banaani (O_b),… Suoritusvuorossa olevan objektin ilmaisin. Objektin nimi/tunnus sijoitetaan indeksimuuttujaan j’
kx = muuttuja valitun (laskettavan) objektin suureille. Esim. massa (q_m),
tilavuus (q_V), pinta-ala (q_A),… Suureen arvo sijoitetaan muuttujaan kx
kx´ = indeksimuuttuja valitun (laskettavan) objektin suureille. Esim. massa (q_m), tilavuus (q_V), pinta-ala (q_A),… Suoritusvuorossa olevan suureen ilmaisin. Suureen nimi/tunnus sijoitetaan indeksimuuttujaan kx´
Q = objektien lukumäärä (jos Q = 0 objektia ei ole)
w = suureiden painotuskerroin (jos w = 0 suuretta ei ole)
x = valitun objektin tunnus (O_a , O_b, O_c,, …)
n_x = valitun objektin näennäismäärä tietyssä joukossa.

Summakaava

Kaavana hullun summa näyttää tältä:

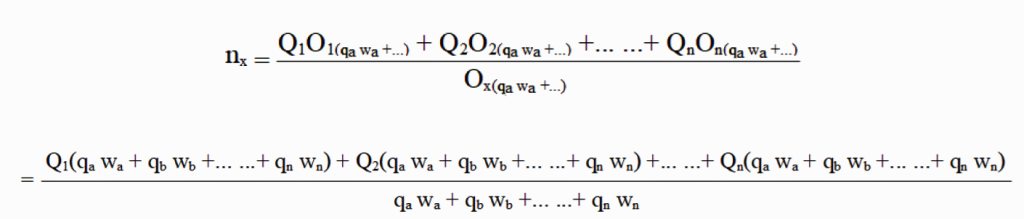
O₁ , O₂, … ,O_n= objektit
Q₁ , Q₂, … ,Q_n = objektin lukumäärä (objektin painotuskerroin).
q₁ , q₂, … ,q_n = suure
w_a , w_b, … ,w_n = suureen painotuskerroin
n_x = näennäismäärä [n kpl, näennäiskappaletta, ppcs, pseudo-pieces]

Esimerkki 1
Joukossa on kolme objektia joista tiedetään seuraavat arvot:
Objekti 1: m = 22 kg, V = 4 m³, A = 12 m²
Objekti 2: m = 15 kg, V = 3 m³, A = 8 m²
Objekti 3: m = 3 kg, V = 1 m³, A = 2 m²
Kaikkien objektien painotuskertoimet ovat nyt Q = 1 koska kaikkia on vain yksi kappale. Lisäksi mitään suuretta ei painoteta ja kaikkien suureiden painotuskertoimet ovat siis w = 1. Nyt halutaan tietää Objektin 1 näennäismäärä joukossa. Sijoitetaan seuraavaksi arvot yhtälöön:

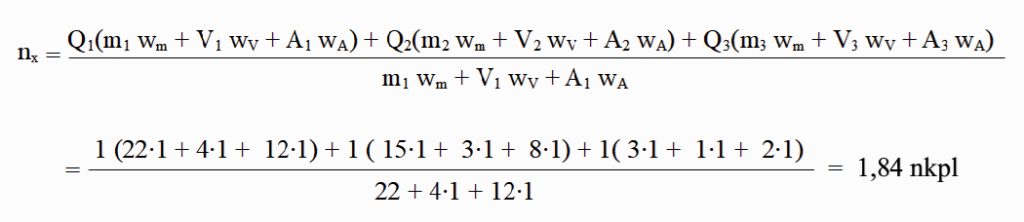
Joukko sisältää näiden suureiden mahdollistamalla tarkkuudella 1,84 nkpl objektia 1. Vastaavasti laskemalla saadaan että joukko sisältää 2,69 nkpl objektia 2 ja 11,67 nkpl objektia 3.

Esimerkki 2
Joukossa on nyt samat kolme objektia mutta lisäksi tulee yksi objekti 1:n kaltainen objekti:
Objekti 1: m = 22 kg, V = 4 m³, A = 12 m² (2 kpl)
Objekti 2: m = 15 kg, V = 3 m³, A = 8 m²
Objekti 3: m = 3 kg, V = 1 m³, A = 2 m²
Koska objekteja 1 on kaksi kappaletta annetaan sille painotuskerroin Q₁ = 2. Objektille 2 painotuskerroin Q₂= 1 ja objektille 3 painotuskerroin Q₃ = 1. Haluamme painottaa suuretta massa (m) muita tärkeämmäksi ja annamme sille tässä tapauksessa suureen painotuskertoimeksi w_m = 2. Muille suureille w_V = 1 ja w_A = 1. Nyt haluamme tietää objektin 1 näennäismäärän joukossa. Hullun summaa käyttämällä saadaan:

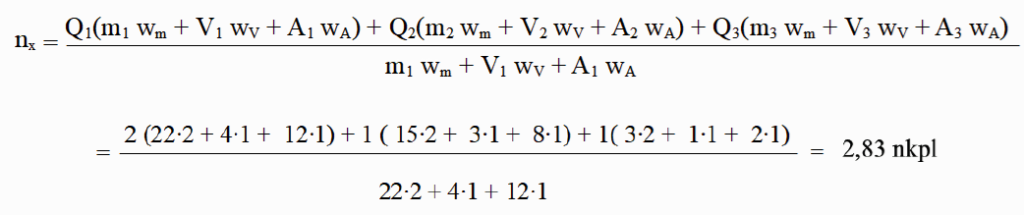
Joukko siis sisältää näiden suureiden mahdollistamalla tarkkuudella 2,83 nkpl objektia 1. Vastaavasti laskemalla saadaan että joukko sisältää 4,15 nkpl objektia 2 ja 18,89 nkpl objektia 3. Kyseessä on siis objektin näennäismäärä (pseudo amount) joukossa.

Lopuksi

Voidaan todeta, että mikään ei ole niin yksinkertaista kuin miltä ensi vilkaisulta näyttää. Edes tavallinen yhteenlasku ei ole itsestäänselvyys. Onko kaksi plus kaksi edelleen kuitenkin neljä? On se. Jollain tarkkuudella! Noh, ihan sama. Tai siis oikeastaan ihan eri. Ei kun…

---

Lisää luettavaa:

Zenonin pardoksit

Lue myös Heikin aikaisempi artikkeli: Ym­py­rän sä­teen las­ke­mi­nen seg­men­tin kaa­ren pi­tuu­den ja jän­teen pi­tuu­den pe­rus­teel­la. (31.7.2020)