Kesäkuun pulmat 2024: Monineliöt
Monineliöt (polyominoes) muodostuvat neliöistä, joista jokaisella on vähintään yksi sivu yhteisenä jonkin muun neliön kanssa. Seuraavista vasemmanpuoleinen on monineliö, mutta oikeanpuoleinen ei.
Tulostettava versio pulmista (pdf)
Yksinkertaisinta monineliötä, jossa on vain yksi neliö, voidaan sanoa triviaaliksi, sillä niistä voidaan koota mikä tahansa suorakulmio, jonka sivut ovat kokonaislukuja. Kahdesta neliöstä koostuvia monineliöitä – kaksneliöitä – on myös vain yksi, mutta se ei olekaan enää triviaali, koska on monta, jopa äärettömän monta suorakulmiota, jota ei voi niistä koota. Erilaisten monineliöiden lukumäärä kasvaa nopeasti, kun neliöiden määrä lisääntyy, Niinpä esimerkiksi kymmenestä neliöstä koostuvia erilaisia monineliöitä – kymmenneliöitä – on 4655 ja kahdestakymmenestä koostuvia 2 870 671 950, kun siirrolla, kierrolla tai peilauksella saatuja kuvioita pidetään samoina. Tällöin puhutaan joskus vapaista monineliöistä.
Tehtäviä:
1. Millaisia suorakulmiota ei voi rakentaa 2-neliöistä, siis kahdesta neliöstä muodostuvista monineliöistä?
2. Kuinka monta erilaista 3-neliötä on? Entä 4-neliötä? Siirtämällä, kiertämällä tai peilaamalla saatuja monineliöitä pidetään samoina.
3. Keksi muutamia suorakulmioita, jotka voidaan koota 3- tai 4-neliöistä. Entä onko sellaisia, joista ei voida rakentaa näistä?
4. Keksi pienin suorakulmio, jonka rakentamisessa on käytetty vähintään yksi jokaista 4-neliötä.
5. Kuinka monta erilaista 5-neliötä (viisneliötä) on? Keksi muutama suorakulmio, joka voidaan koota niistä. Ja jokin, jota ei voi koota.
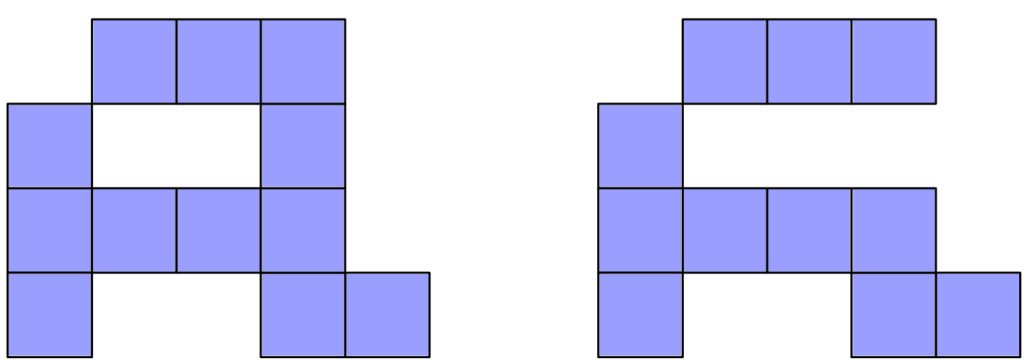
6. Keksi ainakin kolme 10-neliötä (kymmenneliötä), joista ainakin yhdessä on reikä.
Dimension pulmatehtävien ratkaisut MAOL ry:n sivuilla (vain jäsenille)







