Martin Gardner, metkan matematiikan mestari

Martin Gardner (1914–2010) on kaikkien aikojen tuotteliaimpia pulmatehtävien julkaisijoita. Hänen syntymästään tuli kuluneeksi sata vuotta muutama vuosi sitten.

Gardner [1] toimi lehtimiehenä ja myöhemmin vapaana kirjoittajana [2]. Tunnetuin hän on Scientific Americaniin vuosina 1957–1980 kirjoittamistaan lähes kolmesta sadasta kolumnista [3] ja yli sadasta kirjasta [4]. Kolumneissaan hän teki tunnetuksi monien matemaatikkojen töitä, esimerkiksi Conwayn elämänpelin, Penrosen laatat ja Mandelbrotin fraktaalin. [5] Hänen matemaattisia pulmia sisältävistä kirjoistaan on suomennettu vain kolme: Älyniekka (1965), Ongelmatarinoita (2003) ja Matemaattisia huvituksia (2011). 

Gardnerin tehtävät eivät aina vaadi koulumatematiikan tapaista laskemista, vaan pikemminkin paneutumista ja oivaltamista. Valaiseva esimerkki on tehtävä, jossa kysytään kuution samasta kärjestä lähtevien sivutahkojen lävistäjien välistä kulmaa (kuva). 

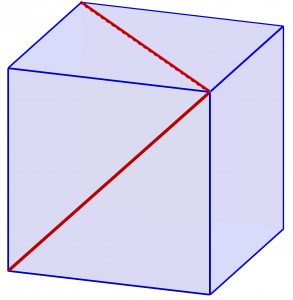
Tyypillisiä Gardnerille ovat myös kuvion jakamistehtävät. Kahdeksantoistakulmio on jaettava kahdeksi yhteneväksi osaksi yhdellä, ei välttämättä suoralla leikkauksella. [6]

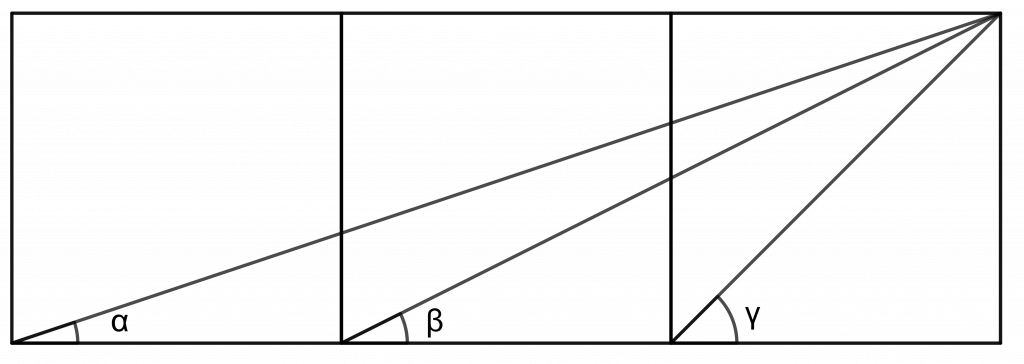
Vähän enemmän alkeisgeometriaa tarvitaan sen osoittamiseen, että kolmeen vierekkäiseen neliöön piirretyt kulmat α, β ja γ (kuva) täyttävät ehdon

α + β = γ 

mutta siinäkin tarvitaan vain pieni apupiirros ja yhdenmuotoisia kolmioita [7].

Erityisen suosituiksi nousseita kolumnien aiheita [8] ovat olleet metkan matematiikan (engl. recreational mathematics) alaan kuuluvat monineliöt [9] (engl. polyominoes), joustomonikulmiot [10, 11], (engl. flexagons), esimerkiksi joustonelikulmio (kuva [12] ja video [13]), C. M. Escherin geometrisaiheinen taide [14], laatoitukset [15] ja julkisen avaimen salakirjoitusjärjestelmät. Aiheet eivät rajoittuneet vain matematiikkaan, vaan Gardner käsitteli kirjoituksissaan myös fysiikkaa [16], taikatemppuja ja monia muitakin asioita.

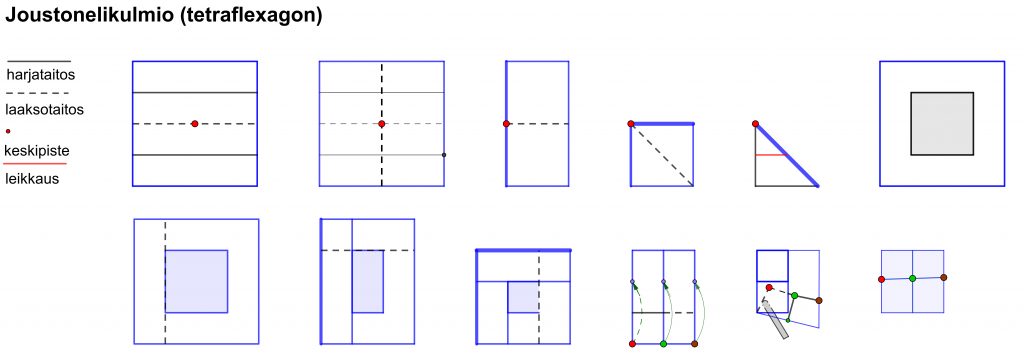
Matemaattisten pulmien harrastaja voi nähdä Gardnerin tehtävät ratkaisujen pohtimisen lisäksi myös ajattelun välineiden antajina ja pohjana uusien tehtävien kehittelylle. Niinpä esimerkiksi edellä oleva, kahtia jaettava kahdeksantoistakulmio on kaksitoistaneliö samoin kuin joustonelikulmion teko-ohjeen kuudes vaihe (ylärivin oikeanpuolimmainen). Jälkimmäisessä on vain reikä keskellä. Ajattelutapa synnyttää uusia kysymyksiä ja tehtäviä. Onko tämä ainoa reiällinen kaksitoistaneliö? Mikä on pinta-alaltaan pienin monineliö, jossa on reikä? Kuinka monta erilaista reiällistä monineliötä on kullakin osaneliöiden lukumäärän arvolla? Kuinka monta yhdellä leikkauksella kahteen yhtenevään osaan jaettavaa monineliötä on kullakin osaneliöiden lukumäärän arvolla? Entä, jos leikkausviiva voi kulkea vain osaneliöiden sivuja pitkin? Joustonelikulmion taitteluohje (kuva yllä) on itsessään konkreettinen askartelutehtävä, jota ei Gardnerin kirjoituksissa ole.

Viitteet

[1] Martin Gardner (1914-2010) osoitteessa http://martin-gardner.org/

[2] Wikipedia-artikkeli Martin Gardner osoitteessa https://en.wikipedia.org/wiki/Martin_Gardner

[3] Wikipedia-artikkeli List of Martin Gardner’s Mathematical Games columns osoitteessa https://en.wikipedia.org/wiki/List_of_Martin_Gardner_Mathematical_Games_columns

[4] Luettelo Gardnerin kirjoista Books by Martin Gardner osoitteessa https://www.thriftbooks.com/a/martin-gardner/203163/

[5] Mulcahy, Colm (2014): Martin Gardner, puzzle master extraordinaire osoitteessa https://www.bbc.com/news/magazine-29688355

[6] Bellos, Alex (2014): Can you solve Martin Gardner’s best mathematical puzzles? osoitteessa https://www.theguardian.com/science/alexs-adventures-in-numberland/2014/oct/21/martin-gardner-mathematical-puzzles-birthday

[7] Bellos, Alex (2014): Solutions to Martin Gardner’s best mathematical puzzles osoitteessa https://www.theguardian.com/science/alexs-adventures-in-numberland/2014/oct/27/solutions-to-martin-gardners-best-mathematical-puzzles

[8] Mulcahy, Colm (2014) The Top 10 Martin Gardner Scientific American Articles osoitteessa https://blogs.scientificamerican.com/guest-blog/the-top-10-martin-gardner-scientific-american-articles/#

[9] Korhonen, Hannu (2020): Askartelua ja aivojumppaa: mekaaniset pulmat 2 osoitteessa https://dimensiolehti.fi/askartelua-ja-aivojumppaa-mekaaniset-pulmat-2/

[10] Geometric Toys to Make: Flexagons osoitteessa https://www.auntannie.com/Geometric/Flexagon/

[11] Martin Gardner and Flexagons osoitteessa https://www.youtube.com/watch?v=zo2XG9_pXvQ

[12] Geogebra-materiaali Origamitaitto-ohje joustonelikulmiolle osoitteessa https://www.geogebra.org/m/scd2d5wr

[13] Joustonelikulmion taitteluohje osoitteessa https://www.youtube.com/watch?v=Dp_zb-Emstg. Austin Parks & Recreation, Northwest Recreation Center.

[14] Korhonen, Hannu (1982): Taiteen ja matematiikan yhteyksiä 4. Järjestys ja järjettömyys Escherin teoksissa. Funktio 2/1982 s. 2–5.

[15] Korhonen, Hannu (2019): Laatoitusten geometriaa. Dimensio 13.5.2019 osoitteessa https://dimensiolehti.fi/laatoitusten-geometriaa/

[16] Martin Gardner and Physics osoitteessa http://martin-gardner.org/Physics.html