Mikko Rahikan GeoGebra-sarja – Osa 3: Jono -komento GeoGebrassa

Opetus

20.3.2019

GeoGebran Jono-komento (Sequence) vastaa perinteisissä ohjelmointikielissä for-next -silmukkaa. Sen avulla saadaan luotua tarvittaessa pitkiäkin listoja, joiden jäseninä voi olla muita GeoGebran objekteja; lukuja, pisteitä, yhtälöitä, taso- ja 3D geometrian objekteja jne.

Jonoa voi käyttää monella eri syntaksilla, sillä voi olla 1 – 5 syötettä. Tutustutaan näihin esimerkkien avulla. Kirjoitan seuraavassa komennot GeoGebra Classic 5:n CAS:iin tai Syöttökenttään. GeoGebra 6:n CAS:issa komennot toimivat täsmälleen samalla tavoin.

Kun syötteenä on yksi luku n, niin Jono tuottaa listan, jonka alkioina ovat luvut 1, …, n.

Jono(5) → {1, 2, 3, 4, 5}

Kun syötteenä on kaksi lukua m ja n, niin Jono tulostaa listan, jonka alkioina ovat luvut m, …, n.

Jono(3,8) → {3, 4, 5, 6, 7, 8}

Jono(8,3) → {8, 7, 6, 5, 4, 3}

Kun syötteenä on kolme lukua m, n ja k, niin Jono tulostaa listan, jonka alkioina ovat luvut m:stä n:ään siten, että m:stä alkaen otetaan joka k:s luku n:ään asti. Listan alkiot muodostavat aritmeettisen jonon.

Jono(2,13,3) → {2, 5, 8, 11}

Jono(1/2, 42/13, 1/3) → {0.5, 0.833, 1.167, 1.5, 1.833, 2.167, 2.5, 2.833, 3.167}

Kun Jonon syötteessä on viisi oliota, niistä ensimmäinen on muuttujan sisältävä lauseke, toinen on muuttuja, kolmas muuttujan ensimmäinen arvo, neljäs muuttujan viimeinen arvo ja viides askelväli. Viimeisen voi jättää pois, jolloin askeleen pituus on yksi. Jos käyttää muuttujaa Jonon lausekkeessa, niin GeoGebra pyrkii tuottamaan tulostelistaansa tarkat arvot.

Jono(k^2, k, -3, 3) → {9, 4, 1, 0, 1, 4, 9}

L1≔Jono(k,k,1/2,42/13,1/3) → L1≔{1/2, 5/6, 7/6, 3/2, 11/6, 13/6, 5/2, 17/6, 19/6}

Summa-komento laskee syötelistan alkioiden summan.

Summa(L1) → 33/2

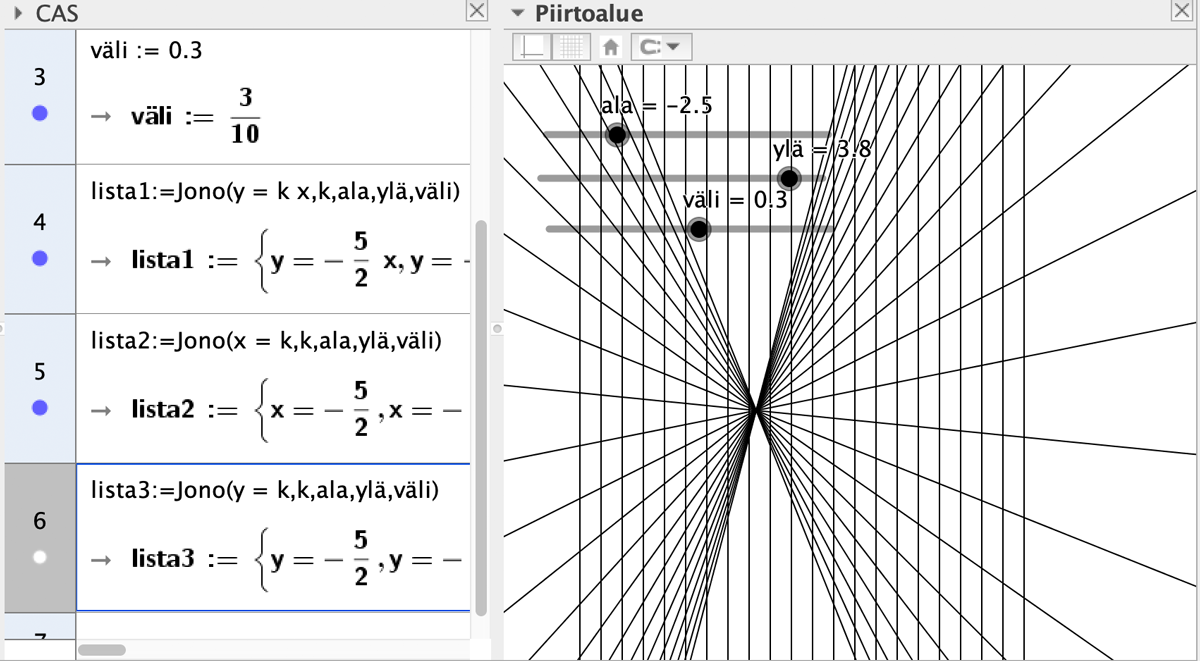
Katsotaan muutamia esimerkkejä, mitä Jonolla saa aikaiseksi. Luodaan ensin liu’ut ala, ylä ja väli. Niiden avulla voidaan säätää Jonon muuttujia. Luodaan ensin kaksi suoraparvea: y = k x ja x = k. Kirjoitetaan Syöttökenttään

ala = 5 ylä = 5 väli = 5

Kun klikataan Algebraikkunassa vasemmalla oleviin ympyröihin, niin liu’ut ilmestyvät näkyviin piirtoalueelle. Luodaan origon kautta kulkevista suorista lista1 ja y-akselin suuntaisista suorista lista2.

lista1:=Jono(y = k x,k,ala,ylä,väli) → lista1:= {y = (-5 / 2 * x), y = (-11/ 5 * x), …, y = 19/5}

ja y-akselin suuntaiset suorat

lista2:=Jono(x = k,k,ala,ylä,väli) → lista2:= {x = -5 / 2, x = -11 / 5, … , x = 19 / 5}

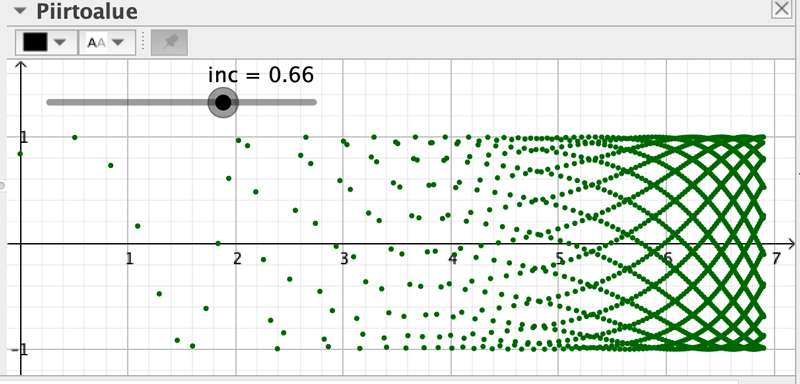
Edellisessä esimerkissä tuotettiin suoria, luodaan seuraavaksi (x, y) pisteitä koordinaatistoon. Michael Borcherds’n ja Dag Oscar Madsenin LinkedIn keskustelusta löytyi seuraava mielenkiitoisia kuvioita tuottava yhden rivin pisteistö. Tässä inc-liukusäädin saa Ominaisuudet ikkunassa arvoja: Min: 0.01, Max:1, ja Askelväli: 0.01. Kun muuttujan inc-arvoa muuttaa, pisteet näyttävät joillain arvoilla tuottavan kauniita käyriä. Miksiköhän?

Jono((ln(n), sin(n)), n, 1, 1000, inc)

Joskus kaukaisessa menneisyydessä 1980-luvun lopussa tutustuin Logo-ohjelmointiin. Logon kilpikonnagrafiikan avulla sai yksinkertaisilla ohjelmanpätkillä mielenkiintoisia kuvia tasolle. Logon innoittaman innostuin tutkimaan tähtikuvioita ihan omaksi ilokseni.

Tehdään sovellus, jonka avulla voi tutkia tähtikuvioita, joiden kärjet ovat yksikköympyrään piirretyn säännöllisen monikulmion kärkipisteissä. Luodaan aluksi liukusäätimet n ja m. Liukujen asetuksissa n saa arvot Min:3, Max:50, Animaatioaskel:1 ja m arvot Min:1, Max: n-1 ja Animaatioaskel: 1. Luodaan seuraavaksi yksikköympyrään lista karjet säännöllisen monikulmion kärkipisteistä. Puolipiste koordinaatiston pisteen erottimena tuottaa pisteet napakoordinaateissa.

karjet = Jono((1; aa 2π / n), aa, 1, n)

Monikulmio(A, B, n) -komento tuottaa säännöllisen n-kulmion, siten, että yksi sivu on jana AB. Komento karjet(x) tuottaa karjet listan x:n jäsenen.

kuvio1 = Monikulmio(karjet(1), karjet(2), n)

Tähtikuvion kärkiä varten tarvitaan jakojäännöksiä. Otetaan karjet listasta joka m:s jäsen, toistetaan tätä n kertaa. Annetaan listalle nimi tkarjet. Koska listan jäsenet numeroidaan 1, …, n pitää jakojäännökseen lisätä 1, jotta järjestysnumeroksi ei tulisi nolla.

tkarjet = Jono(karjet(Jakojäännös(i, n) + 1), i, 1, n m, m)

Kun Monikulmio-komennossa on syötteenä lista, niin se tuottaa monikulmion siten, että listan pisteet ovat kärkipisteinä. Tähtikuvio syntyy komennolla Monikulmio(tkarjet).

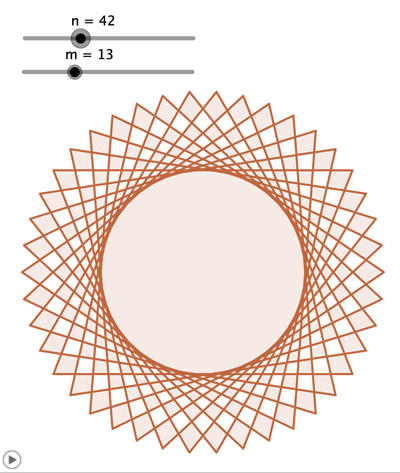
Joillain muuttujien arvoilla m ja n syntyy tähtikuvioita. Esimerkiksi m = 5 ja n = 2 tuottaa pentagrammin. Usein matemaattisessa kirjallisuudessa käytetään säännölliselle viisikulmiolle merkintää {5/1} ja pentagrammille merkintää {5/2}. Aina ei synny tähtikuviota, {6/2} on kolmio ja {6/3} on jana. Joskus syntyy tähtikuvio, mutta siinä ei välttämättä ole n kappaletta kärkipisteitä, {18/4} on tähtikuvio, jossa on 9 kärkeä.

Tästähän saa mielenkiintoisen tutkimustehtävän oppilaille. Milloin tulee tähtiä, milloin säännöllisiä monikulmioita ja milloin janoja? Itse asiassa ennen tätä oppilaat voisivat luokitella minkä tyyppisiä kuvioita eri n:n ja m:n arvot tuottavat. Millä n:n arvoilla ei synny lainkaan tähtiä? Millaiset n:n arvot tuottavat tähtiä kaikilla m:n arvoilla 1 < m < n – 1? Lahjakkaammat oppilaat ja opettajat voivat myös pohtia löytämiensä lauseiden todistuksia.

Monte Carlon sammakko

Monte Carlo -menetelmässä käytetään satunnaislukuja, kun simuloidaan hankalan ongelman ratkaisua. Anders Skjäl esitti MAOL eKerhon Facebook-ryhmässä syyslomahupitehtävän: ”Sammakko hyppää yhden pituusyksikön satunnaiseen suuntaan ja sen jälkeen puoli pituusyksikköä uudessa satunnaisessa suunnassa. … Määritä sammakon lopullisen sijainnin todennäköisyysjakauma.” Hetken aikaa ongelmaa pohdittuani totesin, että tuo vaikuttaa ilkeältä integroimisongelmalta, niinpä päätin simuloida sammakon hyppelyä.

Luodaan hyppelyjä kuvaava muuttuja n. Sen yläraja kannattaa pitää mielekkäässä kokoluokassa. Järkevä maksimikokoluokka on noin 10 000–100 000 riippuen koneen tehosta ja GeoGebra-versiosta. Miljoona jumittanee koneen.

n = 100

Ensin sammakko hyppää satunnaiseen pisteeseen, jonka napakoordinaatit ovat (1, α), missä kulma α valitaan satunnaisesti väliltä 0 ≤ α < 2π. Sen jälkeen se hyppää samalla logiikalla (½, β). GeoGebra osaa laskea tämän tyyppisen vektoreiden yhteenlaskun xy-koordinaatiston pisteiden välisenä yhteenlaskuna. GeoGebran random()-funktio tuottaa satunnaisluvun. Niinpä sammakon hypyt saadaan simuloitua komennolla

sami = Jono((1; 2π random()) + (0.5; 2π random()), k, 1, n) sami = {(1.42; 244.17°), (0.51; 119.69°), …, (1.46; 33.35°)}

Koordinaatistoon ilmestyy pisteitä 1/2 ja 3/2 -säteisten ympyröiden väliin. Koska sami-listan pisteet on esitetty napakoordinaateissa, niiden etäisyydet ovat sami-listan pisteiden ensimmäiset koordinaatit. Ne saa irrotettua napakoordinaateissa esitetystä pisteestä abs-funktiolla, joka kertoo pisteen etäisyyden origosta. Vastaavasti suuntakulman saa arg-funktiolla.

etlista = Jono(abs(sami(k)), k, 1, n) etlista = {1.42, 0.51, …, 1.46}

Luodaan frekvenssien laskennassa tarvittavat välit listaan nimeltä luokat. Alaraja on 0,45, yläraja on 1,55 ja välin pituus 0,1.

luokat = Jono(0.45, 1.55, 0.1) luokat = {0.45, 0.55, 0.65, 0.75, 0.85, 0.95, 1.05, 1.15, 1.25, 1.35, 1.45, 1.55}

Lasketaan etäisyyksien frekvenssit edellä luodun luokat-listan väleissä Frekvenssi(<Luokkarajalista>, <Datalista>) -komennolla.

f = Frekvenssi(luokat, etlista) f = {17, 7, 4, 9, 2, 7, 8, 8, 6, 15, 17}

Frekvenssien arvot saa näkymään histogrammina Histogrammi(<Luokkarajalista>, <Korkeuslista>) -komennolla. Muutetaan arvot suhteelliseksi jakamalle ne luvulla n. Jotta pylväät näkyisivät nätisti, kerrotaan ne vielä luvulla 10. Nythän histogrammimonikulmion alaksi tuli 1! Miksi? Hannu Mäkiö laski tiheysfunktiolle sievän muodon.

histo = Histogrammi(luokat, 10 f / n) tih(x) = Jos(0.5 ≤ x ≤ 1.5, (2x) / (π sqrt(1 − (5 / 4 − x²)²)))

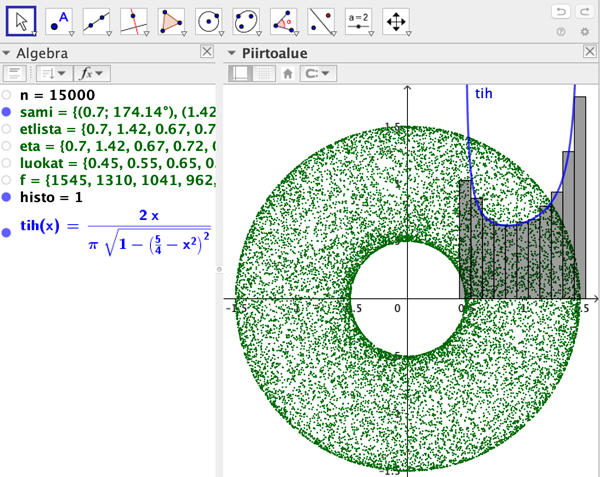
Jätän lukijalle tämän tehtävän muokkaamisen kolmiulotteisen sammakon tapaukseen.

Brute force

Raa’an voiman eli Brute force -menetelmässä käytetään tietokoneen laskentatehoa numeeristen ongelmien ratkaisussa. Simo Kivelä vertaili blogikirjoituksessaan vuoden 1960 ylioppilastehtävän ratkaisemista erilaisilla ohjelmallisilla työkaluilla. Ratkaistaan GeoGebralla tehtävä: ”Laske kaikkien niiden positiivisten kolminumeroisten kokonaislukujen summa, jotka eivät ole jaollisia 9:llä eivätkä 11:llä.”.

Ratkaisussa tarvitaan hieman Boolen logiikkaa ja jaollisuusoppia. Komento Jakojäännös(<Jaettava>, <Jakaja>) antaa tulokseksi jakojäännöksen. Totuusehto ”ja” merkitään GeoGebrassa joko && tai ∧ ja ”erisuuruus” != tai ≠. Niinpä saamme CAS:issa seuraavat totuudet eri luvuilla.

(Jakojäännös(99, 11)!=0)&&(Jakojäännös(99, 9)!=0) → false

Jakojäännös(22, 11) ≠ 0 ∧ Jakojäännös(22, 9) ≠ 0 → false

Jakojäännös(13, 11) ≠ 0 ∧ Jakojäännös(13, 9) ≠ 0 → true

Jos(<Ehto>, <Niin>, <Muuten>) -komento suorittaa Niin-kohdalla olevan komennon, mikäli Ehto on tosi, muutoin suoritetaan Muuten-vaihtoehto. Muuten syötteen voi myös jättää pois. Toki tällöin tulosteeseen tullee määrittelemättömiä ”?” olioita. Luodaan lista yo, jossa on tehtävän annon luvut.

yo = Jono(Jos((Jakojäännös(n, 11)!=0)&&(Jakojäännös(n, 9)!=0),n,0), n, 100, 999)

yo = {100, 101, 102, 103, 104, 105, 106, 107, 0, 109, 0, …, 998, 0}

Summan saa laskettua myös Summa-komennolla, sen avulla olisi voinut laskea lukujen summan ilman Jono-komentoa.

Summa(yo) a = 399996

Summa(Jos(Jakojäännös(n, 11) ≠ 0 ∧ Jakojäännös(n, 9) ≠ 0, n, 0), n, 100, 999) b = 399996

Brute force -menetelmä tuntuu meistä opettajista usein huijaukselta. Pitää muistaa, että todellisessa maailmassa on valtava määrä ongelmia, joita ei voi sievästi ratkaista koulussa opetetuilla siisteillä menetelmillä.

Tutkitaan seuraavaksi, miten Jono-komennolla saa sisäkkäisiä silmukoita. Tuotetaan kokonaislukukukoordinaatteihin pisteitä. Koska komennosta tulee aika monimutkaisen näköinen kannattaa tehdä se osissa. Luodaan ensin pisteitä vaakasuunnassa.

pisteet=Jono((i, 2), i, 1, 5)

Kopioidaan tämä komento ja kirjoitetaan sen ulkopuolelle uusi Jono-komento, sijoitetaan sen ensimmäiseksi muuttujaksi kopioitu lauseke ja muutetaan pisteen y-koordinaatti.

pisteet2 = Jono(Jono((i, j), i, 1, 5), j, 2, 4)

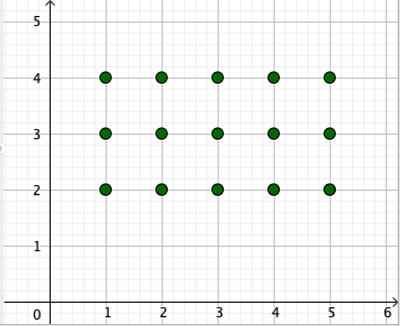
Jätän lukijalle tehtäväksi tuottaa suorakulmaisen särmiön pisteistön kolmiulotteiseen avaruuteen tällä menetelmällä.

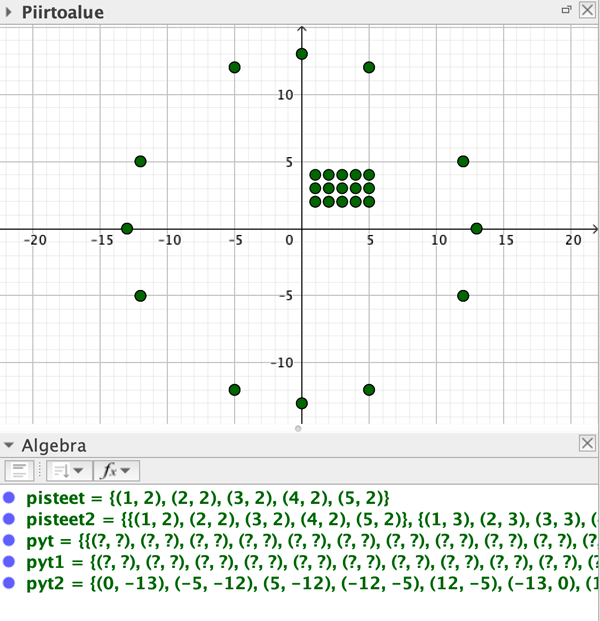
Tuotetaan seuraavaksi Pythagoraan kolmioita eli yhtälön x² + y² = z² kokonaislukuratkaisuja z:n arvolla 13. Tälle ongelmalle löytyy useita eri ratkaisumenetelmiä. Käytetään brute force -menetelmää sen kummemmin yrittämättä optimoida koodia. Käydään läpi kaikki arvot neliössä, jonka kärkien koordinaatit ovat (−13, −13), (−13, 13), (13, 13) ja (13, −13). Ehtolausekkeessa tarvittava ”yhtäsuuruus” -ehto näppäillään = = tai ≟.

pyt = Jono(Jono(Jos((i² + j²) = = 169, (i, j)), i, −13, 13), j, −13, 13)

Komento tuottaa listaan paljon määrittelemättömiä (?, ?) -pisteitä ja sisäkkäisiä kaarisulkeita. Kaarisukeista pääse eroon Tiivistä-komennolla ja määrittelemättömistä pisteistä PoistaMäärittelemätön-komennolla.

pyt1 = Tiivistä(pyt) pyt2 = PoistaMäärittelemätön(pyt1)

Yhdellä rivillä koodi olisi aina haastavaa lukea:

pyt3 = PoistaMäärittelemätön(Tiivistä(Jono(Jono(Jos(i² + j² ≟169, (i, j)), i, −13, 13), j, −13, 13)))

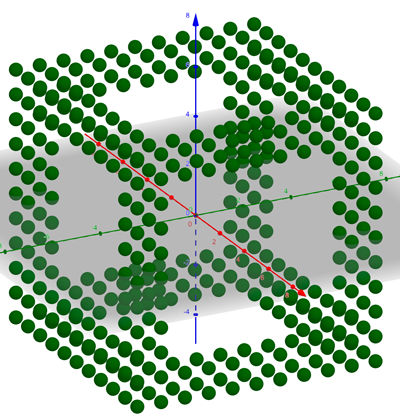
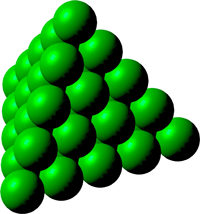
Jätän tämänkin ongelman yleistyksen 3D avaruuteen lukijalle kotitehtäväksi. Samalla kehotan kokeilemaan miten kuvan reikäinen kuutio tai marmelaadipyramidi on tuotettu. Voit myös pohtia mitä komento

janat = Jono(Jana((1, 0), Kärkipiste(Monikulmio((1; (360°) / n), (1; 2(360°) / n), n), m)), m, 1, n − 1, 1)

tekee, kun luonnollinen luku n > m > 1 ja miksi Tulo(janat) on yhtä suuri kuin n. Komento Kärkipiste(Monikulmio, i) tuottaa monikulmion i:nen kärkipisteen.