Murtolukujen visualisointia Polypad-ohjelmalla
Polypad-ohjelma (https://polypad.amplify.com/)on selaimessa toimiva ympäristö matematiikan monipuoliseen havainnollistamiseen. Polypad -ohjelma on jo aikaisemmin esitelty Dimensiossa (Amplify Polypad: Yhtälön ratkaisun visualisointia yhtälövaa’an avulla 25.4.2024) jolloin esitettiin, kuinka Polypad-ohjelmalla voidaan havainnollistaa yhtälön ratkaisua. Mutta ohjelmasta löytyy monta muutakin mielenkiintoista työkalua.
Keskitymme tässä artikkelissa murtolukujen ja niiden välisten laskutoimitusten visualisointiin Polypad-ympäristössä. Murtoluvun visuaalinen malli antaa konkreettisen kokemuksen, kuinka murtolukuja voidaan käsitellä. Tavoitteena on luoda parempaa ymmärrystä ja käsitteen muodostamista murtoluvuista ja niiden välisistä laskutoimituksista. Aluksi asetamme tavoitteen, kuinka seuraavat murtoluvut ja niiden väliset laskutoimitukset voitaisiin esittää Polypadin murtolukupalojen avulla.
Tehtävät
- Miten esitetään murtoluvut $\frac{3}{4}$ ja $\frac{4}{3}$ visuaalisesti murtolukupalojen avulla?
- Esitä murtopalojen avulla, kumpi on suurempi $\frac{1}{3}$ vai $\frac{1}{4}$?
- Esitä murtopalojen avulla, kumpi on suurempi $\frac{4}{5}$ vai $\frac{3}{4}$?
- Esitä murtopalojen avulla yhteenlasku $\frac{3}{4}$+$\frac{3}{6}$
- Esitä murtopalojen avulla kertolaskut $2\cdot\frac{2}{3}$ ja $\frac{3}{5}\cdot\frac{3}{4}$
- Esitä murtopalojen avulla jakolaskut $\frac{1}{2}:4$ ja $2:\frac{1}{4}$
- Esitä murtopalojen avulla jakolasku $\frac{2}{5}:\frac{3}{4}$.
Näytän Polypad-ohjelman visuaalisen mallin jokaisen kohtaan ja lisäksi kerron, kuinka se on saatu aikaiseksi.
Murtolukujen esittäminen
Murtolukupalat löytyvät kohdasta Fractions | Bars. Kun haluat esittää murtoluvun $\frac{3}{4}$, niin tartu hiirellä neljäsosapaloihin ja raahaa se työpöydälle. Palkki aluksi esittää yhtä kokonaista eli $\frac{4}{4}$ palkkia. Tarttumalla hiirellä palkin alareunassa olevaan kolmionmuotoiseen kahvaan ja liikuttelemalla sitä yhden pykälän vasemmalle saat aikaiseksi palkin, joka esittää murtolukua $\frac{3}{4}$. Kolmionmuotoisella kahvalla valitaan neljäsosapalojen lukumäärä. Jos haluat piilottaa valitsematta jääneen $\frac{1}{4}$ palan, niin silloin tartu puoliympyrän mukaiseen kahvaan ja siirrä myös sitä yksi pykälä vasemmalle.
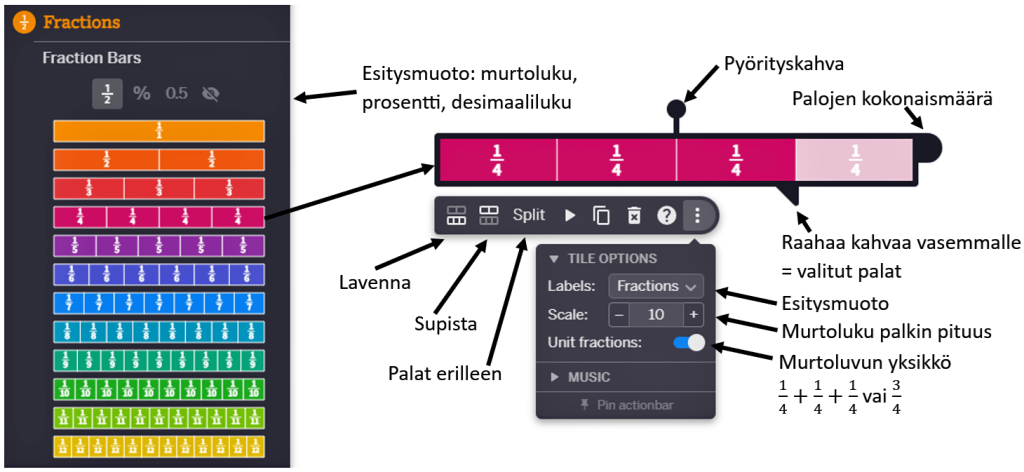
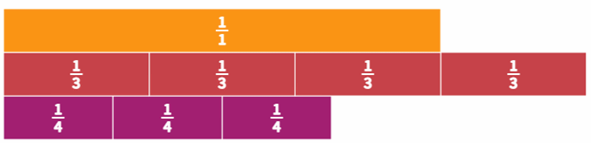
Vastaavalla tavalla raahaa ensin kolmasosapalkki työpöydälle. Mutta siirrä nyt puoliympyrän muotoista kahvaa oikealle, jolloin saat aikaiseksi $\frac{4}{3}$ -palkin. Näin saadut $\frac{3}{4}$ ja $\frac{4}{3}$ -palkit kannattaa laittaa vierekkäin, jotta niiden kokoa voi vertailla keskenään. Yleensä vertailuun mukaan kannattaa lisätä yksi kokonainen eli $\frac{1}{1}$ -palkki. Mitä havaintoja tästä voidaan tehdä? Havaitaan esimerkiksi se, että $\frac{1}{3}$ -pala on suurempi kuin $\frac{1}{4}$ -pala. Tästä päästään samalla miettimään, että nimittäjä kertoo palan koon eli kuinka moneen osaan yksi kokonainen on jaoteltu. Osoittaja taas kertoo valittujen murtolukupalojen lukumäärän eli $\frac{3}{4}$ siis tarkoittaa, että neljäsosapaloja on valittu kolme. $\frac{4}{3}$ tarkoittaa, että kolmasosapaloja on valittu neljä. Koska paloja on nyt yli yhden kokonaisen, niin samalla päästää murtoluvun esittämiseen sekalukuna $\frac{4}{3}=1\frac{1}{3}$.
Jos menet lisäasetuksiin (kolme pistettä = more tools) ja poistat valinnan kohdasta Unit fractions, niin palkit voidaan esittää myös murtolukumuodossa eli seuraavasti:
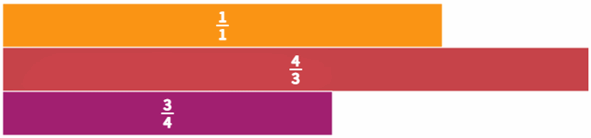
Nyt olemme saaneet esitettyä tehtävät 1 ja 2. Voit myös kokeilla esittää murtolukuja murtokakkuina (Fraction Circles).
Laventaminen
Jos verrataan kahta erinimistä murtolukua keskenään, päästään murtolukujen laventamiseen. Mitä murtolukujen laventaminen tarkoittaa käytännössä? Piirrä aluksi $\frac{4}{5}$ -palkki ja $\frac{3}{4}$ -palkki murtolukupalkkeina. Matemaattisesti ajateltuna laventaminen on kertomista, jolloin viidesosa- ja neljäsosa-palkit muutetaan kahdeskymmenesosa-palkeiksi. Kun olet piirtänyt $\frac{4}{5}$ palkin, niin tee siitä kopio ja paina työkaluvalikosta löytyvää Lavenna-painiketta, jolloin viidesosat muuttuvat ensin kymmenesosiksi. Kun painat uudestaan Lavenna-painiketta, niin kymmenesosat muuttuvat seuraavaksi viidestoistaosiksi eli tarvitsee vielä kerran painaa Lavenna-painiketta, ennen kuin saat aikaiseksi kahdeskymmenesosat. Samalla tavalla lavenna $\frac{3}{4}$ palkki kahdeskymmenesosiksi.
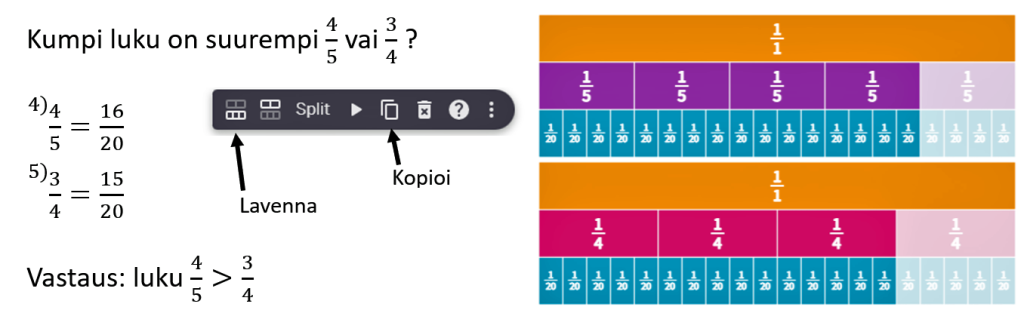
Kun palkit laittaa rinnakkain, niin nähdään, että laventaessa palojen koko pienenee, mutta toisaalta pienempiä paloja tarvitaan enemmän, jotta saadaan kuvattua sama luku. Siksi kertominen tehdään sekä osoittajaan että nimittäjään. Kun murtolukupalojen koko on nyt sama molemmilla luvuilla, suurempi luku selviää palojen lukumääriä eli osoittajaa vertailemalla. Matemaattisen merkinnän ja selittävän kuvion yhteys on selvä. Laventamista tarvitaan, kun summataan kaksi erinimistä murtolukua keskenään. Tehdään seuraava laskutoimitus ja havainnollistetaan laskun välivaiheita murtolukupalkkeina.
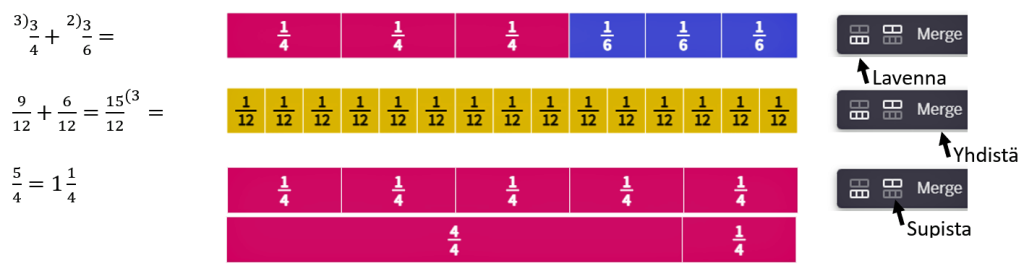
Kuten huomataan, murtopalkeilla on helppo kuvata lukujen laventaminen, summaaminen ja supistaminen. Polypadin työkaluilla on helppo kopioida palkkeja, jolloin laskun välivaiheet saadaan helposti näkyviin erilaisina palkkeina. Työkaluista löytyvät valmiit komennot laventamiselle ja supistamiselle. Lisäksi palkkeja voi pilkkoa osiin (Split) ja osia voi yhdistää isommiksi kokonaisuuksiksi (Merge), kuten esimerkiksi kokonaisluvuiksi. Murtolukupalkkien piirtäminen ja muokkaus on nopeaa. Olemme nyt tehneet tehtävät 3 ja 4.
Murtolukujen kertolasku
Aloitetaan ensin tapauksesta, jossa murtoluku kerrotaan kokonaisluvulla. Kokonaisluku kertoo, kuinka monta kappaletta murtolukuja on eli kertolasku on helppo muuttaa yhteenlaskuksi.
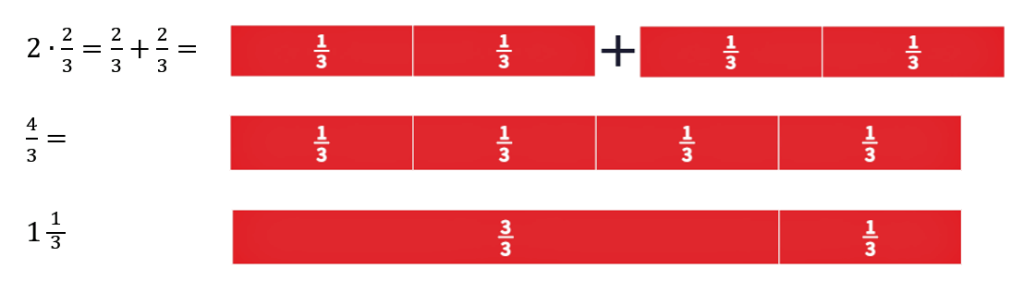
Tärkeintä tässä on huomata, että kun kerrotaan kahdella murtoluku, kertominen tapahtuu vain osoittajalle, ei nimittäjälle. Kolmasosapaloja on 2∙2 = 4 kappaletta. Palojen koko eli nimittäjä ei muutu, kun murtoluku kerrotaan kokonaisluvulla. Ainoastaan palojen lukumäärä muuttuu. Tämä kertolasku helposti sotketaan laventamiseen, mutta laventaminen on palojen jakamista pienempiin osiin, joka on siis ihan eri asia, kuin murtoluvun kertominen kokonaisluvulla. Tämä ero saadaan helposti havainnollistettua murtolukupalojen avulla.
Kerrotaan seuraavaksi kaksi murtolukua keskenään, jolloin saadaan:
$$\frac{3}{5}\cdot\frac{3}{4}=\frac{9}{20}$$
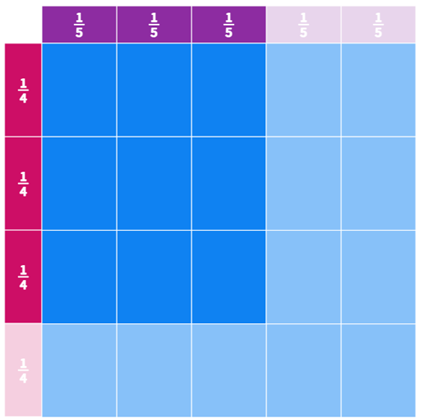
Voidaan myös ajatella, että kertolasku on sama asia kuin suorakulmion pinta-alan laskeminen. Piirretään murtolukupalkkien avulla seuraavaksi pinta-alakuvio, jossa suorakulmion kanta on $\frac{3}{5}$ ja korkeus on $\frac{3}{4}$. Piirtämiseen tarvitaan kaksi murtolukupalkkia. Piirrä aluksi molemmat murtolukupalkit, mutta pyöräytä $\frac{3}{4}$ -palkki pystyyn ja nosta palkkien nurkat kiinni toisiinsa. Pinta-ala voidaan piirtää suorakulmiotyökalulla (Geometry | Polygons and Shapes | Rectangle). Jotta suorakulmiosta tulisi oikean kokoinen, niin voit ensin rajata alueen viivatyökalulla oikean kokoiseksi. Kun piirrät suorakulmion, niin sen koko napsahtaa oikeaksi, kun suorakulmio kohtaa reunaviivan.
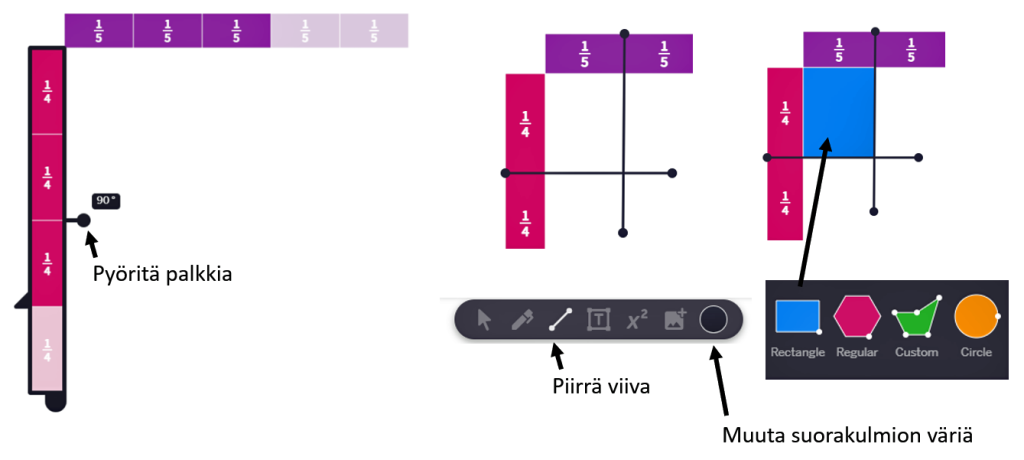
Kun olet saanut ensimmäisen suorakulmion piirrettyä, poista apuviivat. Seuraavaksi tee kopioita suorakulmiosta ja nosta suorakulmiot oikeille paikoilleen. Muuta tarvittaessa suorakulmion väri haaleammaksi, jos suorakulmio ei kuvaa haluttua pinta-alaa. Lopputuloksena sinulla pitäisi olla seuraavanlainen kuvio, josta on helppo päätellä murtolukujen kertolaskun ja pinta-ala kuvion välinen yhteys. Yhden kokonaisen palojen määrä on 4 ∙ 5 = 20, joista valitaan yhdeksän palaa kuvaamaan valittua pinta-alaa. Olemme saaneet viidennen tehtävän tehtyä.
Murtolukujen jakolasku
Mietitään vielä lopuksi murtolukujen jakolaskun havainnollistamista. Aloitetaan helposta tapauksesta, jossa murtoluku jaetaan kokonaisluvulla.
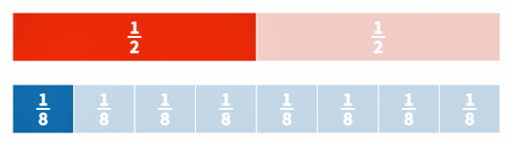
$$\frac{1}{2}:4=\frac{1}{2}:\frac{4}{1}=\frac{1}{2}\cdot\frac{1}{4}=\frac{1}{8}$$
Tämä on helppo havainnollistaa siten, että piirretään ensin $\frac{1}{2}$ -palkki, joka jaetaan neljään osaa. Tämä on sama asia kuin yksi kokonainen jaetaan kahdeksaan osaan. Vastaus on helppo nähdä kuvasta.
Jaetaan seuraavaksi kokonaisluku murtoluvulla.
$$2:\frac{1}{4}=\frac{2}{1}:\frac{1}{4}=\frac{2}{1}\cdot\frac{4}{1}=8$$
Tässä yhteydessä voi kysyä, kuinka monta neljäsosapalkkia mahtuu kahteen kokonaiseen. Kuvasta on helppo havaita, että neljäsosapalkkeja mahtuu kahteen kokonaiseen kahdeksan kappaletta.

Entä kuinka kahden murtoluvun jakolaskua voitaisiin havainnollistaa murtolukupalkkien avulla? Tehdään seuraava jakolasku.
$$\frac{2}{5}:\frac{3}{4}=\frac{2}{5}\cdot\frac{4}{3}=\frac{8}{15}$$
Piirretään aluksi molemmat palkit allekkain. Kysymys kuuluu, että kuinka monta kaksi viidesosaa -palkkia mahtuu kolme neljäsosaa -palkkiin? Kolme neljäsosaa on tässä vertailuluku, joka vastaa periaatteessa nyt yhtä kokonaista. Laskutoimituksen vastausta on kuviosta vaikea nähdä.

Jos vastauksen haluaa selvittää kuvion avulla, niin palkit pitää ensin laventaa samannimisiksi. Vertailu onnistuu vain, jos molemmissa kuvioissa on murtoluku, joilla on sama nimittäjä. Tämä idea voidaan myös havainnollistaa laskemalla.
$$\frac{2}{5}:\frac{3}{4}=\frac{8}{20}:\frac{15}{20}=\frac{8}{20}\cdot\frac{20}{15}=\frac{8}{15}$$
Koska molemmista murtoluvuista tuli nyt 20-osia, niin 20-osat supistuvat pois muutettaessa jälkimmäinen murtoluku kertolaskuksi käänteisluvun avulla. Tällöin vertaamme vain murtolukupalojen lukumäärää keskenään ja vastaus on selvästi nyt havaittavissa kuvasta. Kahdeksan kappaletta murtolukupaloja mahtuu siis 15 kappaleeseen murtolukupaloja, joka on myös jakolaskun vastaus.

Tämä idea toimii kaikkien murtolukujen jakolaskun kesken eli myös sekalukujen. Olemme saaneet havainnollistettua murtolukujen kaikki peruslaskutoimitukset murtolukupalojen avulla. Murtolukujen piirtäminen luo konkretiaa ja auttaa oppilasta ymmärtämään matemaattisen merkinnän ja visuaalisen kuvan välisen yhteyden. Polypad-ohjelma antaa mahdollisuuden havainnollistaa nopeasti murtolukuja ja niiden välisiä laskutoimituksia, jolloin kirjan tehtävät heräävät eloon. Aluksi kuvia kannattaa käyttää oppimisen tukena, jotta ymmärrys murtolukujen laskemisesta tulisi oppilaalle näkyväksi ja konkreettiseksi käsitellä. Sitten ei enää tarvita kuin riittävä määrä toistoja.
Lue myös Dimension aikaisempi artikkeli aiheesta: Murtoluvulla jakamisen malleja (22.10.2020) ja Polypad-ohjelmasta kertova Amplify Polypad: Yhtälön ratkaisun visualisointia yhtälövaa’an avulla (25.4.2024).
Tilaa Dimension uutiskirje – saat sähköpostiisi aina kuunvaihteessa koosteen tuoreimmista artikkeleista