Mitä on x + x2?

Polynomialgebrassa voidaan laskea yhteen vain samanmuotoisia termejä. Termien x ja x² asteluku ei ole sama, joten niitä ei voi yhdistää. Vielä pahempi ongelma on suurelaskennassa, sillä merkintä x + x² ei ole siellä edes järkevä. Matematiikka on kuitenkin monimuotoista. Se ei suinkaan ole vain yhden oikean ja väärän vastauksen tiede niin kuin moni uskoo kouluopetuksen perusteella. Aina yhteenlaskulle ei ole esteitä.

Nykyinen tapa nimetä muuttujia ja kirjoittaa niiden potensseja on peräisin René Descartes’in pienestä julkaisusta La Geométrie [1]. Hän ei halunnut liittää toiseen ja kolmanteen potenssiin niitä neliön ja kuution geometrisia merkityksiä, joita pidämme luonnollisina, ehkä aivan väistämättöminä.

Hänelle lauseke

$x+x^2$

oli vain tapa merkitä lyhyesti janaa, joka muodostuu kahdesta muusta janasta. Näin Descartes pystyi käsittelemään geometriaa piirtämättä kuvia. Yhteenlaskun teki mahdolliseksi se, että muuttujan toinen potenssi ei ollut hänelle geometrinen neliö, vaan janojen 1 ja $x$ kolmas verto verrannon

$\frac{1}{x}=\frac{x}{x^2}$

mukaisesti. Se edusti siis hänen ajattelussaan tietynpituista janaa eikä neliötä (kuva 1). Millaisesta verrannosta saadaan muuttujan $x$ kolmas potenssi $x^3$?

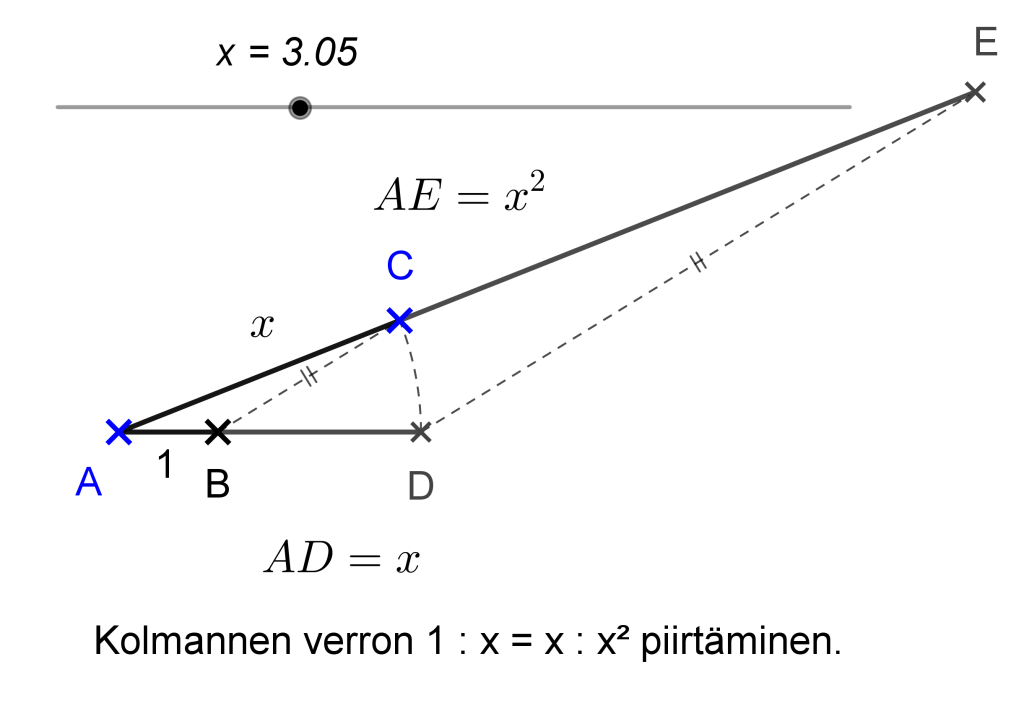
Merkinnällä $x^2$ Descartes tarkoitti janaa, jonka pituus oli $x$:n pituuden neliö. Se saatiin klassiseen tapaan piirtämällä eikä laskemalla.
(Dynaaminen matletti osoitteessa https://www.geogebra.org/m/qbf76jdz.)

Descartesin aikana tämä oli mullistava ajatus, sillä Kreikan matematiikan kulta-ajasta lähtien neliöllä ja kuutiolla oli tarkoitettu nimenomaan geometrisia objekteja. Niin ollen janan $x$ ja neliön (pinta-alan) $x^2$ laskeminen ei käynyt päinsä. Ne eivät olleet samaan lajia, teknisesti sanottuna yhteismitallisia.  Descartes’in tapaan ajatellen ne olivat kuitenkin samaa lajia eikä niiden yhteenlaskulle siten ollut estettä. Se kävi helposti piirtämällä janat $x$ ja $x^2$ samalle suoralle peräkkäin.

Descartes selitti ajatustaan näin: ”Pitää huomata, että merkinnöillä $a^2$, $a^3$ ja muilla vastaavilla tarkoitan tavallisesti vain janoja, joita kyllä nimitän neliöiksi, kuutioiksi jne, jotta voisin käyttää algebrassa tavanomaisia ilmaisuja.” Tekstin kommentaarissa [1, s. 5, alaviite 6] asiaa selitetään tarkemmin: ”Siihen aikaan, kun tämä kirjoitettiin, merkinnällä $a^2$ ei ollut tätä merkitystä, vaan sillä tarkoitettiin neliötä, joka sivu on $a$, vastaavasti $a^3$ tarkoitti kuutiota, jonka särmä on $a$.”

Antiikin kreikkalaiset olivat ajautuneet suuriin ongelmiin yhteismitattomuuden kanssa. Ei riittänyt, että yksiulotteisen pituuden ja kaksiulotteisen pinta-alan laskeminen yhteen ei käynyt päinsä. Myös luvut voivat olla yhteismitattomia, kuten esimerkiksi neliön sivu ja lävistäjä. Jos sivun pituus on 1, niin lävistäjä on $\sqrt{2}$. Niitä ei voi laskea yhteen, vaan merkitään vain $1+\sqrt{2}$. Yhteismitattomuuden syynä on tässä se, että $\sqrt{2}$ on irrationaaliluku, mikä tarkoittaa sitä, että se ei ole esitettävissä murtolukuna. Kaksi murtolukua (eli rationaalilukua) voidaan laskea yhteen ja joskus myös kaksi irrationaalilukua, kuten esimerkiksi $\sqrt{3}$ ja $2\sqrt{3}$, mutta rationaalilukua ja irrationaalilukua ei.

Yhteismitattomuuden havaitsemista on sanottu yhdeksi hämmästyttävimmistä ja kauaskantoisimmista antiikin Kreikan matematiikan alkuaikojen aikaansaannoksista [2]. Se vei pohjan pois siltä kauniilta uskolta, että ”kaikki asiat ovat lukuja”. Sen jälkeen matematiikan painopiste siirtyi geometriaan, kun aikaisemmin laskemalla ratkaistuja ongelmia, esimerkiksi toisen asteen yhtälöä vastaavia tehtäviä, ruvettiin ratkaisemaan ja ratkaistiin vielä uudelle ajalle asti geometrian avulla piirtämällä [3].

Descartes’ille lukujen maailma (algebra) ja geometria eivät sitä vastoin olleet erillisiä. Toinen esimerkki hänen yhtenäistävästä ajattelustaan oli geometristen kuvioiden ja käyrien esittämien lukujen avulla koordinaatistossa. Tämän analyyttiseen geometriaan johtaneen idean hän toi myös esille samassa julkaisussa.

Polynomialgebrassa $x$ ja $x^2$ ovat yhteismitattomia eivätkä siis yhteenlaskettavissa. Samoin on suurelaskennassa. Siellä asia voidaan kieltää sanomalla abstraktisti, että fysikaalisten suureiden summa on operationaalisesti hyvin määritelty vain silloin, kun suureet ovat yhteismitalliset. Konkreettisesti tämä näkyy siinä, että suureen ja sen neliön yksiköt eivät ole samat, kuten esimerkiksi metri ja neliömetri.

Koulumatematiikassa noudatetaan polynomialgebran ja suurelaskennan ajattelumallia tiukasti. Polynomien kohdalla summan $x+x^2$ merkitseminen on vielä sallittu, vaikka yhteenlaskua ei voidakaan suorittaa, mutta suurelaskennassa jo merkintäkin on mieletön. Descartesín geometrisessa ajattelussa yhteenlasku oli kuitenkin mahdollinen, koska myös neliö $x^2$ edusti hänelle janaa. Yhteenlaskun tuloksena oli jana, joka pituus on sama kuin janojen $x$ ja $x^2$ pituuksien summa.

Lisää luettavaa:

[1]     Descartes, R. La Geométrie. Ilmestyi 1637 kirjan Discourse de la méthode liitteenä.

Ranskankielinen alkuperäisteos ja englanninkielinen käännös, Dover 1954, saatavissa osoitteesta

https://filosofia.fi/node/7308.

[2]     Fritz, Kurt v. The Discovery of Incommensurability by Hippasus of Metapontum.  Annals of  Mathematics, vol. 46, no 2, 1945, s. 242–265. Esikatselu saatavissa osoitteesta  https://www.jstor.org/stable/1969021?read-now=1&seq=1.

[3]     Lehtinen, M. Matematiikan historia. Matematiikkalehti Solmu https://matematiikkalehtisolmu.fi/2000/mathist/.